lek_statistika

Форму розрахунку приведених трьох індексів називають агрегатною. Такі індекси дозволяють порівнювати рівні складного явища, до складу якого входить низка різнорідних елементів.

3. Середньозважені індекси. Індекси із змінними й постійними вагами

В окремих випадках вихідні дані не дозволяють вивчити динаміку економічного явища на основі агрегатної форми індексу. Другою формою зведеного індексу є середньозважений з індивідуальних індексів. Використовують два види середніх — арифметичну та гармонічну. Вибір виду середньої ґрунтується на загальних засадах: середньозважений індекс має бути тотожним відповідному індексу агрегатної форми.

Наприклад, якщо необхідно охарактеризувати зміну екстенсивного показника в середньому по сукупності різнорідних елементів, можна використовувати середньоарифметичний зважений індекс

Iw iw x0 w0

x0 w0

де iw - індивідуальний індекс; x0 w0 - ваги.

Легко довести, що цей індекс тотожний зведеному агрегатному індексу. Замінивши iw в чисельнику на співвідношення w1 /w0 , отримаємо

Для обчислення індексу за формулою середньоарифметичною зваженою використовуємо дані таблиці 9.1

Таблиця 9.1- Зміна вартості та фізичного обсягу реалізації вугілля

Очевидно, в таблиці відсутні дані, необхідні для визначення загального індексу в агрегатній формі. Тому загальний індекс фізичного обсягу продукції визначимо за формулою

90

Тобто, кількість реалізованого рядового та збагаченого вугілля збільшилася в звітному періоді в порівнянні з базисним в середньому на 2,2%.

Середньозважений зведений індекс інтенсивного показника можна обчислити за формулою середньогармоничного індексу

Ix x1 w1

x1 w1

ix

де ix - індивідуальний або груповий індекс показника; x1w1 - ваги.

Тотожність цієї форми індексу агрегатною також доводиться простим арифметичним перетворенням.

Для обчислення зведеного індексу цін використовуємо дані таблиці 9.2.

Таблиця 9.2 - Обсяг реалізації і зміна цін на вугілля

Очевидно, вибір форми індексу в кожному випадку залежить від економічної суті показників та наявної інформації.

При вивченні явищ більш ніж за два періоди використовують ряди індексів з ланцюговою та базисною системами. Вибір системи залежить від мети дослідження. При побудові таких індексів виникає проблема вибору ваги або вимірника індексів, оскільки вони можуть бути постійними (зафіксованими на рівні одного періоду) або змінними. Найчастіше при рішенні цього питання дотримуються такого правила: індекси інтенсивних (якісних) показників визначають із змінними вагами, а індекси екстенсивних (кількісних) показників

- з постійними вимірниками.

Якщо позначити послідовність періодів символами "0", "1", "2", "3", то можна побудувати такі індексні ряди:

91

При обчисленні зведених індексів з постійними вагами (або співвимірниками) діють названі в пункті 9.1 чотири правила про взаємозв'язки між індивідуальними індексами. На зведені індекси із змінними вагами або співвимірниками ці правила не поширюються.

4. Системи взаємозалежних індексів й визначення впливу окремих чинників.

Індексний метод дозволяє оцінити вплив зміни окремих чинників на зміну результативного показника при мультиплікативній формі зв'язку, причому оцінку можна здійснити як у відносному, так й абсолютному вираженні. Це означає обчислити індекси факторних показників відповідно до системи взаємозв'язаних індексів.

У загальному вигляді всі зведені двохфакторні індекси зв'язані так:

Отже, можна визначити, на скільки відсотків змінився (збільшився або зменшився) результативний показник, у тому числі за рахунок зміни відповідно інтенсивного та екстенсивного показника.

Наприклад, для даних таблиці 9.3.

Таблиця 9.3 - Виробництво продукції та її собівартість

92

Загальні витрати на виробництво в цілому виросли на 3%, при цьому за рахунок зниження собівартості одиниці продукції вони знизилися на 1,4%, а за рахунок збільшення кількості випущеної продукції зросли на 4,5%.

За допомогою методу можна визначити також абсолютний приріст результативного показника за рахунок зміни кожного чинника. Якщо мова йде про один вид продукції, то використовують систему індивідуальних індексів.

Загальний абсолютний приріст

xw x1w1 x0 w0

Його можна розкласти по чинниках (факторах)

x x1w1 x0 w1 w1 (x1 x0 ); w x0 w1 x0 w0 x0 (w1 w0 ).

Очевидно, що при такому методі розкладання абсолютного приросту по чинниках xw дорівнюватиме x + w

Розкладання абсолютного приросту по чинниках на основі зведених індексів здійснюють аналогічно індивідуальним індексам

xw x1w1 x0 w0

у тому числі

x x1 w1 x0 w1 ; w x0 w1 x0 w0 .

За даними табл. 9.3 витрати на виробництво трьох видів продукції в поточному періоді в порівнянні з базисним виросли на 3,5 тыс.грн. (119,4 -115,9). За рахунок зниження собівартості одиниці продукції загальні витрати зменшилися на 1,7 тис. грн. (119,4 - 121,1), а за рахунок збільшення продукції – виросли на 5,2 тис. грн. (121,1 - 115,9), тобто 3,5 = (-1,7) + 5,2.

Слід враховувати, що теорія індексів не дає загального методу розкладання абсолютних відхилень узагальнювального показника по факторах, коли їх число більше двох.

5. Індекси середніх величин

Поряд зі зведеними, агрегатними індексами в статистичній практиці широко використовують індекси середніх величин (індекси середньої заробітної плати, середньої собівартості одиниці продукції тощо). При цьому середні визначаються, по-перше, на основі групових середніх, а, по-друге, по однойменній продукції, фізичний обсяг якої можна підсумовувати.

Як відомо, рівень середньої залежить від значень ознаки хj і структури сукупності:

93

де fj — частота;

dj — частка j-ї складової сукупності.

Наприклад, середня продуктивність праці робітника по видобутку по виробничому об'єднанню (холдингу) залежатиме як від продуктивності праці на окремих підприємствах, що входять в об'єднання, так і від частки їх в загальній чисельності робітників по видобутку об'єднання.

Очевидно, що й динаміка середньої визначається цими факторами: а) зміною значень ознаки xj,

б) структурними зрушеннями.

Вплив кожного з них на динаміку середньої оцінюється за допомогою системи індексів середніх величин: змінного й фіксованого складу, а також структурних зрушень.

Індексом змінного складу I x називають індекс середньої величини, він відбиває не лише зміни значень ознаки х, а й зміни в структурі сукупності:

де x0 , x1 - рівні усереднюваного показника, w0 , w1 - частоти (ваги) інтенсивного показника.

В індексі фіксованого складу I x ваги постійні, тобто усувається вплив на динаміку середньої структурних зрушень. Його величина показує, як у середньому змінилися значення ознаки при незмінній, фіксованій структурі:

Індекс структурних зрушень Id, навпаки, показує, як змінилася середня за рахунок структурних зрушень; значення ознаки x фіксуються на постійному рівні:

94

Тема 10. Аналіз інтенсивності динаміки.

1.Суть і складові елементи динамічного ряду.

2.Характеристики інтенсивності динаміки.

3.Середня абсолютна та відносна швидкість розвитку.

1. Суть і складові елементи динамічного ряду

Суспільні явища безперервно змінюються. Аналіз соціальноекономічного розвитку — одне з важливих завдань статистики. Інформаційною базою його слугують динамічні (часові, хронологічні) ряди.

Динамічний ряд — це послідовність чисел, які характеризують зміну того чи іншого соціально-економічного явища. Елементами динамічного ряду є перелік хронологічних дат (моментів) або інтервалів часу і конкретні значення відповідних статистичних показників, які називаються рівнями ряду.

При вивченні динаміки важливі не лише числові значення рівнів, а і їх послідовність. Як правило, часові інтервали між рівнями однакові (доба, декада, календарний місяць, квартал, рік). Узявши будь-який інтервал за

одиницю, послідовність рівнів записуємо так: y1 , y2 , y3 , ... , yn , де n – число рівнів (довжина динамічного ряду)

Залежно від статистичної природи показника-рівня розрізняють динамічні ряди первинні й похідні, ряди абсолютних, середніх і відносних величин. За ознакою часу динамічні ряди поділяються на інтервальні та моментні. Рівень моментного ряду фіксує стан явища на певний момент часу t, наприклад кількість працюючих на початок року, студентів — на 1 вересня і т. д. В інтервальному ряді рівень — це агрегований результат процесу й залежить від тривалості часового інтервалу (виробництво електроенергії за рік). Зауважимо, що й похідні показники, обчислені на основі інтервальних рядів, на відміну від моментних залежать від протяжності часу (середньодобове чи середньорічне виробництво електроенергії на душу населення).

Передумовою аналізу динамічних рядів є порівнянність статистичних даних, які його формують, щодо одиниць вимірювання, методології обчислення показників, території, кола об'єктів та інших позицій. Порівнянність даних забезпечується на етапах їх збирання та обробки. Використовують також спеціальні прийоми зведення даних до порівнянного вигляду — «статистичні ключі» зімкнення динамічних рядів. Припустимо, помісячні рівні витрат сировини на виробництво продукції в І півріччі непорівнянні, оскільки у квітні змінився порядок обліку витрат (див. табл. 10.1). Подолати переривчастість ряду можна двома способами. Перший — спосіб відносних рівнів, коли за базу порівняння для кожного ряду беруть квітневий рівень. Два ряди відносних рівнів об’єднуються в один.

Другий спосіб ґрунтується на співвідношенні квітневих рівнів: 55 : 50 = 1,1. Помноживши рівні першого ряду на цей коефіцієнт, дістанемо єдиний зімкнений (порівнянний) ряд динаміки за весь період (остання графа таблиці).

96

Таблиця 10.1 – Зімкнення динамічних рядів

2. Характеристики інтенсивності динаміки

Швидкість та інтенсивність розвитку різних суспільних явищ значно варіюють, що позначається на структурі відповідних динамічних рядів. Для оцінювання зазначених властивостей динаміки статистика використовує низку взаємозв’язаних характеристик. Серед них: абсолютний приріст, відносний приріст, темп зростання, інші.

Розрахунок характеристик динаміки ґрунтується на порівнянні рівнів ряду. При порівнянні певної множини послідовних рівнів база порівняння може бути постійною чи змінною. За постійну базу вибирається або початковий рівень ряду, або рівень, який уважається вихідним для розвитку явища, що вивчається. Характеристики динаміки, обчислені відносно постійної бази,

називаються базисними. Якщо кожний рівень ряду yt порівнюється з

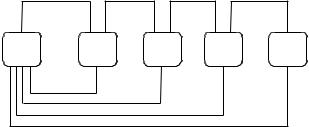
попереднім yt 1 , характеристики динаміки називаються ланцюговими. Схематично варіанти порівняння ілюструє рисунок 10.1.

Ланцюгові характеристики

Рисунок 10.1. Схеми порівняння при обчисленні ланцюгових і базисних характеристик динаміки

Абсолютний приріст t характеризує абсолютний розмір збільшення

(чи зменшення) рівня ряду yt за певний часовий інтервал і обчислюється як різниця рівнів ряду:

97

базисний приріст t yt y0 ;

ланцюговий приріст t yt yt 1 .

Знак «+», «–» свідчить про напрям динаміки.

Темп зростання kt показує, у скільки разів рівень yt більший (менший) від рівня, узятого за базу порівняння. Він являє собою кратне відношення рівнів:

Отже, при стабільному абсолютному прирості (стабільній абсолютній швидкості) темпи зростання зменшуватимуться. Стабільні темпи зростання можливі за умови прискорення абсолютної швидкості.

t

Величину yt 1 називають відносним прискоренням або темпом

приросту і позначають символом Т t . Вона функціонально пов’язана з темпом зростання, але на відміну від останнього завжди виражається в процентах:

Тt 100 kt 1 .

Отже, темп приросту показує, на скільки процентів рівень yt більший (менший) від бази порівняння.

Співвідношенням абсолютного приросту і темпу приросту визначається абсолютне значення 1% приросту. Нескладні алгебраїчні перетворення цього відношення показують, що воно становить соту частину рівня, узятого за базу

98

У таблиці 10.2 наведені всі розглянуті характеристики динаміки на прикладі виробництва умовної продукції за 3 роки. Очевидно, що ланцюгові й базисні характеристики динаміки взаємопов’язані:

а) сума ланцюгових абсолютних приростів дорівнює кінцевому базисному:

У нашому прикладі: 12 + 9 = 21 тис. нат.од.; б) добуток ланцюгових темпів зростання дорівнює кінцевому базисному:

У нашому прикладі: 1,072 · 1,051 = 1,127 або 186 : 165 = 1,127.

Щодо темпів приросту, то вони не мають таких властивостей, як абсолютні прирости чи темпи зростання. Ланцюгові й базисні темпи приросту співвідносяться через темпи зростання.

Таблиця 10.2 – Абсолютні та відносні характеристики динаміки

Якщо швидкість розвитку в межах періоду, що вивчається, неоднакова, порівнянням однойменних характеристик швидкості вимірюється прискорення чи уповільнення динаміки. На базі абсолютних приростів оцінюються

абсолютне та відносне прискорення. Абсолютне — це різниця між

прискорення обчислюється порівнянням абсолютних приростів

Обчислимо характеристики прискорення на прикладі табл. 10.2:

-t = 9 – 12 = – 3 тис. т. Знак «мінус» свідчить про уповільнення динаміки.

-темп уповільнення абсолютної швидкості: 9 : 12 = 0,75.

99