
Учебное пособие_МММТС
.pdf, -
.
.
•- ,
-
.
•- -
,
, ,
. -
-
, .
•-
, , , -
, . ,
-
, - . . -
.
•-
.
, : 1) ; 2) ( );
3) - -
.
x, ; . .
>0 = )>0 , ,
(x*) < , *
( *) < .
-. , , , -, , ,
. -
.
.
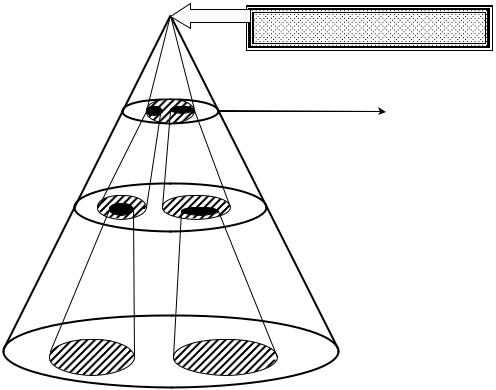
,
-
.
1.2.6.
-
, . ,
-
. -
-
. ,
. -
. -
( . 1.4). -
, .


1.4 -
, .
.
– ,
, -
.
- . , -
,
. , -
.
-
». -
.
-
, ,
. , , -
. , -
.
.
. 1.4): ; ;
.
, -
, -
, -
. , -
, , -
, .
, -
,
( .1.5.). -
, , ,
, -
.
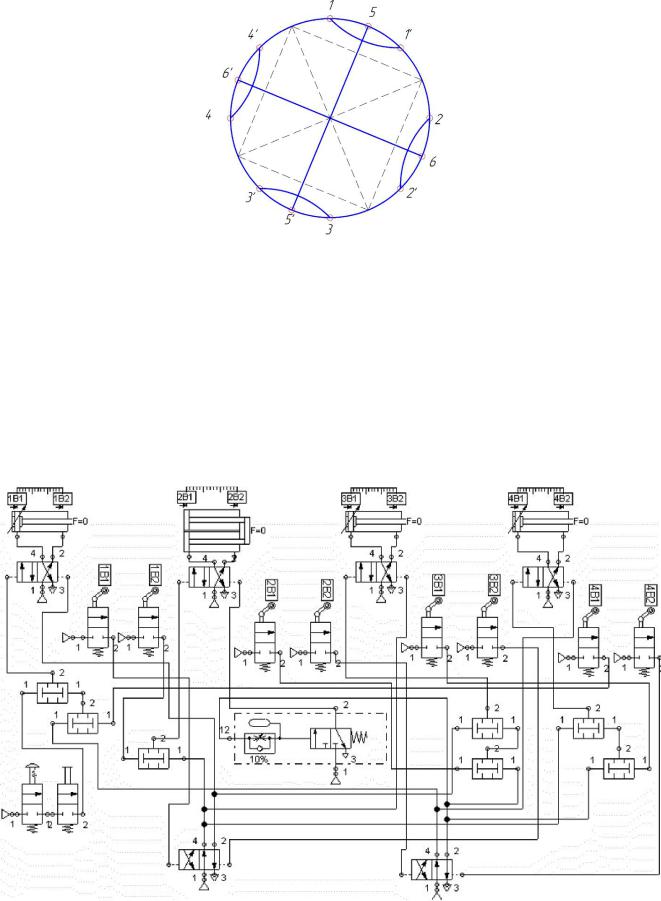
1.5 – -
.
.
. , , -
,
( .1.6),
.
1.6 -
, , -
:
m |
d 2 x |
|
( p p |
)S |
j |
|
x F |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
dt2 |
1 |
a |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dp |
|
|
|
kf1 Kp |
RT |
( 1 ) |
|
kp |
dx |
|
|
|
|||||||||
|
1 |
|
S1 (x01 x) |
|
1 |
|
|
|
|
||||||||||||
dt |
|
|
|
|
|
|
|
|
(x01 x) dt |
|
|
|
|||||||||
m |
d 2 x |
|
j (s x) ( p2 pa )S1 F |
|
|
|
|||||||||||||||
dt2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dp |
|
|
|
kf2 Kp2 |
3k 1 |
RT |
|
|
|
|
|
|
kp |
|
|
dx |
|||||
2 |
|
|
2k |
|
|
|
( |
a |
) |
2 |
|
||||||||||
dt |
|
|
|
|
|
|
|
k 1 |
|
2 |
(s x02 x) dt |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
S2 (s x02 x) p 2k |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
, ,
, -
MathCad, Matlab .
-
. -
. -
, .
:
, , |
||||||||||||||||||||||||||||||
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
( |
), |
|
|
|
|
|
|||||||||||||||||||||||
|
|
( = 1,2,3 … ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
= ( , |
, … ) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
, |
|
|
|
||||||||||||||||||||
|
, |
|
|
|
= ( |
|
|
) |
+ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
, , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
( , ), |
|
|
|
|
|
|
( , ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
; |
|
|
|
|
- |
||||||||||||||||||||||
|
|
|
; |
|
|
|
|
|
- - |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
. |
|
|
|
||||||||||||||||||||||||||
|
|
( , ) |
|
|
|
|
|
|||||||||||||||||||||||
|
|
) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
( |
|
|
|
|
( ) |
|
= |
|
) + ( , ). |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||||||
|
|
( , ) = ( ) ( , ) = ( ), |
|
|
|
|
|
|
- |
|||||||||||||||||||||
|
|
, |
|
|
: |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
) + |
|
|
|
, = . |
||||||||||||||||||||||||||||
|
= ( ). |
|
|
|
= |
= 0 |
|
|
|
|
|
|||||||||||||||||||
= 0. |
|
|
|
|
|
|
||
= 0 |
|
|
||||||
|
|
|
|
|
||||
: |
+ ( , ) |
+ = . |
, - |
|||||
|
+ |
( |
) = , |
|
||||
, -.
( , ) = ,0 :
.
[] ,
,
, , , -
,
, – ,
.
.1.7 -
, .
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|

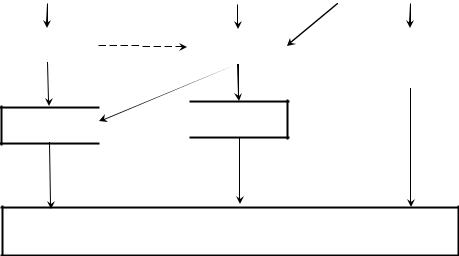
1.7 -
:
- ;
- ;
– ;
- .
, . -
, .
, -
, ,
. -
. -
-
,
. , -
-
; - .
