Тема 2. Елементи теорії границь

 

2.1. Границя послідовності та границя функції

 

Поставимо у відповідність кожному  деяке дійсне число . В цьому випадку кажуть, що задано числову послідовність (sequence, number sequence) (позначають ).

Наприклад, числовими послідовностями є: числа Фібоначчі

1, 1, 2, 3, 5, 8,…; арифметична та геометрична прогресії.

 

Означення 2.1. Число a називається границею послідовності (limit of sequence) , якщо для будь-якого як завгодно малого додатного числа  існує число  таке, що для всіх  виконується нерівність

 

 

Якщо ввести позначення:  - довільний (будь-який);  - існує, то означення 2.1 можна скорочено записати так:

 

.

 

Те, що число a є границею послідовності , записують так:

 

 або .

 

Послідовність, яка має границю, називається збіжною (convergent sequence), а яка не має границі –розбіжною (divergent sequence).

Будь-який інтервал виду , де , називається -околом точки (neighborhood of point)a на числовій осі.

З геометричної точки зору, якщо число a є границею послідовності , то в довільний -окіл точки a потраплять всі члени послідовності , окрім скінченної їх кількості (може бути як завгодно малим). Можна сказати, що члени послідовності  групуються навколо точки а.

 

Приклад 2.1. Довести за означенням, що .

Доведення. За означенням 2.1 для кожного  ми повинні вибрати номер  так, щоб при всіх  виконувалась нерівність . В нашому випадку дана нерівність набуває вигляду

.                                           (*)

Оскільки , то нерівність (*) перепишемо так , звідки . Тепер, якщо ми оберемо , то при всіх  нерівність (*) буде виконуватись, а отже число  за означенням є границею даної послідовності.

Наприклад, при вибраному  отримаємо , а це означає, що для всіх  члени  цієї послідовності потраплять в окіл

.

 

Границя функції в точці

Нехай функція  визначена на деякій множині X і точка  або . Візьмемо з Xпослідовність точок , відмінних від a, яка збігається до цього числа:

 

.                                     (2.1)

 

Значення функції  в точках послідовності (2.1) утворюють в свою чергу числову послідовність:

                             (2.2)

Означення 2.2. (за Гейне). Число b називається границею функції (limit of function)  в точці  (або при ), якщо для будь-якої збіжної до a послідовності (2.1) значень аргументу x, відмінних від a, відповідна послідовність (2.2) значень функції збігається до числа b.

Позначають це так:

 

,                                          (2.3)

або

 

.

Це означення границі функції за Гейне (мовою послідовностей), його можна записати скорочено так:

 

.

 

Приклад 2.2. Довести, що .

Доведення. За означенням 2.2: 

 

.

Ця границя не залежить від вибору послідовності , яка збігається до числа 1.

 

Означення 2.3. (за Коші). Число b називається границею функції  в точці  (або при ), якщо для будь-якого як завгодно малого числа  існує таке додатне число , що для всіх , які задовольняють нерівність , виконується нерівність

 

.

 

Скорочено це означення можна записати так:

 

.

 

З геометричної точки зору, якщо число b є границею функції  в точці , то для всіх значень аргументу , які групуються навколо точки , відповідні значення функції групуються навколо точки .

Зауваження. Можна показати, що означення 2.2 та 2.3 є еквівалентними.

 

Приклад 2.3. Довести, що .

Доведення. Застосуємо означення 2.3:

 

 (рис. 2.1).

 

, тобто .

 

Рис. 2.1

Нехай, наприклад, , тоді відповідне  і

 

.

 

Односторонні границі (one-sided limit)

Означення 2.4. Число b називається границею функції  справа (right-handed limit) [зліва (left-handed limit)] в точці , якщо для будь-якого як завгодно малого числа  існує таке додатне число , що для всіх x, які задовольняють нерівність   [], виконується нерівність

 

.

 

Скорочено означення границі справа (зліва) в точці , можна записати так:

 

.

Позначають границю справа  або ;

границю зліва -  або .

 

Для існування границі функції  в точці  необхідно і достатньо, щоб мала місце рівність

 

.

 

Границя функції на нескінченності

Означення 2.5. Число b називається границею функції  при , якщо для будь-якого як завгодно малого числа  існує таке додатне число N, що для всіх x, які задовольняють нерівність , виконується нерівність

 

.

 

Скорочено означення границі при  можна записати так:

 

.

Якщо при цьому елементи  послідовності  додатні (від’ємні), то пишуть так:

 

 

Приклад 2.4. Довести, що .

Доведення. Нехай виконується нерівність

 

,

 

,

 

звідси . І, якщо за  прийняти , то , тобто , а це за означенням 2.5 означає, що  (рис. 2.2).

 

Нехай, наприклад, ; тоді . Отже виконується

.

 

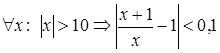Рис. 2.2