4.Формулы связи координат соответственных точек местности

и горизонтального снимка.

У горизонтального снимка угловые элементы внешнего ориентирования ===0. Будем считать, что координаты главной точки снимка x₀=y₀=0.

В этом случае

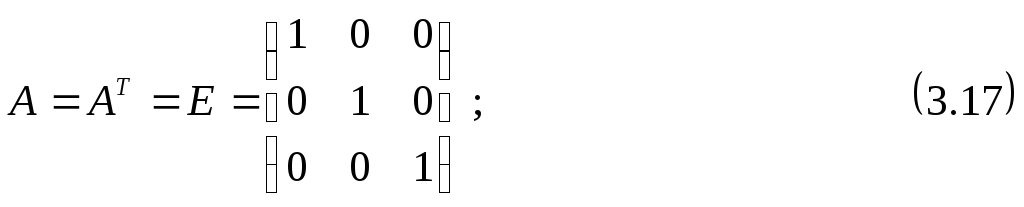
Формулы связи координат при этом будут иметь вид

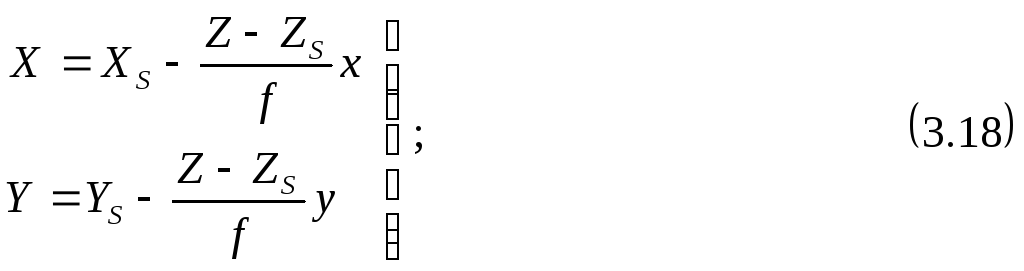
(3.19)

Если в качестве начала системы координат объекта OXYZ выбрать центр проекции S, то Xs=Ys=Zs=0, а формулы (3.18) и (3.19) примут вид:

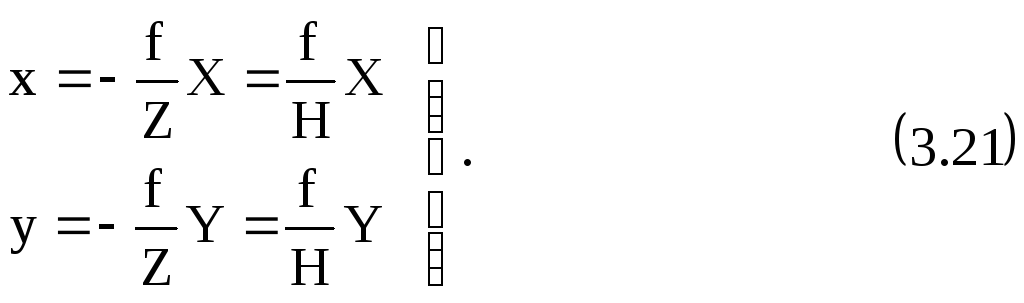
( H = -Z – высота фотографирования над определяемой точкой)

Из формул(3.20) и (3.21) следует, что горизонтальным снимком горизонтальной местности можно пользоваться как планом масштаба

.

5. Формулы связи координат соответственных точек горизонтального и наклонного снимков

Пусть из точкиS получен наклонный Р и горизонтальный Р⁰ снимки, на которых точка М объекта изобразилась соответственно в точках m и m⁰ (рис. 3.3). Найдем зависимости между координатами этих точек.

На рис. 7 и – векторы, определяющие положение точек m и m⁰ относительно центра проекции S на снимках Р и Р⁰.

Векторы коллинеарные, поэтому можно записать:

; (3.22)

где N - скаляр.

В

Рис.3.3

системе координат горизонтального снимкаSx⁰y⁰z⁰ выражение (3.22) имеет вид (полагая х⁰=у⁰=0):

Рис. 3.7

; (3.23)

где x⁰y⁰z⁰ –координаты вектора в системе координат горизонтального снимка.

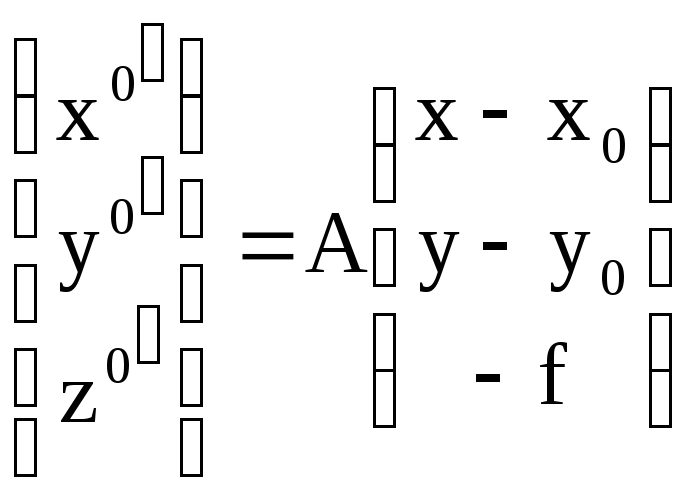; (3.24)

Из третьего уравнения (3.23) следует, что

.

Подставив значение N в первые два уравнения (3.23) получим формулы связи координат соответственных точек горизонтального и наклонного снимков:

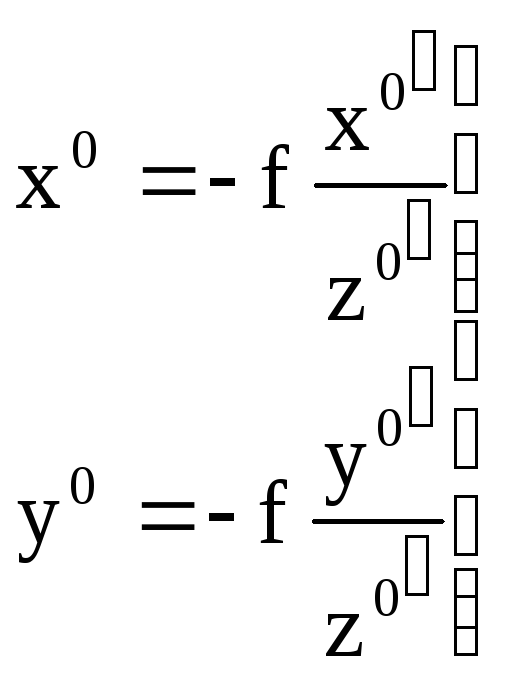; (3.25)

которые с учетом (3.24) имеют вид:

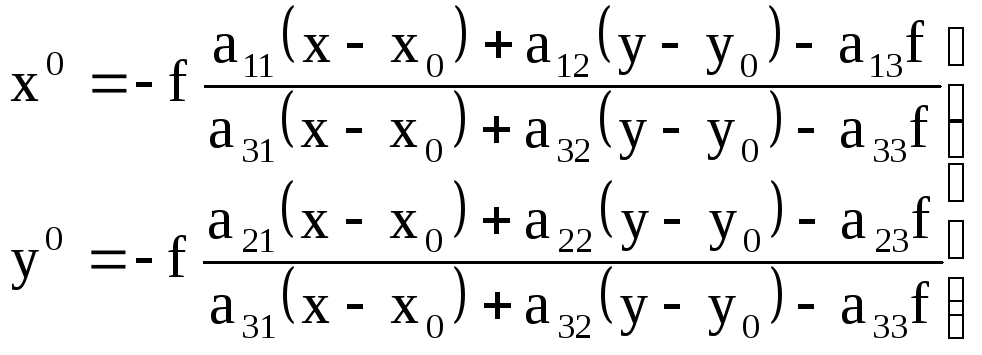. (3.26)

6. Масштаб изображения на аэроснимке

Ранее было установлено, что масштаб горизонтального снимка рав­нинной местности по­стоянен и определяется отношением фокус­ного рас­стояния съемочной камеры к высоте фотогра­фирования. На­клонный снимок со­держит перспективные искаже­ния, и его масштабуже не будет постоян­ным. В частности, из рис. 3.4 сле­дует, что

для снимка P⁰: ; для снимкаP: .

Следовательно, масштаб изображения следует опреде­лять как от­но­шение бес­ко­нечно малых отрезков наклонного снимка и мест­ности:

(3.27)

где dl и dL – бесконечно малые отрезки снимка и мест­ности, свя­зан­ные с бесконечно ма­лыми приращениями координат ограничивающих их точек следую­щи­ми за­висимо­стями (рис. 3.5):

(3.28)

Для вывода формулы, оп­ределяющей масштаб на­клон­ного снимка по про­изволь­ному направлению, ис­поль­зуются формулы связи ко­орди­нат точек снимка и местности, при выводе которых коор­динатные оси ox и OX совмещаются с главной вер­тика­лью и ее

проекцией.

После преобразований фор­мула мас­штаба снимка в точке с координатами x, y по про­из­вольному направ­лению при­мет вид

, (3.29)

где

.

Выполним анализ формулы (3.29), получим формулы мас­штаба в ос­новных точ­ках снимка по главной вертикали и по горизон­талям.

1. Снимок горизонтальный (_с= 0). Подстановка _c дает k = 1, c = 0, и вместо (3.29) будем иметь

. (3.30)

Следовательно, масштаб горизонтального снимка плоской местно­сти – величина по­сто­янная, не зависящая от положения точки.

2. Масштаб по главной вертикали (y = 0,  = 0). Под­ста­нов­ка в (3.29) дает k=cos_c и c=0. Тогда формула масштаба по глав­ной вер­тикали

. (3.31)

3. Масштаб по горизонталям ( = 90). Подкоренное вы­ра­же­ние в знамена­теле формулы (3.29) равно k, и искомый масштаб

. (3.32)

Как видно, масштаб по любой горизонтали явля­ется величиной постоянной, что и подтверждает пер­спек­тива сетки квадратов.

Действуя аналогично, можно получить формулы для расчета мас­штаба по главной верти­кали и горизонталям в основных точках.

Масштаб в точке нулевых искажений.

Подставив в (3.29)y=0,oc=x=–f(1–cos)/sin согласно(3.40),k=1, c=0, получим

. (3.33)

Масштаб в точке надира(x= – ftg, k=1/cos, c=0):

. (3.34)

Масштаб в главной точке снимка(x=0, k=cos, c=0):

. (3.35)

4. Изменение масштаба в пределах аэроснимка можно по­лу­чить, опреде­лив разность масштабов по главной вертикали в двух сим­метрично расположенных точках с абс­циссами +x и –x:

После несложных преобразований, полагая, с достаточной для при­ближенных оценок точностью, что средний масштаб аэроснимка опре­деляется по формуле (3.33):

. (3.36)

Расчеты по этой формуле показывают, что при x=f и _c=30 отно­си­тельное измене­ние масштаба составит около 1/30. С такой же точ­ностью будут определены и длины измеренных на снимке линий. Сле­дова­тельно, выполнять измерения по контактным аэроснимкам с ис­пользованием их среднего масштаба нужно весьма осто­рожно.