3.Формулы связи координат соответственных точек снимка и местности.
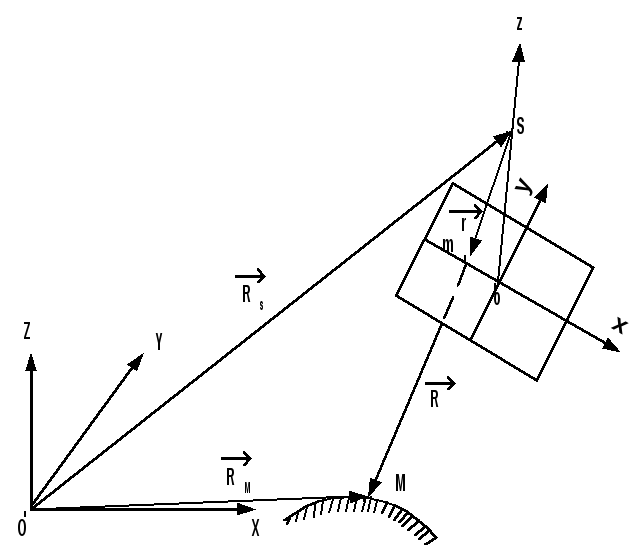
Пусть из точки S
получен снимок Р, на котором точка М
местности изобразилась в точке m.
Найдем зависимости между координатами
этих точек. Положение точки М местности
в системе координат объекта OXYZ
определяет вектор
.
Вектор
определяет положение центра проекции
S
в системе координат объекта OXYZ.
В
Рис. 3.2
и
определяют собственно положение точек
m
и М относительно центра проекции S.
Из рис.3.2 следует, что
(3.5).
Векторы
коллинеарные, поэтому можно записать,
что
;
(3.6)
где N-скалярная величина.
С учетом (3.6) выражение (3.5) имеет вид
;
(3.7)
В координатной форме выражение (3.7) имеет вид
;
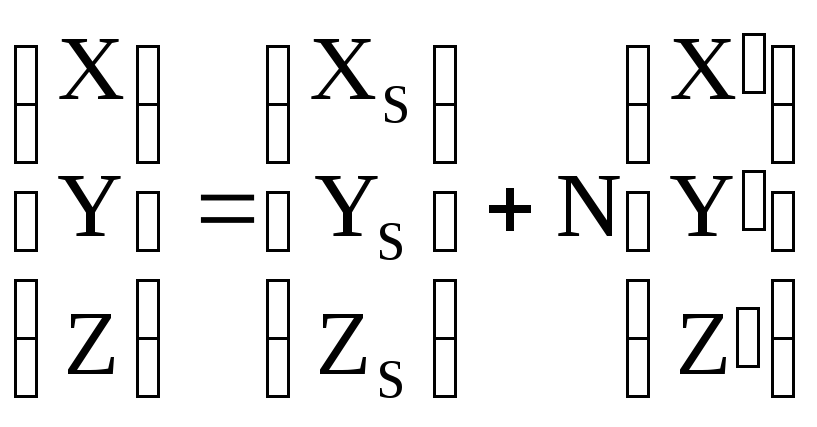или
.
(3.8)
В выражении (3.8):
X,Y,Z-координаты точки М в системе координат объекта,
координаты центра
проекции S
в системе координат объекта;
координаты
вектора
в
системе координат объекта.
;
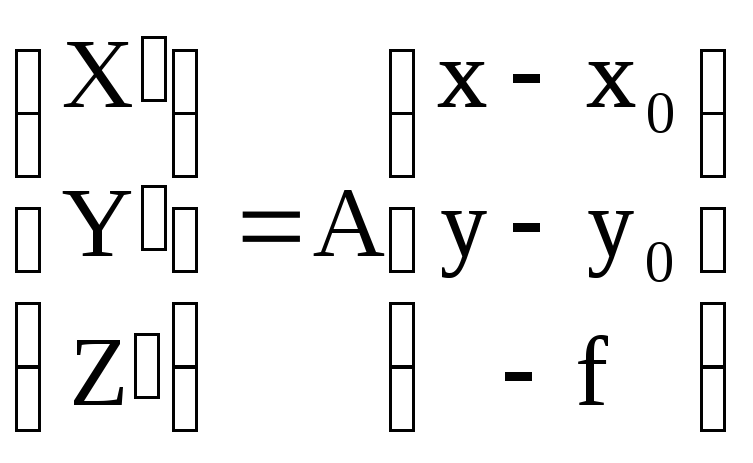(3.9)
где А-матрица преобразования координат, элементы aij которой определяются по значениям угловых элементов внешнего ориентирования снимка ,,.
Из третьей формулы выражения (3.8) следует, что
.
Подставив значение N в первые две формулы выражения (3.8) получим формулы связи координат соответственных точек местности и снимка:
;
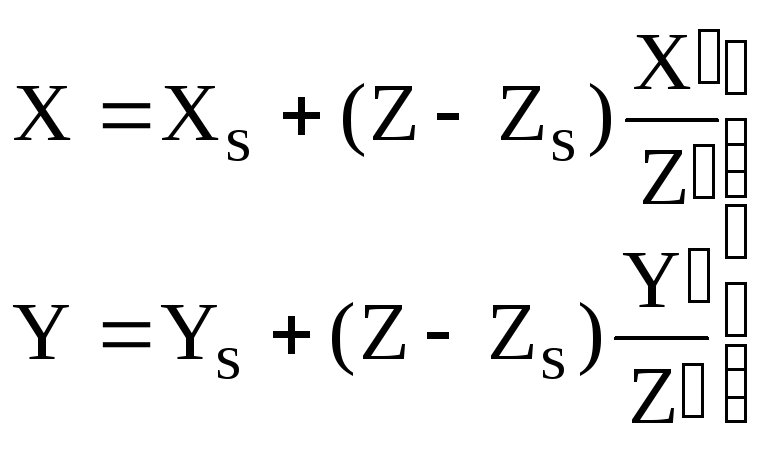(3.10)
которые с учетом (3.9) имеют вид
;
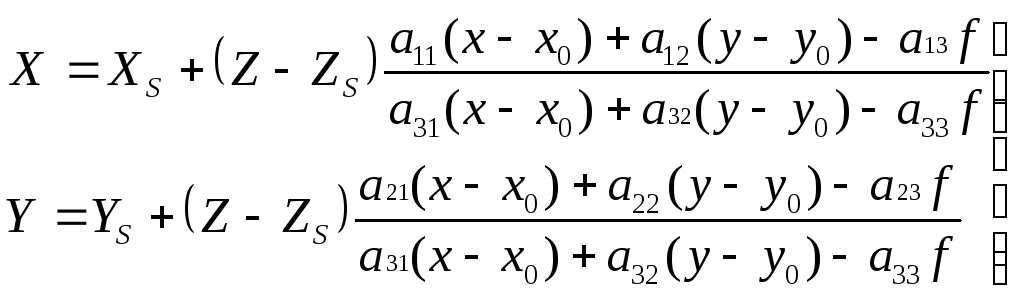(3.11)
Из формул (3.10 и 3.11) следует, что координаты точки местности по снимку можно получить по координатам её изображения на снимке, если известны элементы внутреннего и внешнего ориентирования снимков и известна высота Z этой точки.
Найдем теперь формулы связи координат соответственных точек и местности, которые позволят вычислить координаты изображения точки на снимке в системе координат снимка по координатам соответственной точки местности, определенным в системе координат объекта OXYZ.
Из выражения (3.7) следует, что
.
(3.12)
В координатной форме выражение (3.12) имеет вид
;
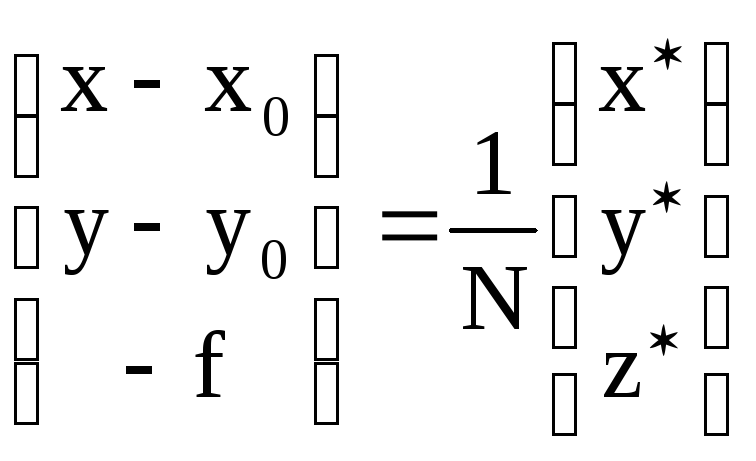или
;
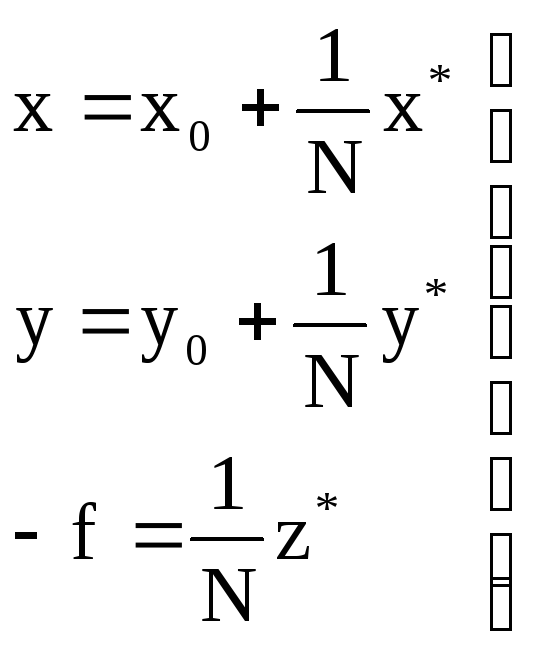(3.13)
В выражении (3.13) x,y –координаты изображения точки местности m в системе координат снимка Sxyz.
;
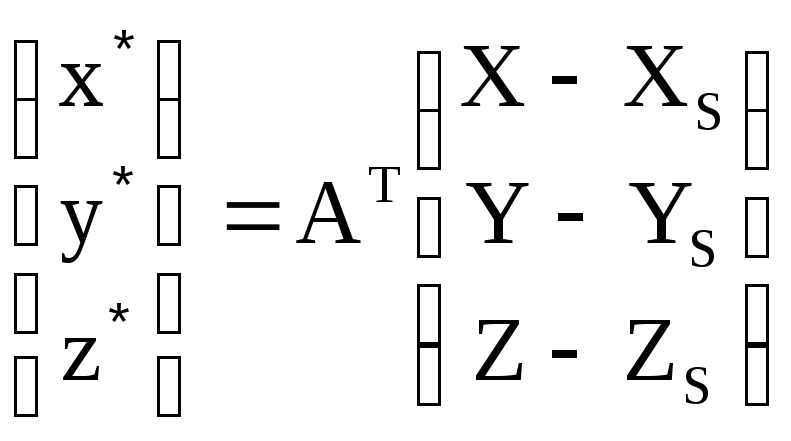(3.14)
Из третьего выражения (3.13) следует, что
.
Подставив значение
в
первые два уравнения выражения (3.9),
получим формулы связи координат
соответственных точек снимка и местности.
(3.15)
которые с учетом (3.14) имеют вид
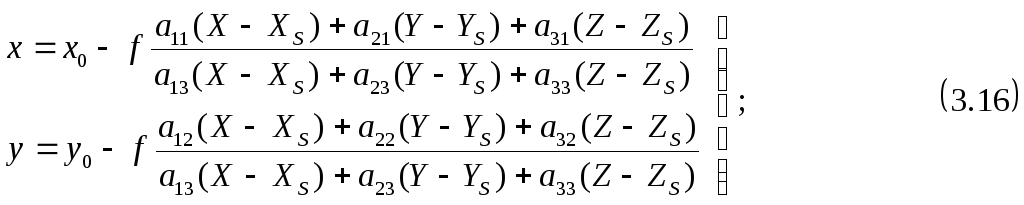
Уравнения (3.16) в фотограмметрии часто называют уравнениями коллинеарности.