
Теор. Мех. Методическое пособие для КР
.pdf
3. Найдем ускорение точки М:
|
|
|
|
|
|
|
|
|
|
&& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
; cos(w, x) = |
|
|
|
|
|
||
|
|
|
wМ = |
|
&&2 |
|
&&2 |
x |
|
||||||
|
|
|
|
|
; |
|
|
|
|
||||||
|
|
|
|
x |
+ y |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
w |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
&&x = w |
|
= 0; |
&&y = w = 2 см/с2 |
; |
w |
|
= 2 см/с2 ; |
|
|
R |
|
|
|
oy. |
|
|
|
|
|
|
|
||||||||||
X |
|
cos (w, x) = 0 / 2 = 0, w |
|
|
|
||||||||||
|
|
Y |
|
M |
|
|
|
|
M |
|
|
|
|
||
Покажем в точке М вектор ее ускорения, который в данном случае параллелен оси оу.
4. Вычислим касательное ускорение точки. Из теории естественного способа задания движения точки известно, что
R R n |
R |
τ |
|
|
|
R |
τ |
|
dv |
|
|
|
|
|
|
R n |
|
v2 |
|
|
|||||
w = w |
+ w |
; |
|
|
w |
|
= |
|
|
; |
|
|
|
|
|
w |
= |
|
|
; |
|||||
|
|
|
|
dt |
|
r |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
2t |
|
|
|
||
|
|
2 |
|
|
2 |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
w = (wτ ) |
+ (wn ) ; |
wτ = |
|
|
(2 1 |
+ t |
2 )= |
|
|
|
|
. |
|||||||||||||
|
dt |
|
|
|
|
||||||||||||||||||||
|
1 + t 2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При t = 1 с касательное ускорение равно wτ |
= |
|
|
см/с2 , оно представляет |
|||||||||||||||||||||
|
2 |
||||||||||||||||||||||||
|
|
|
|
|
R |
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|||
собою проекцию ускорения |
на касательную к траектории. В данном при- |
||||||||||||||||||||||||
wM |
|||||||||||||||||||||||||
мере это ускорение направлено по скорости.
Вычислим нормальное ускорение точки. Воспользоваться формулой
wn = v2/r
мы не можем, т. к. не знаем радиуса кривизны r траектории точки, поэтому определяем его из зависимости
wM = 
 (wMn )2 + (wMτ )2 wMn =
(wMn )2 + (wMτ )2 wMn = 
 (wM )2 - (wMτ )2
(wM )2 - (wMτ )2
при t = 1 c, wMn = 
 4 - 2 =
4 - 2 = 
 2 = 1,41 см/с2 .
2 = 1,41 см/с2 .
Нормальное ускорение всегда направлено по нормали, проведенной к траектории в данной точке, к центру кривизны.
При необходимости, зная нормальное ускорение точки и ее линейную скорость, мы можем вычислить радиус кривизны траектории.
В нашем примере
с = |
v2 |
|
rM = |
vn |
= |
8 |
|
|
= 5,64 см. |
|
|
||||
|
; |
M |
|
|
|
|
|
|
|
||||||
wn |
wn |
|
|
|
|
|
|
|
|||||||
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
M |
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: траектория точки – парабола y = x2/4; x ³ 0; y ³ 0. |
||||||||||||||
|
|
|
При t = 1 c vM = 2 |
|
= 2,82 см/с; wM = 2 см/с2; |
||||||||||
|
|
|
2 |
||||||||||||
|
|
|
|
wn |
= |
|
|
= 1,41 см/с |
2 ; wτ |
= 1,41 см/с2 . |
|||||
|
|
|
|
|
2 |
||||||||||
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
61 |
|
|
|
|
|
|
|
|
|
|
|
|

Исследовательская часть задачи типа 2-1 может быть посвящена определению направления касательного ускорения. Это ускорение может быть направлено либо по скорости, либо в противоположную сторону.
Для определения направления wR τ надо проверить закон изменения модуля скорости v = 
 x&2 + y&2 в зависимости от времени. Если скорость в процессе дви-
x&2 + y&2 в зависимости от времени. Если скорость в процессе дви-
жения по модулю возрастает, то касательное ускорение надо направить по направлению вектора скорости. В противном случае – наоборот.
Пример 7 (задача 3-2). Определить скорость и ускорение точки А, угловую скорость w, угловое ускорение ε колеса (рис. 4.7), если R = 1 м; r = 0,5 м; v0 = 1 м/с; w0 = 2 м/с2; φ = 240°.
а)
у |
|
ϕ |
ω |
|
|
|
|
||
|
|
|
|
|
|
|
r |
|
|
|
r |
|
|
|
|
|
V |
||
|
|
|
0 |
|
|
0 |
|
R |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
A |
VA |
|
|
|
|
|
|
|
|
|
P |
|
б) |
|
|
ε |
|
|
|
у |
|
|
|
|
||
|
|
|
W |
|
||
|
|
W |
|
0 |
||
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
δ |
W |
0 |
|
|
ос |
|
|
|
|
||
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
А0 |
|
|
|
|
|
|
|
|
A |
x |
Wвр |
|
А0 |
|
P
x
Рис. 4.7. Схемы скоростей (a) и ускорений (б) катящегося колеса
Решение. Колесо при качении по неподвижному рельсу совершает плоское движение, его мгновенный центр скоростей Р совпадает с точкой касания колеса с неподвижным рельсом.
Определим угловую скорость колеса как отношение скорости полюса v0 к расстоянию от полюса до мгновенного центра скоростей:
w = v0 = v0 = 1 =1,0 рад/с2.
OP R 1
Определим угловое ускорение колеса как производную от угловой скорости по времени:
|
dw |
|
d v |
0 |
|
1 |
|
dv |
|
w |
|
2 |
= 2,0 рад/с2 . |
||||
e = |
|
|
= |
|
|
|
= |
|
|
0 |
= |
0 |
; |
e = |
|
||
dt |
|
|
|
R |
dt |
|
1 |
||||||||||
|
|
dt R |
|
|
R |
|
|
||||||||||
Вращение вокруг полюса О ускоренное и направлено по часовой стрелке, |
|||||||||||||||||
|
R |
|
|
|
|
|
|
R |
|
|
|
|
|
|
|||
т. к. скорость н0 |
и ускорение w0 имеют одинаковое направление. Скорость точ- |
||||||||||||||||
ки А найдем как вращательную относительно мгновенного центра скоростей:
vA = wAP; AP = 
 R2 + r 2 - 2Rr cos g =
R2 + r 2 - 2Rr cos g = 
 1,02 + 0,52 - 2 ×1× 0,5cos30O = 0,39 м,
1,02 + 0,52 - 2 ×1× 0,5cos30O = 0,39 м,
62

где g = ÐAOP = 30º = 270º – j; vA = wAP = 1 · 0,39 = 0,39 м/с.
Вектор скорости vA направлен перпендикулярно прямой АР в сторону угловой скорости w вращения по часовой стрелке. Вектор ускорения точки А равен
R |
|
R |
R oc |
R |
вр |
. |
(7.1) |
|
w |
A |
= w |
+ w |
AO |
+ w |
АО |
||
|
0 |
|
|
|
|
|||
Строим при точке А составляющие ее ускорения: а) ускорение полюса w0 :
w0 = 2 м/с2 (дано в условии задачи);
б осестремительное ускорение R oc направлено по АО от точки А к полю
) wAO -
су О:
wocAO = w2r =1× 0,5 = 0,5 м/с2 ;
в) вращательное ускорение |
R |
вр |
направлено перпендикулярно радиусу ОА |
w |
АО |
||
|
|
|
|
в сторону углового ускорения ε: |
|
|
|
R вр = e = × = м с2 wАО r 2 0,5 1 / .
Для определения модуля ускорения точки А применим метод проекций: свяжем с колесом систему координатных осей и спроектируем уравнение (7.1) на эти оси:
|
|
|
|
w |
AX |
= w |
|
+ woc |
+ wвр |
; |
||
|
|
|
|
|
|
OX |
|
AOX |
AOX |
|
||
w |
AX |
= w |
+ woc |
sin 30O |
- wвр |
|
cos 30O = 2 + 0,5 × 0,5 +1× 0,87 = 1,38 м/с2 ; |
|||||
|
O |
AO |
|
|
AO |
|
|
|
|
|
|
|
|
|
wAY = wocAO cos 30O + wврAO |
|
sin 30O |
= 0,5 × 0,87 +1× 0,5 = 0,94 м/с2 . |
|||||||
Модуль полного ускорения:
wA = wAX2 |
+ wAY2 = 1,382 + 0,942 =1,67 м/с2. |
|||
d = arctg |
wAX |
= arctg |
1,38 |
= arctg 0,826; d = 39O35¢. |
|
|
|||
|
wA |
1,67 |
|
|
Ответы: w = 1,0 рад/с; e = 2,0 рад/c2 ; vA = 0,39 м/с; wA = 1,67 м/с2.
Самостоятельно провести теоретическое исследование без проведения числовых расчетов по методике определения скорости и ускорения точки А, если
R R
скорость v0 и ускорение w0 направлены в разные стороны.
63

Пример 8 (задача 3-3). Для механизма, изображенного на рис. 4.8, найти мгновенный центр скоростей шатуна АВ, угловую скорость ωAB и угловое ускорение εАВ шатуна АВ, скорость и ускорение ползуна В, если АВ = l = 100 см;
а = 30 см; ОА = r = 30 см; ωOA = 5 рад/с.
|
|
|
|
а) |
|
VA |
б) |
|
ωАО |
A |
ωАB P |
|
О |
||
|
|
АB |
a |
C |
α |
|
О |
|
|
В |
||
|
|
|
|
|
|
|
VВ |
|
|
в)
x
О
WА
A 




 εАB
εАB
 α
α 



W B
|
|
у |
|
|
|
|
ос |
|
|
W |
|
|
ВA |
|
|
|
В |
|
|
|
W |
|
|
А |
|
|
|
|
вр |
|
|
W |
|
|
ВA |
z
О
О |
|
A |
|
|
|
|
|
ос |
|
вр |
W |
|
||
W |
|
|
||
|
|
|
||
ВA |
ВA |
|
||
|
|
|
||
|
|
|
|
|
|
|
|
W |
|
|
|
W |
|
|
|
|
|
A |
|
|
|
В |
|
|



 В z
В z
Рис. 4.8. Схемы скоростей (а) и ускорений (б) и кривошипно-шатунного механизма (в)
Решение. Механизм, изображенный на рис. 4.8, состоит из кривошипа ОА, вращающегося вокруг оси О с постоянной угловой скоростью ωОА, ползуна В, поступательно движущегося в направляющих В – С, и шатуна АВ, который совершает плоское движение. Определим линейную скорость пальца кривошипа А:
vA = ωOA OA = 5 · 30 = 150 см/с.
Вектор линейной скорости точки А направлен перпендикулярно ОА в сторону угловой скорости ωОА.
Для определения положения мгновенного центра скоростей (МЦС) шатуна АВ восстановим перпендикуляры к скоростям двух точек А и В шатуна АВ; точка их пересечения РАВ – МЦС. Угловая скорость шатуна ωАВ равна отношению скорости точки А к расстоянию от этой точки до МЦС (РАВ):
ωAB |
= |
vA |
; sin α = |
a |
= |
30 |
= 0,3; |
α = 17 |
O ′ |
АPAB = l cosα = 95 см. |
||
|
|
|
|
30 ; |
||||||||
APAB |
l |
100 |
||||||||||
|
|
|
|
|
|
|
|
|||||
где cosα = 0,95;
64
wAB |
= |
vA |
= |
150 |
=1,58 рад/с. |
APAB |
|
||||
|
|
95 |
|
||
Скорость точки В определяем как вращательную вокруг мгновенного центра скоростей:
vB = wAB BPAB = wAB a = 1,58 · 30 = 47,4 см/с.
R
Вектор vB направлен вдоль направляющей ползуна В.
Определим ускорение точки В (рис. 4.8б, 4.8в). Ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения точки при вращении ее вокруг полюса. Приняв за полюс точку А, напишем выражение для ускорения точки В шатуна:
R |
R |
|
R |
R |
(8.1) |
w |
= w |
A |
+ woc |
+ wвр . |
|
B |
|
BA |
BA |
|
Вычислим и построим в точке В все составляющие ее ускорения согласно уравнению (8.1), свяжем с ней систему координатных осей хВу и запишем уравнение (8.1) в проекциях на эти оси. Ускорение полюса А направлено от А к точке О и равно
wA = wОА2 OA = 52 ×30 = 750 см/с.
Осестремительное ускорение точки В направлено по АВ от точки В к полюсу А и равно
|
|
|
wос |
= w2 |
AB = 1,582 ×100 = 250 см/с2 . |
|
|||||||||||||||
|
|
|
BA |
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вращательное ускорение точки В ( wвр |
|
) вокруг полюса направлено всегда |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
BA |
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ АВ. |
|
перпендикулярно к прямой, соединяющей точку В с полюсом, т. е. wвр |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BA |
|
Абсолютное ускорение точки В направлено вдоль направляющей. Проек- |
|||||||||||||||||||||
ция на ось Вх равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
w |
|
= w |
Aх |
+ woc |
|
+ wвр |
|
; |
|
|
|||||||
|
|
|
|
Bх |
|
|
|
|
BAх |
|
BAх |
|
|
|
|||||||
w cos a = w |
A |
cos a + woc |
w |
= |
wA cosa + wBAoc |
= |
750 × cosa + 250 |
=1013 см/с2. |
|||||||||||||
|
|
||||||||||||||||||||
B |
|
BA |
B |
|
|
|
|
|
|
|
cosa |
|
|
|
|
cos a |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Проекция на ось Ву равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
w |
= w |
Aу |
+ woc |
|
+ wвр |
; |
|
|
|
||||||||
|
|
|
|
Bу |
|
|
|
|
|
BAу |
|
BAу |
|
|
|
|
|||||
|
|
|
|
- w ×sin a = -w |
A |
sin a - wвр ; |
|
||||||||||||||
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
BA |
|
||
|
wвр |
= sin a(w - w |
A |
) = sin18O (1013 - 750) = 81,3 см/с2. |
|
||||||||||||||||
|
|
BA |
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65

Угловое ускорение шатуна АВ
eАВ = |
wвр |
|
BA |
||
АВ |
||
|
=81,3 = 0,813 рад/с2.
100
Ответ: wАВ = 1,58 рад/с; eАВ = 0,813 рад/с2; vB = 47,4 см/с; vM = 66,4 м/с; wB = 1013 см/с2.
Провести самостоятельное исследование по определению направления ус-
корения |
R |
и |
R |
, пользуясь только правилами векторной алгебры. |
w |
wвр |
|||
|
B |
|
BA |
|
Пример 9 (задача 3-4). Пластинка
(рис. 4.9), имеющая форму половины круга радиусом R = 20 см, вращается вокруг вертикальной оси АВ по закону j = (6t – 2 t2) (положительное направление отсчета угла j показано круговой стрелкой). По контуру пластинки движется точка М по закону
|
(3t - t2 ). |
S = AM = pR |
|
3 |
|
(φ – рад; S – см; t – |
с). |
Найти абсолютную скорость и аб- |
|
солютное ускорение |
точки в момент |
t = 1 с. |
|
Решение.
1. Определим положение точки М в момент t = 1 с. Имеем:
S = πR (3 -1) = |
2 |
pR. |
|
|
|||
3 |
3 |
|
|
Тогда при t = 1 с угол |
|||
ÐАСМ = S/R = 2p/3 = 120º; |
|||
ÐDCM = 30º; |
DC ^ AB. |
||
|
|
|
R |
2. Найдем абсолютную скорость va |
|||
точки М. По теореме сложения скоростей
R = R + R
va vr ve. (9.1)
Рис. 4.9. Схемы скоростей и ускорений точки М в сложном движении
66

Алгебраическая величина относительной скорости
|
|
|
~ |
|
|
πR |
(3 - 2t ). |
|
|
|
vr = S = |
|
|||
|
|
|
|
|
& |
3 |
|
|
|
|
|
|
|
|
|
В момент t = 1 с |
|
|
πR |
|
|
||
|
|
|
~ |
= |
= 21 см/с = vr . |
||
|
|
|
vr |
3 |
|||
|
|
|
|
|
|
|
|
Так как |
~ |
> 0, |
то относительная скорость направлена по касательной к |
||||
vr |
|||||||
траектории точки в сторону отсчета положительных S (рис. 4.9). Алгебраическая величина угловой скорости пластинки
ω~ = ϕ& = 6 − 4t.
В момент t = 1 с
ω~ = 6 − 4 = 2 рад/с = ω.
Так как ω~ > 0, то пластинка вращается в сторону положительного отсчета
угла j (рис. 4.9).
Модуль переносной скорости точки
vе |
= wMK = wR cos30O = 2 × 20 × |
3 |
= 34,6 см/с. |
|
|||
|
2 |
|
|
Переносная скорость направлена перпендикулярно МК и АВ в сторону |
|||
R |
R |
||
вращения. Так как vr ve , то
vа = 
 vr2 + ve2 = 40,4 см/с.
vr2 + ve2 = 40,4 см/с.
3. Найдем абсолютное ускорение точки по теореме сложения ускорений (теорема Кориолиса):
R |
R |
R |
R |
(9.2) |
wа |
= wr |
+ we |
+ wcor . |
Так как в относительном движении точка М движется по криволинейной траектории, то
w = wτ + wn. |
||
R |
R |
R |
r |
r |
r |
Алгебраическая величина относительного касательного ускорения
~τ |
|
~ |
|
πR |
|
2 |
|
= |
dvr |
= - |
2 = -42 см/с |
. |
|||
wr |
|
|
|
||||
dt |
3 |
|
|||||
|
|
|
|
|
|
Модуль касательного ускорения
wrτ = 42 см/с2.
67

Так как |
~τ |
< 0, то вектор |
R τ |
направится по касательной к траектории в |
|||
wr |
wr |
||||||
сторону отсчета отрицательных S (рис. 4.9). |
|||||||
Модуль нормального относительного ускорения |
|||||||
|
|
wn = |
vr2 |
= |
vr2 |
= 22 см/с2. |
|
|
|
r |
R |
||||
|
|
r |
|
|
|
||
|
|
|
|
|
|
|
|
Вектор |
R |
R |
от точки М к точке С. |
||||
wn направлен v |
|||||||
|
r |
r |
|
|
|
|
|
Переносное ускорение точки (ускорение движения точки вместе с пла- |
|||||||
стинкой) |
|
|
|
|
|
|
|
|
|
|
R |
R |
R |
||
|
|
|
w |
= wос + wвр. |
|||
|
|
|
|
e |
|
e |
e |
Модуль переносного осестремительного ускорения |
|||||||
|
|
woc |
= w2MK = 69,2 см/с2. |
||||
|
|
e |
|
|
|
|
|
Вектор |
R |
направлен по МК к оси вращения (МК ^ АВ). |
|||||
woc |
|||||||
|
e |
|
|
|
|
|
|
Алгебраическая величина углового ускорения пластинки
~e = dω = -4 рад/с2. dt
Модуль углового ускорения
e = ~e = 4 рад/с2.
Так как знаки ω~ и ~ε в момент t = 1 с различны, то вращение пластинки в
этот момент замедленное. Круговую стрелку ε направим противоположно круговой стрелке ω (рис. 4.9).
Модуль переносного вращательного ускорения
|
|
wвр = eМK = 4 × 20 × |
3 |
= 69,2 см/с2 . |
|
||
|
|
|
|
||||
|
|
е |
2 |
|
|
|
|
|
|
|
|
|
|
||
Вектор |
R |
направлен противоположно |
R |
с за- |
|||
wвр |
v , т. к. вращение при t = 1 |
||||||
|
е |
|
|
|
e |
|
|
медленное. |
|
|
R |
|
|
||
Определим кориолисово ускорение |
точки М. Воспользуемся прави- |
||||||
wcor |
|||||||
|
|
|
R |
на плоскость П, перпендикуляр- |
|||
лом Н. Е. Жуковского. Найдем проекцию vr |
|||||||
ную оси вращения. Имеем (рис. 4.9):
vrn = vr cos60º = 10,5 см/с.
Модуль кориолисова ускорения
wcor = 2wvrn = 2 · 2 · 10,5 = 42см/с2.
68

Направление вектора получим, если повернем vrn в указанной плоскости в сторону вращения (в сторону стрелки ω) (рис. 4.9).
Направление вектора w |
совпало с направлением вектора |
R |
Далее |
||||
wвр. |
|||||||
cor |
|
|
|
|
|
е |
|
имеем: |
|
|
|
|
|
|
|
w = wτ + wn + wвр + wос + w . |
|
(9.3) |
|||||
R |
R |
R |
R |
R |
R |
|
|
a |
r |
r |
е |
е |
cor |
|
|
Построим взаимно перпендикулярные оси Mxyz (рис. 4.9) и найдем на основании формулы (9.3) проекции абсолютного ускорения на эти оси. Находим
wax = wrτ cos 60O − wrn cos 30O − weoc = 67,2 см/с2 ; way = −weвр − wcor = 111 см/с2 ;
waz = −wrτ cos30O − wrn cos 60O = 47,3 см/с2.
Модуль абсолютного ускорения точки t = 1 с
wa = 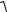
 wax2 + way2 + waz2 = 134 см/с2.
wax2 + way2 + waz2 = 134 см/с2.
Ответ: va = 40,4 см/с; wa = 134 см/с2.
В качестве теоретического исследования по этой задаче можно рекомендовать другой закон изменения угла ϕ = 6t + 2t2. Исследование провести без выполнения расчетов.
Указание. Новый закон изменения угла φ приведет к тому, что вращение по круговой
стрелке ω будет ускоренным, это только изменит направление ускорения |
R вр |
на противопо- |
wе |
||
ложное. |
|
|
4.3. Динамика
Ниже подробно рассмотрен процесс решения задач типа 4-1, 4-2, 5-1, 5-2,
5-3, 5-4, 6-1, 6-2, 6-3.
Задачи типа 5-2, 5-3, 5-4 будут предложены на экзамене.
Пример 10 (задача 4-1). На наклонном участке АВ трубы (рис. 4.10) на груз массой m действуют сила тяжести Р и сила сопротивления R; расстояние от точки А до точки В равно l. На горизонтальном участке ВС на груз действуют сила трения Fтр, переменная сила Fx = F(t) и реакция N2.
Дано: m = 2кг; R = μv2, где μ = 0,2 кг/м; АВ = l = 4 м; Fx = 2(1 + t)H; f = 0,2; α = 60º; v0 = 20 м/с; β = 0, т. к. участок ВС горизонтальный.
69

Решение.
1. Рассмотрим движение груза на участке АВ, вдоль которого направим ось х1. Изобразим промежуточное текущее положение груза
и приложенные к нему силы = R
P mg, R, N.
Составим дифференциальное уравнение движения груза:
m&x&1 = -mg sin a - R = -mg sin a - mv2.
Примем во внимание, что x&1 = v, тогда
&x&1 = dx&1 = dv . dt dt
y
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N2 |
C |
|
|
|
|
Fтр |
|
x |
|
N1 |
|
B |
|
|
|
|
|
|
|
Fx |
|
|
|
|
|
|
P |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P=mg |
|
|
|
||
V0 |
α |
|
|
|
|
|
A |
|
|
|
|
|
|
Рис. 4.10. Расчетная схема
Дифференциальное уравнение преобразуется к виду |
|
|||||||||||||||||||||
|
|
|
dv |
|
m mg sin a |
|
2 |
|
|
|||||||||||||
|
|
|
|
|
= - |
|
|
|
|
|
|
|
|
|
|
|
|
+ v |
|
. |
(10.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|||||||
|
|
|
dt |
|
m |
|
|
|
|
|
|
|
|
|||||||||
Введем обозначение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a2 = |
mg sin a |
= 85 м2 |
/с2 . |
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Умножим обе части равенства (10.1) на дифференциал dx1 и затем выпол- |
||||||||||||||||||||||
ним разделение переменных с переходом на интегралы. |
|
|||||||||||||||||||||
Находим, что dv × v = - |
m |
(a2 + v2 )dx , |
где учтено, что |
|
||||||||||||||||||
|
|
|||||||||||||||||||||
|
m |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
v = |
dx1 |
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
v × dv |
|
= - |
m |
|
dx . |
|
|
|
||||||||||
|
|
∫ a2 + v2 |
m ∫ |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Интегралы табличные после интегрирования получим |
|
|||||||||||||||||||||
|
ln(a2 + v2 )= - |
2μ |
x + C , |
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
1 |
1 |
|
|
|
||||
где C1 – произвольная постоянная.
По начальным условиям x1 = 0; v = v0 при t = 0 найдем
C1 = ln (a2 + v02 ).
70
