34. Общие индексы затрат на производство и себестоимости единицы продукции. Экономическая сущность числителя и знаменателя в общих индексах.

Общий индекс себестоимости по методу Пааше:

—затраты на выпуск разноименной продукции в отчетном периоде;

—затраты на выпуск разноименной продукции отчетного периода по себестоимости базисного периода;

Общий индекс себестоимости по методу Ласпейреса:

—затраты на выпуск одноименной продукции базисного периода по себестоимости отчетного периода;

—затраты на выпуск разноименной продукции базисного периода по себестоимости отчетного периода.

—затраты на выпуск одноименной продукции в базисном периоде;

—затраты на выпуск разноименной продукции в базисном периоде.

Общий индекс затрат на производство продукции:

35. Взаимосвязь индексов (на примере количественных и качественных показателей).

Между общими индексами количественных, качественных и стоимостных показателей существует такая же связь, как и между аналогичными индивидуальными индексами:

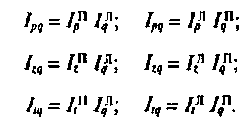
Верхний индекс «Л» указывает на метод Ласпейреса, «П» — Пааше.

Для общих индексов можно выполнить проверку расчетов и через абсолютные стоимостные показатели. Изменение товарооборота в фактических ценах, исчисленное по, равно сумме изменений товарооборота, исчисленных по:

Общий индекс агрегирует изменение индексируемого показателя по разным единицам, отсюда возникает возможность проверки расчетов вторым способом. Изменение товарооборота в фактических ценах по всем единицам равно сумме соответствующих изменений по отдельным единицам.

Связь общих индексов, как и индивидуальных, используется для приближенного расчета любого третьего индекса по известным двум.

36. Среднеарифметический индекс, тождественный агрегатному.

Агрегатные индексы цен, физического объема товарооборота и другие могут быть рассчитаны, если известны индексируемые величины и веса, т. е. p и q. Допустим, что имеется произведение pq и индивидуальные индексы. Возникает проблема построения

средних индексов, идентичных агрегатным, путем осреднения индивидуальных индексов. Эта задача решается преобразованием агрегатного индекса в среднеарифметический и среднегармонический индексы.

Преобразование агрегатного индекса в среднеарифметический можно рассмотреть на примере агрегатного индекса физического объема товарооборота. В данном случае индивидуальные индексы должны быть взвешены на базисные соизмерители.

Из индивидуального индекса физического объема товарооборота iq = q₁ / q₀ следует, что q₁ = = i_q / q₀.

Если заменить q1 в числителе агрегатного индекса физического объема товарооборота Iq = Σq₁p₀ / Σq₀p₀ на i_qq₀, то получим Iq == Σi_qq₀p₀ / Σq₀p₀. Это среднеарифметический индекс физического объема товарооборота.