17. Шкалы интервалов и интервальные переменные применяются для отображения величины различия между свойствами объектов. Например, температура, измеренная в градусах Фаренгейта или Цельсия, образует интервальную шкалу. Вы можете не только сказать, что температура 40 градусов выше, чем температура 30 градусов, но и что увеличение температуры с 20 до 40 градусов вдвое больше увеличения температуры от 30 до 40 градусов. Шкала может иметь произвольные точки отсчета и масштаб. Например, шкала Цельсия имеет условный нуль отсчёта (точку замерзания воды) и условную же единицу измерения (одну сотую расстояния от точки замерзания до точки кипения).

Шкалы интервалов инвариантны относительно линейных преобразований типа .

- Шкалы отношений и относительные переменные используются, например, для измерения массы, длины, веса. В этой шкале числа отражают отношения свойств объектов, т.е. во сколько раз свойство одного объекта превосходит свойство другого. В шкалах отношений измеряется большинство скалярных физических величин: длина, масса, энергия, температура по Кельвину и т. д. Относительные переменные очень похожи на интервальные переменные. В дополнение ко всем свойствам переменных, измеренных в интервальной шкале, их характерной чертой является наличие определенной точки абсолютного нуля. Таким образом, для этих переменных являются обоснованными предложения типа: x в два раза больше, чем у. Типичными примерами шкал отношений являются измерения температур, времени или пространства. Например, температура по Кельвину образует шкалу отношений, и вы можете не только утверждать, что температура 200 градусов выше, чем 100 градусов, но и что она вдвое выше. Интервальные шкалы (например, шкала Цельсия) не обладают данным свойством шкалы отношения.

Заметим, что в большинстве статистических процедур не делается различия между свойствами интервальных шкал и шкал отношения.

Шкалы отношений инвариантны относительно линейных преобразований, где .

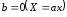- Шкалы разностей и разностные переменные используются для измерения свойств объектов при необходимости выражения, на сколько один объект превосходит другой (по одному или нескольким признакам), является частным случаем шкалы интервалов при выборе единицы масштаба. Эти шкалы используются для измерения «фаз» различных периодических процессов (например, фаз Луны или фаз переменного тока); для них существует естественная единица измерения (один полный цикл), но нет безусловного начала отсчёта.

Шкалы разностей инвариантны относительно линейных преобразований, где

.

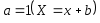18. Иерархические структуры.Слои

Второй вид многоуровневой
структуризации предложен М. Месаровичем для организации процессов
принятия решений. Для уменьшения неопределенности ситуации выделяются уровни сложности принимаемого решения - слои, т. е. определяется совокупность последовательно решаемых проблем. При этом выделение проблем осуществляется таким образом, чтобы решение вышележащей определяло бы ограничения (допустимую степень упрощения) при моделировании
на нижележащем уровне, т. е. снижало бы неопределенность нижележащей
проблемы, но без утраты замысла решения общей проблемы. Многослойную иерархию можно проиллюстрировать :


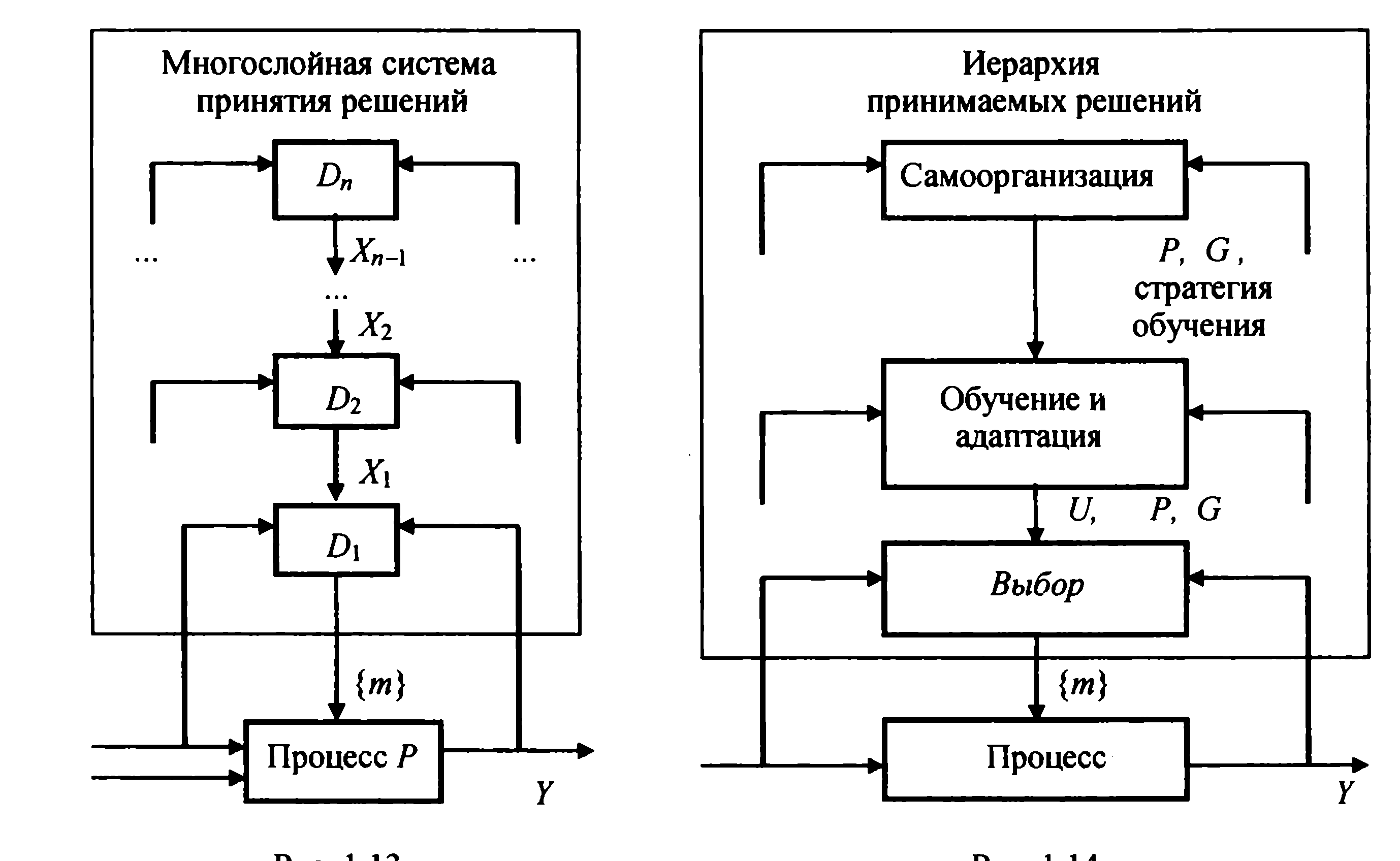
каждый слой представляет собой блок Diy принимающий решения и вырабатывающий ограничения Xj для нижележащего (n - 1)-го блока. В качестве примера рассмотрим многослойную иерархию принятия
решения по управлению каким-либо процессом. В ней можно выделить
 три основных аспекта проблемы принятия решения в условиях неопределенности, приведенные на рисунке. Нижний слой, самый «близкий» к управляемому процессу, слой выбора. Задача этого слоя - выбор способа действий m. Принимающий
решения элемент (блок) получает данные (информацию) об управляемом
процессе и, применяя алгоритм, полученный на верхних слоях, находит нужный способ действия, т.е. последовательность управляющих воздействий на управляемый процесс. Алгоритм может быть определен непосредственно как функциональное отображение Д, дающее решение для
любого набора начальных данных. Для примера предположим, что заданы выходная функция Р и функция
оценки G, а выбор действий {m} основан на применении оценки G к Р. Используя теоретико-множественные представления, выходную функцию можно определить как отображение Р: М х U —> У, где М - множество альтернативных действий; У - множество возможных результатов на выходе (или «выходов»); U - множество неопределенностей, адекватно отражающее отсутствие знаний о зависимости между действием т и выходом У. Аналогично функция оценки G есть отображение G: М х К—> V, где V -
множество величин, которые могут бьггь связаны с характеристиками качества
работы системы. Если множество U состоит из единственного элемента или
является пустым, т. е. относительно результата на выходе для данного действия т нет неопределенности, выбор может основываться на оптимизации: найти такое т' в М, чтобы величина v' = G(m’, Р(m')) была меньше, чем
v = G(m, Р(т)) для любого другого действия те М. Если U- более богатое множество, приходится предлагать некоторые другие процедуры для выбора способа решения. Возможно при этом придется ввести и некоторые другие отображения, помимо Р и G. Но в общем случае для того, чтобы определить задачу выбора
на первом слое, необходимо уточнить множество неопределенностей U, требуемые отношения Р, G и т. д. Это осуществляется на верхних слоях. Вышележащий по отношению к рассматриваемому слою - слой обучениями адаптации. Задача этого слоя - конкретизировать множество неопределенностей U, с которым имеет дело слой выбора. Множество неопределенностей U рассматривается здесь как множество, включающее в себя все
незнание о поведении системы и отражающее все гипотезы о возможных источниках и типах таких неопределенностей. U может быть получено с помощью наблюдений и внешних источников информации. Назначение рассматриваемого слоя - сузить множество неопределенностей U и таким образом упростить модель слоя выбора. В случае стационарности системы и среды множество U может быть предельно сужено вплоть до одного элемента,
что соответствует идеальному обучению. Однако в общем случае U может
включать не только существующие, но и предполагаемые системой принятия решения неопределенности, и в случае необходимости U может быть
полностью изменено, расширено, в том числе за счет изменения ранее принятой базисной гипотезы. Третий, в данном случае верхний, - слой самоорганизации. На этом слое
выбираются структура, функции и стратегии, используемые на нижележащих слоях, таким образом, чтобы по возможности приблизиться к отображению цели, которая обычно задается в форме вербального описания. Если
цель не достигается, могут быть изменены функции Р и G на первом слое
или стратегия обучения на втором. Многослойные системы принятия решений полезно формировать для
решения задач планирования и управления промышленными предприятиями, отраслями, народным хозяйством в целом. При постановке и
решении таких проблем нельзя раз и навсегда определить цели, выбрать
конкретные действия: экономические и технологические условия производства непрерывно изменяются. Все это можно отразить в многослойной модели принятия решений. Примером приложения идеи выделения слоев могут служить многоуровневые экономико-математические модели планирования и управления отраслями, народным хозяйством, разрабатываемые в нашей стране в 70-80-х гг., а
позднее - и промышленными предприятиями.