
- •Лекция 1 Введение.
- •Свойства жидкостей.
- •Лекция 2 Гидростатика
- •Гидростатическое давление и его свойства.
- •Дифференциальные уравнения равновесия жидкости (уравнения л. Эйлера)
- •Уравнение гидростатики
- •Закон Паскаля
- •Пьезометрическая высота
- •Удельная потенциальная энергия
- •Лекция 3 Приборы для измерения давления
- •Силы давления жидкости на поверхности
- •Вектор силы давления жидкости на криволинейную стенку
- •Определение толщины стенок труб, воспринимающих внутреннее давление жидкости и силы в колене трубы.
- •Закон Архимеда и плавание тел
- •Остойчивость тел
- •Лекция 4. Гидродинамика.
- •Основные гидродинамические понятия.
- •Дифференциальные уравнения движения идеальной жидкости (уравнения Эйлера)
- •Дифференциальные уравнения неразрывности движущейся жидкости
- •Уравнение неразрывности
- •Лекция 5. Уравнение установившегося движения элементарной струйки идеальной жидкости (уравнение д.Бернулли)
- •Механическая энергия потока жидкости
- •4.4. Уравнение Даниила Бернулли для потока реальной жидкости.
- •Примеры практического применения уравнения д. Бернулли Трубы Вентури
- •Гидродинамическая трубка Пито.
- •4.5.3. Гидродинамическая трубка Пито - Прандтля.
- •4.5.4. Водоструйный насос (эжектор).
- •Карбюратор.
- •Лекция 6. Режимы движения вязкой жидкости. Число Рейнольдса. Скорость и расход жидкости при ламинарном режиме.
- •Режимы движения жидкости.
- •Силы трения и закон распределения скоростей при ламинарном и турбулентном режимах движения жидкости.
- •Турбулентное движение.
- •Лекция 7 Классификация потерь напора
- •Местные сопротивления трубопроводов
- •Лекция 8. Основы расчета трубопроводов Типы трубопроводов и их классификация
- •Методика расчета простого трубопровода.
- •Расчет гидравлически коротких трубопроводов
- •Расчет сифонного трубопровода.
- •Лекция 9. Гидравлический удар в трубопроводах
- •Истечение жидкости через отверстия и насадки (общие сведения)
- •Обозначим
- •Истечение жидкости из насадков
- •Цилиндрический внутренний насадок
- •Истечение жидкости через большие отверстия.
- •Истечение жидкости при переменном напоре
- •Гидравлические струи
- •Расчет турбин
- •Лекция 10. Равномерное движение в открытых руслах
- •Скорость при равномерном движении выражается формулой
- •Водосливы. Классификация водосливов
- •Гидравлический расчет отверстий малых мостов и водопропускных дорожных сооружений
- •Гидравлический расчет открытых русел
- •Лекция 11. Основы теории гидравлического моделирования
- •Закон Фруда
- •Закон Рейнольдса
Лекция 8. Основы расчета трубопроводов Типы трубопроводов и их классификация
В зависимости от величины местных потерь все трубопроводы делятся на гидравлически длинные и гидравлически короткие.
Трубопроводы, у которых основными являются потери по длине, а мелкими потерями можно пренебречь, называются гидравлически длинными трубопроводами (водопроводами).
Трубопроводы, у которых преобладают местные потери - короткими.
Простой трубопровод - из труб одного или двух диаметров и не имеет ответвлений.
Сложный трубопровод имеет магистраль с разветвлениями: разветвленные или тупиковые, замкнутые или кольцевые.
Расчет длинных трубопроводов:
- определить
![]() ,
при известных
,
при известных![]() ,
,![]() и
и
![]() ;
;
- определить
![]() при известных
при известных![]() ,
,
![]() иl;
иl;
- определить
![]() ,
при заданных
,
при заданных![]() и
и![]() .
.
Используется уравнение Бернулли:
![]() (110)
(110)
и уравнение постоянства расхода:
![]() (111)
(111)
Уравнение Бернулли приводятся к двум видам:
![]() (112)
(112)
![]() (113)
(113)
Выражая расход через расходную характеристику К и гидравлический уклон I получим:
![]() (114)
(114)
![]() ,
(115)
,
(115)
где С - коэффициент потерь Шези;
R - гидравлический радиус, м.
Потери по всей длине трубопровода подсчитывается по формуле:
для квадратичной области -
![]() (116)
(116)
для Ι и ΙΙ зон -
![]() (117)
(117)
Коэффициенты
гидравлического трения
![]() необходимо определить по формулам,
приведенным выше в зависимости от числа
Рейнольдса и относительной шероховатости
или по графику
необходимо определить по формулам,
приведенным выше в зависимости от числа
Рейнольдса и относительной шероховатости
или по графику
![]() (118)
(118)
Правила выбора сечений:
сечения всегда выбираются перпендикулярно направлению движения жидкости;
сечение выбираются там, где известно максимальное число слагаемых уравнения Бернулли или там, где нужно что-то определить;
нумеровать сечения следует так, чтобы жидкость двигалась от 1 - 1 к 2 - 2.
Методика расчета простого трубопровода.
Первый случай:
Имеем
простой трубопровод с постоянным
диаметром
![]() ,
который работает под напором
,
который работает под напором
![]() .
.


Рис. 41 Схема расчета прямого трубопровода (случай первый)
Для сечений 1 - 1 и 2 - 2 напишем уравнение Бернулли:
![]() .
.
Так как
![]()
![]() ,
давление
,
давление![]() ,
тогда уравнение примет вид:
,
тогда уравнение примет вид:
![]() (119)
(119)
Так как мы имеем гидравлически длинный трубопровод, то пренебрегая местным сопротивлением, получим
![]() (120)
(120)
где
![]() и
и![]() .
.
С учетом местных потерь
![]() (121)
(121)
Второй случай:
Трубопровод состоит из последовательно соединенных труб разных диаметров.

Рис. 42 Схема расчета простого трубопровода (случай второй)
Три участка длиной
![]() ,
,
![]() ,
,
![]() с равными диаметрами труб
с равными диаметрами труб![]() ,
,
![]() ,
,
![]() .
Напор будет расходоваться на преодоление
потерь напора по длине:
.
Напор будет расходоваться на преодоление
потерь напора по длине:
![]() (122)
(122)
Потери на любом участке определим по формуле:
![]() (123)
(123)
тогда
 (144)
(144)
или
![]() (145)
(145)
Расчет гидравлически коротких трубопроводов
Первый случай:
Истечение жидкости под уровень.

Рис. 43 Схема расчета короткого трубопровода (случай первый)
Жидкость перетекает
из А в В.
Длина трубы
![]() ,
диаметр
,
диаметр![]() ,
разность уровней
,
разность уровней![]() .
Движение - установившееся.
.
Движение - установившееся.
Пренебрегая
скоростными
напорами
и
![]() ,
уравнение Бернулли имеет вид:
,
уравнение Бернулли имеет вид:
![]() (126)
(126)
Потери напора
![]() - вход в трубу, кран, два поворота, кран
и выход из трубы:
- вход в трубу, кран, два поворота, кран
и выход из трубы:
![]() (127)
(127)
![]() ;
;
![]()
![]() (128)
(128)
Обозначим
![]() - коэффициент сопротивления системы.
- коэффициент сопротивления системы.
Так как
![]() ,
,
то
![]() (129)
(129)
![]() (130)
(130)
![]() (131)
(131)
Обозначим:
![]() ,
,
тогда
![]() , (132)
, (132)
где
![]() -
коэффициент расхода системы;
-
коэффициент расхода системы;
![]() - площадь живого
сечения потока, м2.
- площадь живого
сечения потока, м2.
Второй случай:
Истечение жидкости в атмосферу.

Рис. 44 Схема расчета короткого трубопровода (случай второй)
Из уравнения Бернулли для сечений 1 - 1 и 2 - 2, получим
![]() (133)
(133)
где
![]() (134)
(134)
Подставив, имеем
![]() (135)
(135)
Обозначим
![]() ,
,
тогда
![]() (136)
(136)
и
![]() (137)
(137)
Расход жидкости:
![]() (138)
(138)
или
![]() (139)
(139)
где
![]() - коэффициент расхода системы.
- коэффициент расхода системы.
Пример. Определить
расход керосина Т-1
при температуре
![]() ,
протекающего по трубопроводу из сваренных
труб из нержавеющей стали в пункты 1
и 2 (рис. 45), если
напор Н
в резервуаре постоянный и равный 7,2
м.
Длина отдельных частей трубопровода
,
протекающего по трубопроводу из сваренных
труб из нержавеющей стали в пункты 1
и 2 (рис. 45), если
напор Н
в резервуаре постоянный и равный 7,2
м.
Длина отдельных частей трубопровода
![]() ,
диаметры:
,
диаметры:
![]() ,
,
![]() .
Местные потери напора в расчетах не
учитывать.
.
Местные потери напора в расчетах не
учитывать.

Рис. 45. Схема трубопровода с параллельными ветвями
Так как трубы 1 и 2 параллельны, то потерянные напоры в этих трубах
![]()
или
![]() (140)
(140)
По
условию задачи размеры параллельных
труб, изготовленных из одного материала,
одинаковы (![]() ,
,
![]() )
поэтому
)
поэтому
![]() и
и
![]()
Следовательно,
![]() ;
;
![]() (141)
(141)
где
![]() -
расход
в трубопроводе;
-
расход
в трубопроводе;
![]() ,
,![]() - расход в параллельных ветвях трубопровода.
- расход в параллельных ветвях трубопровода.
Уравнение Бернулли для сечений 0 - 0 и 1 - 1 (см. рис. 45)
![]()
Так
как
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
то
![]()
или
 (142)
(142)
Уравнение
(142) можно решить только графоаналитическим
способом. Задаемся разными значениями
расхода жидкости в трубопроводе и для
этих значений
![]() вычисляем
вычисляем
![]() и
и
![]() :
:
![]() ;
;
(143)
![]() .
.
По
известным величинам
![]() и
и
![]() ,
,
![]() и
и
![]() определяем
числа Рейнольдса
определяем
числа Рейнольдса
![]() и
и
![]() :
:
![]() ,
,
![]() (144)
(144)
Для
керосина Т
- 1
![]() ,
,
![]() .
.
У
сварных труб из нержавеющей стали
эквивалентная шероховатость
![]() ,
поэтому относительная эквивалентная
шероховатость труб
,
поэтому относительная эквивалентная
шероховатость труб
![]() ;
;
![]() .
.
По
известным величинам
![]() и
и
![]() ,
,
![]() и
и
![]() по графику Колбрука определяем
коэффициенты сопротивления трения
по графику Колбрука определяем
коэффициенты сопротивления трения
![]() и
и
![]() и далее по уравнению (142) устанавливаем
необходимый напор. Расчет сводим в
таблицу
5.
и далее по уравнению (142) устанавливаем
необходимый напор. Расчет сводим в
таблицу
5.
Таблица 5
-
Расчет гидравлической характеристики трубопроводов
 ,
,
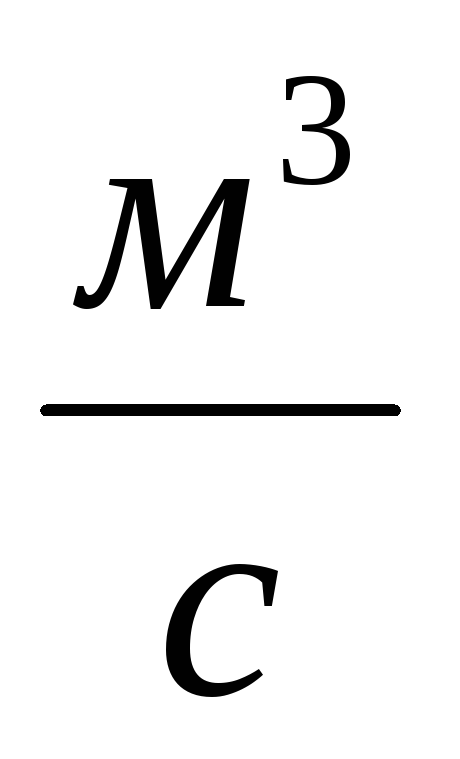
2
5
8
 ,
,

1,02
2,55
4,09

2,04
5,10
8,18

0,032
0,026
0,0245
 ,
,
0,053
0,332
0,851
 ,
,

0,312
1,54
3,83
 ,
,

0,795
1,99
3,19

1,27
3,18,
5,10

0,032
0,0285
0,028
 ,
,
0,0322
0,202
0,519
 ,
,

0,23
1,33
3,34
 ,
,
0,574
3,07
7,69
