Силы трения и закон распределения скоростей при ламинарном и турбулентном режимах движения жидкости.

При ламинарном режиме движения жидкости в трубе в ней возникают силы трения и она начинает двигаться как бы цилиндрическими бесконечно тонкими слоями с различными скоростями. Скорости слоев жидкости от продольной оси трубопровода к ее стенкам уменьшаются по параболическому закону. На оси трубы они имеют максимальное значение. На поверхности стенок трубы скорость течения равна нулю. Слои жидкости, движущиеся с меньшей скоростью тормозят движение слоев, имеющих большую скорость. Цилиндрические слои жидкости, движущиеся с большей скоростью, скользят по слоям жидкости, движущимся с меньшей скоростью. На поверхностях смежных слоев жидкости благодаря наличию сцепления частиц жидкости между собой и со стенками, ограждающими поток, в процессе скольжения развивают силы трения. Силы трения, появившиеся на граничащих поверхностях между слоями жидкости, осуществляют тормозящее действие, что и приводит к возникновению разных скоростей движения отдельных частиц жидкости.

Главной причиной возникновения сил трения при движении потока следует считать разность скоростей между движущимися слоями жидкости. Чем больше разность скоростей, тем больше по величине возникающие силы трения, силы гидравлических сопротивлений.

Рассмотрим ламинарный режим движения в цилиндрической трубе (рис. 32). В модели такое движение можно представить состоящим из множества телескопически выдвинутых цилиндров толщиной . Огибающую этих цилиндров можно рассматривать как эпюру скоростей струек.

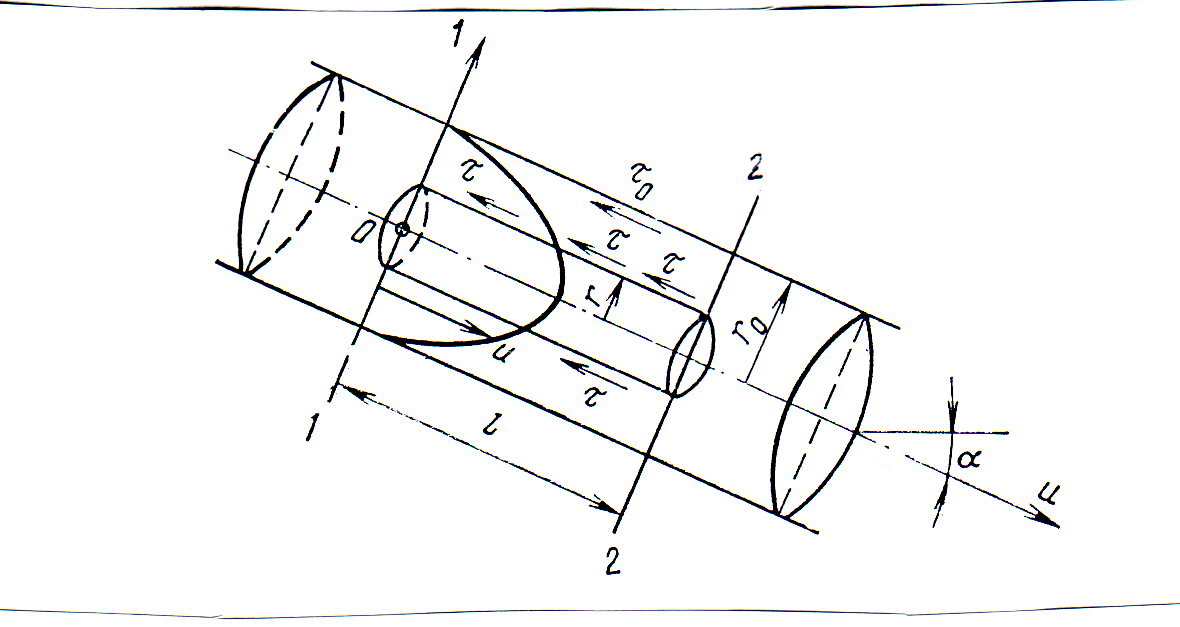
Рис. 32. Эпюра скоростей при ламинарном режиме движения

Касательное напряжение на боковой поверхности выделенного цилиндра определим в соответствии с законом Ньютона о силе сопротивления в жидкости, а именно

При направлении координатных осей и, указанном на рис. 32 – ось скоростивдоль оси трубы, ось нормали к направлению скорости – вдоль радиусаможем записать:

Знак минус потому, что здесь при имеем.

После подстановки в уравнение равномерного движения получим дифференциальное уравнение распределения скорости в таком виде:

Проинтегрировав, найдем

Определим постоянную интегрирования С по условиям на границе. В точке у стенки трубы , т.е. радиусу трубы, а скорость. Тогда

и

Следовательно, уравнение примет вид:

или окончательно

(88)

Тогда расход потока в трубе

(89)

Разделив (88) на , найдем среднюю скорость

(90)

Следовательно, средняя скорость равна половине максимальной.

Потерянный напор найдем из (90), учитывая, что :

.

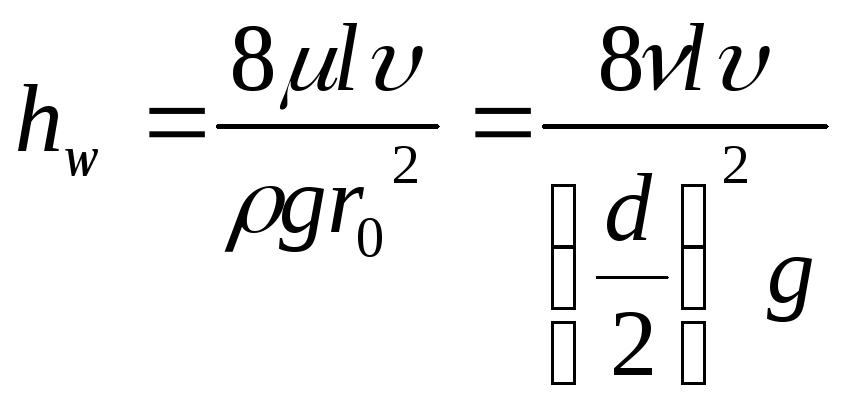Умножив и разделив правую часть на и затем преобразовав, получим:

.

Но , тогда

или, обозначив ,

. (91)

Формула (91), как известно, называется формулой Дарси-Вейсбаха. Здесь - коэффициент гидравлического сопротивления в трубах. Как видно, при ламинарном движении коэффициентявляется функцией числа Рейнольдса.