Дифференциальные уравнения движения идеальной жидкости (уравнения Эйлера)

Формально общие уравнения движения идеальной жидкости можно получить из уравнений, составленных для покоящейся жидкости, если воспользоваться принципом Д. Аламбера, согласно которому к уже действующим силам добавляются силы инерции.

Обозначим силу инерции, отнесенную к единице массы движущейся идеальной жидкости 1. Тогда проекции этой силы на координатные оси будут равны: -1; -1и -1. Знак минус в данном случае указывает на то, что единичная сила инерции имеет направление противоположное ускорению.

С учетом сказанного дифференциальные уравнения движения идеальной жидкости получает вид:

(56)

Для случая неустановившегося движения, когда полный дифференциал скорости, например, равен

,

тогда

.

С учетом аналогичных выражений, полученных для и, дифференциальные уравнения неустановившегося движения идеальной жидкости получают следующий вид:

(57)

Для установившегося движения идеальной жидкости, когда , дифференциальные уравнения движения идеальной жидкости имеют вид

(58)

Системы дифференциальных уравнений (57) и (58) называются системами дифференциальных уравнений движения идеальной жидкости, представленными в развернутом виде.

Уравнения (56) – (58) применимы как для случаев движения капельных жидкостей (когда ), так и для движения газов (когда).

Дифференциальные уравнения неразрывности движущейся жидкости

В системе из трех дифференциальных уравнений движения идеальной жидкости (56) содержится четыре неизвестных параметра движения ;;;. Для того, чтобы определить эти параметры, необходимо четвертое уравнение. Таким уравнением является дифференциальное уравнение неразрывности.

Выделим в движущейся идеальной жидкости параллелепипед (рис. 21) со сторонами ;;, представляющий собой неподвижную часть пространства, заполненного движущейся жидкостью. Будем считать, что движение жидкости происходит без образования пустот и переуплотнений, т.е. с постоянной плотностью.

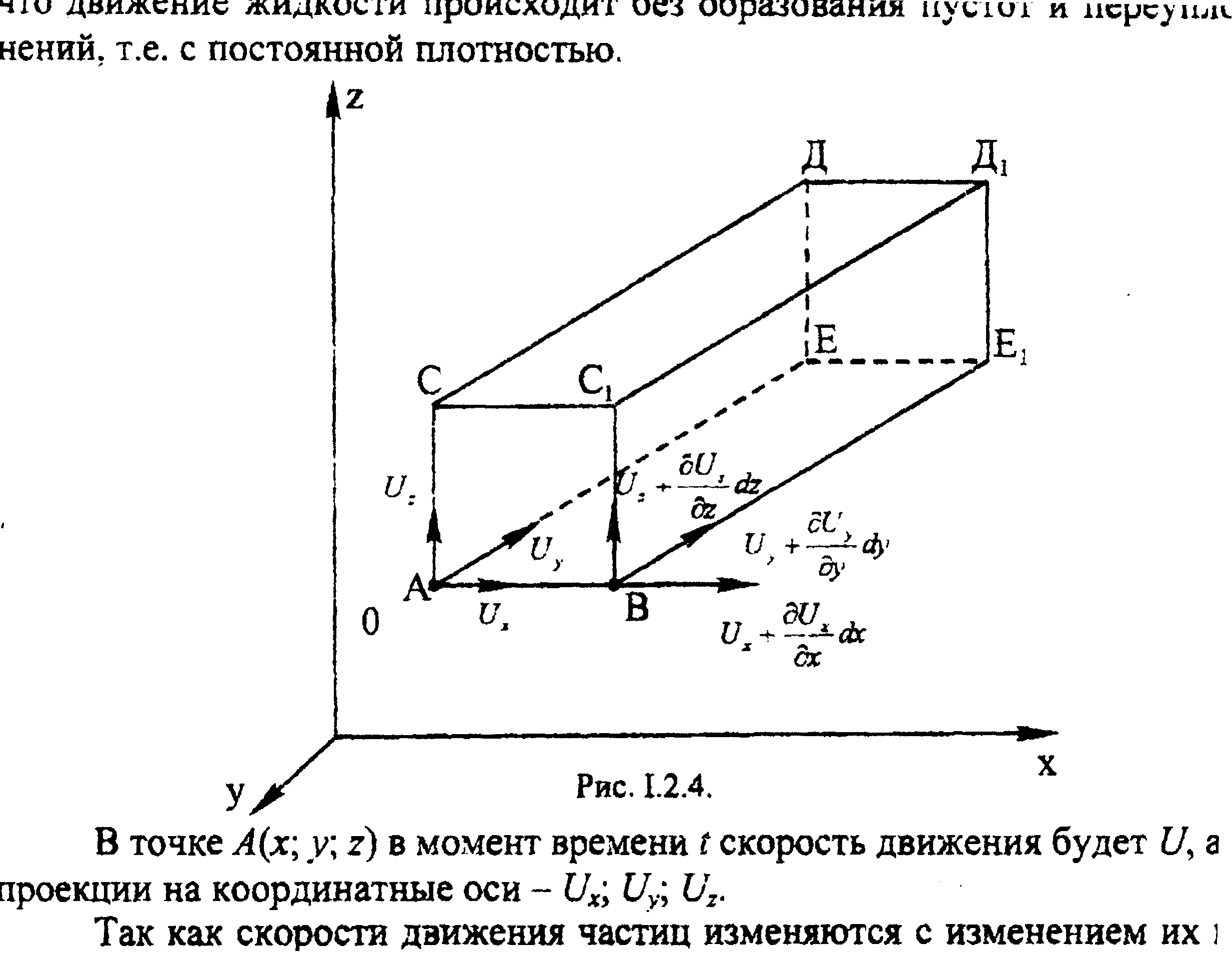
Рис. 21.

В точке А в момент временискорость движения будет, а ее проекции на координатные оси -.

Так как скорости движения частиц изменяются с изменением их положения в пространстве, то в тот же момент времени скорость в точкеВ , отстоящей от точкиА на расстоянии будет равна. Частная производная в градиенте давленияпринята потому, что при переходе частицы из точкиАв точку В меняется только координата .

Таким образом, за время через грань АСДЕ параллелепипеда будет втекать жидкость массой

а через грань ВС₁Д₁Е₁вытекать

.

Следовательно, за время изменение массы жидкости в параллелепипеде в результате движения через грани, нормальные к осибудет равно

.

Изменения массы жидкости через грани нормальные к осям исоответственно будут равны

;

.

Так как форма параллелепипеда остается неизменной, а движение жидкости происходит без образования пустот и переуплотнений, общая сумма изменений массы внутри параллелепипеда будет равна нулю, т.е.

или после сокращения:

(59)

Физический смысл уравнения (59) состоит в том, что сумма изменений проекций скоростей в направлении соответствующих координатных осей равна нулю. Это значит, что объем несжимаемой жидкости, которая втекает в параллелепипед, равна объему жидкости, вытекающему из него.