Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ухтинский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

книги бурение / Технология переработки природного газа и конденсата / 3

.pdf

Скачиваний:

Добавлен:

02.03.2016

Размер:

3.61 Mб

Скачать

☆

1 / 141 2 3 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

иЦкЦкДЕйндД икакйСзйЙй ЙДбД а дйзСЦзлДнД

3.1. ейСЦгакйЗДзаЦ икйсЦллйЗ иЦкЦкДЕйнда ЙДбД а дйзСЦзлДнД

3.1.1. оДбйЗхЦ кДЗзйЗЦлаь З езйЙйдйеийзЦзнзхп леЦльп, лйСЦкЬДфап

дйеийзЦзнх икакйСзйЙй ЙДбД, ЗйСм, еЦнДзйг, Йгадйга

и Л ‡Т˜ВЪ‡ı Ф УˆВТТУ‚ ФВ В ‡·УЪНЛ Ф Л У‰МУ„У „‡Б‡ М‡Л·УОВВ ‚‡КМУИ Л Ъ Ы‰МУИ Б‡‰‡˜ВИ ﬂ‚ОﬂВЪТﬂ ‡Т˜ВЪ Щ‡- БУ‚У„У ‡‚МУ‚ВТЛﬂ КЛ‰НУТЪ¸ – Ф‡ . и Л ˝ЪУП Ъ В·ЫВЪТﬂ УФ В- ‰ВОЛЪ¸ ТУТЪ‡‚ Щ‡Б Л Лı НУОЛ˜ВТЪ‚У. З ТПВТﬂı, ТУ‰В К‡˘Лı ‚У‰Ы, ПВЪ‡МУО, „ОЛНУОЛ, ‚УБПУКМУ ‚˚‰ВОВМЛВ ‚ЪУ УИ КЛ‰НУИ Щ‡Б˚.

ê‡‚ÌÓ‚ÂÒËÂ ÊË‰ÍÓÒÚ¸ – Ô‡

б‡ФЛ¯ВП Ы ‡‚МВМЛﬂ П‡ЪВ Л‡О¸МУ„У ·‡О‡МТ‡ ‰Оﬂ У‰- МУ„У ПУОﬂ ТПВТЛ Л Н‡К‰У„У НУПФУМВМЪ‡:

V + L = 1;			(3.1)
Vyi + Lxi = zi;			(3.2)
n	n	n
∑ yi = ∑ xi = ∑ zi = 1,			(3.3)
i=1	i=1	i=1

„‰Â V – ÏÓÎ¸Ì‡ﬂ ‰ÓÎﬂ „‡ÁÓ‚ÓÈ Ù‡Á˚; L – ÏÓÎ¸Ì‡ﬂ ‰ÓÎﬂ ÊË‰ÍÓÈ Ù‡Á˚; yi – ÏÓÎ¸Ì‡ﬂ ‰ÓÎﬂ i НУПФУМВМЪ‡ ‚ „‡БУ‚УИ Щ‡БВ; xi – ÏÓÎ¸Ì‡ﬂ ‰ÓÎﬂ i НУПФУМВМЪ‡ ‚ КЛ‰НУИ Щ‡БВ; zi – ÏÓÎ¸Ì‡ﬂ ‰ÓÎﬂ i НУПФУМВМЪ‡ ‚ ТПВТЛ.

к‡ТФ В‰ВОВМЛВ НУПФУМВМЪУ‚ ПВК‰Ы Щ‡Б‡ПЛ М‡Л·УОВВ ˜‡ТЪУ ‚˚ ‡К‡˛Ъ ˜В ВБ НУМТЪ‡МЪ˚ Щ‡БУ‚У„У ‡‚МУ‚ВТЛﬂ:

Ki = yi/xi.	(3.4)
	99

дУП·ЛМЛ Ыﬂ Ф Л‚В‰ВММ˚В Ы ‡‚МВМЛﬂ, ПУКМУ ФУОЫ˜ЛЪ¸

yi =	zi	.	(3.5)
	V +(1−V)/Ki

кВ¯‡ﬂ ˝ЪЛ Ы ‡‚МВМЛﬂ ПВЪУ‰УП ФУТОВ‰У‚‡ЪВО¸М˚ı Ф Л·ОЛКВМЛИ, ФУОЫ˜‡˛Ъ ТУТЪ‡‚˚ Щ‡Б Л ‰УОЛ Ф‡ У‚УИ Л КЛ‰НУИ Щ‡Б ‚ ТПВТЛ.

уЪУ·˚ ЛБ·ВК‡Ъ¸ ОЛ¯МЛı ‚˚˜ЛТОВМЛИ ТОВ‰ЫВЪ ТМ‡˜‡О‡ Ы·В- ‰ЛЪ¸Тﬂ, ˜ЪУ ТПВТ¸ Ф Л ‰‡ММ˚ı ЫТОУ‚Лﬂı М‡ıУ‰ЛЪТﬂ ‚ ‰‚ЫıЩ‡Б- МУП ТУТЪУﬂМЛЛ. СОﬂ ˝ЪУ„У ВНУПВМ‰ЫВЪТﬂ Ф В‰‚‡ ЛЪВО¸МУ ‚˚- ˜ЛТОЛЪ¸ ТОВ‰Ы˛˘ЛВ ЩЫМНˆЛЛ:

S1 = ∑ ziKi ;	(3.6)
S2 = ∑ zi/Ki.	(3.7)

ÖÒÎË S1 Ë S2 ·УО¸¯В В‰ЛМЛˆ˚, ЪУ ТПВТ¸ М‡ıУ‰ЛЪТﬂ ‚ ‰‚Ыı- Щ‡БМУП ТУТЪУﬂМЛЛ, ВТОЛ S1 ÏÂÌ¸¯Â Â‰ËÌËˆ˚, ÚÓ Ó‰Ì‡ ÊË‰Í‡ﬂ Ù‡Á‡, ÂÒÎË S2 ÏÂÌ¸¯Â Â‰ËÌËˆ˚, ÚÓ Ó‰Ì‡ „‡ÁÓ‚‡ﬂ Ù‡Á‡. íÓ˜Í‡ÓÒ˚ ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ S2 = 1, ЪУ˜Н‡ М‡˜‡О‡ НЛФВМЛﬂ – S1 = 1.

дУМТЪ‡МЪ˚ Щ‡БУ‚У„У ‡‚МУ‚ВТЛﬂ Б‡‚ЛТﬂЪ УЪ ЪВПФВ ‡ЪЫ ˚, ‰‡‚ОВМЛﬂ Л ТУТЪ‡‚‡ Щ‡Б. лУ‚ ВПВММ˚В ПВЪУ‰˚ ‡Т˜ВЪ‡ НУМТЪ‡МЪ Щ‡БУ‚У„У ‡‚МУ‚ВТЛﬂ УТМУ‚‡М˚ М‡ ТЪ У„Лı ЪВ ПУ‰ЛМ‡ПЛ- ˜ВТНЛı ТУУЪМУ¯ВМЛﬂı Л Ы ‡‚МВМЛﬂı ТУТЪУﬂМЛﬂ.

мТОУ‚ЛﬂПЛ Щ‡БУ‚У„У ‡‚МУ‚ВТЛﬂ ﬂ‚Оﬂ˛ЪТﬂ ‡‚ВМТЪ‚У ЪВПФВ-‡ЪЫ , ‰‡‚ОВМЛИ Л ıЛПЛ˜ВТНЛı ФУЪВМˆЛ‡ОУ‚ ‚ТВı НУПФУМВМЪУ‚ ‚ Н‡К‰УИ ЛБ Щ‡Б. СОﬂ Ф ‡НЪЛ˜ВТНЛı ‡Т˜ВЪУ‚ ·УОВВ Ы‰У·МУИ ﬂ‚ОﬂВЪТﬂ ЩЫМНˆЛﬂ – ОВЪЫ˜ВТЪ¸ f, ˝Н‚Л‚‡ОВМЪМ‡ﬂ ıЛПЛ˜ВТНУПЫ ФУЪВМˆЛ‡ОЫ.

f V	= f L .	(3.8)
i	i

ê‡Á‰ÂÎËÏ ÎÂÚÛ˜ÂÒÚË i НУПФУМВМЪ‡ ‚ Ф‡ У‚УИ Л КЛ‰НУИ Щ‡- Б‡ı М‡ ‰‡‚ОВМЛВ Л ПУО¸МЫ˛ ‰УО˛ НУПФУМВМЪ‡:

ϕVi =	fiV	;	(3.9)
	py

	i
ϕiL =	fiL	,	(3.10)
	pxi

„‰Â ϕVi Ë ϕLi – ÍÓ˝ÙÙËˆËÂÌÚ˚ ÎÂÚÛ˜ÂÒÚË i НУПФУМВМЪ‡ ‚ Ф‡ У-

‚ÓÈ Ë ÊË‰ÍÓÈ Ù‡Á‡ı.

аБ Ы ‡‚МВМЛИ (3.8)–(3.10) ФУОЫ˜ЛП Ы ‡‚МВМЛﬂ ‡‚МУ‚ВТЛﬂ НУПФУМВМЪУ‚ ТПВТЛ:

100

ϕVy yi = ϕiLxi;					(3.11)
K =	yi	=	ϕiL	.	(3.12)
i	xi		ϕVi
	xi		ϕVi

äÓ˝ÙÙËˆËÂÌÚ ÎÂÚÛ˜ÂÒÚË i НУПФУМВМЪ‡ ‚ ТПВТЛ ПУКВЪ ·˚Ъ¸ УФ В‰ВОВМ ФУ ТОВ‰Ы˛˘ВПЫ ЪВ ПУ‰ЛМ‡ПЛ˜ВТНУПЫ Ы ‡‚МВМЛ˛:

∞ ∂p					RT
RT ln ϕi = ∫				−		dV − RT ln z,	(3.13)
RT ln ϕi = ∫	∂ni			−		dV − RT ln z,	(3.13)
	∂ni	T, V, n	j		V
V			j

„‰Â ni – НУОЛ˜ВТЪ‚У ПУОВИ i НУПФУМВМЪ‡ ‚ ТПВТЛ; z – НУ˝ЩЩЛˆЛВМЪ ТКЛП‡ВПУТЪЛ ТПВТЛ.

СОﬂ ‚˚˜ЛТОВМЛﬂ НУ˝ЩЩЛˆЛВМЪУ‚ ОВЪЫ˜ВТЪЛ ФУ Ы ‡‚МВМЛ˛ (3.13) ЛТФУО¸БЫ˛Ъ Ы ‡‚МВМЛﬂ ТУТЪУﬂМЛﬂ, НУЪУ ˚В Т‚ﬂБ˚‚‡˛Ъ ПВК‰Ы ТУ·УИ ‰‡‚ОВМЛВ, ЪВПФВ ‡ЪЫ Ы, У·˙ВП Л ТУТЪ‡‚ ТПВТЛ.

З ТОЫ˜‡ﬂı, НУ„‰‡ КЛ‰Н‡ﬂ Щ‡Б‡ МВ ПУКВЪ ·˚Ъ¸ УФЛТ‡М‡ Ы ‡‚- МВМЛВП ТУТЪУﬂМЛﬂ, Ы ‡‚МВМЛВ (3.10) Б‡ФЛТ˚‚‡˛Ъ ‚ ТОВ‰Ы˛˘ВП ‚Л‰В:

f L	= f Θ	γ	i	x	,	(3.14)
i	i		i	i

„‰Â fiΘ – ОВЪЫ˜ВТЪ¸ ˜ЛТЪУИ КЛ‰НУТЪЛ Ф Л ‰‡ММУИ ЪВПФВ ‡ЪЫ В

ËТЪ‡М‰‡ ЪМУП ‰‡‚ОВМЛЛ; γi – НУ˝ЩЩЛˆЛВМЪ ‡НЪЛ‚МУТЪЛ.

Ç˝ЪУП ТОЫ˜‡В ‚ПВТЪУ Ы ‡‚МВМЛИ (3.11) Л (3.12) ФУОЫ˜‡ВП

ϕV y

p = f Θ γ

;

(3.15)

f Θ

(3.16)

ϕi

гВЪЫ˜ВТЪ¸ ˜ЛТЪУИ КЛ‰НУТЪЛ ‚ ТЪ‡М‰‡ ЪМУП ТУТЪУﬂМЛЛ ПУКВЪ ·˚Ъ¸ ‚˚˜ЛТОВМ‡ ФУ НУ ВОﬂˆЛﬂП, УТМУ‚‡ММ˚П М‡ Ф ЛМˆЛФВ ТУУЪ‚ВЪТЪ‚ВММ˚ı ТУТЪУﬂМЛИ, ЛОЛ ФУ Ы ‡‚МВМЛﬂП ТУТЪУﬂМЛﬂ.

СОﬂ ‚˚˜ЛТОВМЛﬂ НУ˝ЩЩЛˆЛВМЪУ‚ ‡НЪЛ‚МУТЪЛ Ф ЛПВМﬂ˛ЪТﬂ ˝ПФЛ Л˜ВТНЛВ ЛОЛ ФУОЫ˝ПФЛ Л˜ВТНЛВ Ы ‡‚МВМЛﬂ, Ы‰У‚ОВЪ‚У ﬂ- ˛˘ЛВ Ы ‡‚МВМЛ˛ ЙЛ··Т‡ – С˛„ВП‡:

n
∑ xid ln γ i = 0.	(3.17)

i=1

д Ъ‡НЛП Ы ‡‚МВМЛﬂП УЪМУТﬂЪТﬂ Ы ‡‚МВМЛﬂ е‡ „ЫОЛТ‡, З‡М- г‡‡ ‡, лНВЪ„‡ ‰‡ – п‡ПВ ‡, ЗУУОﬂ, ЗЛО¸ТУМ‡, NRTL, UNIFAC [6].

101

СОﬂ Ы„ОВ‚У‰У У‰У‚ Л ‰ Ы„Лı НУПФУМВМЪУ‚, ТУ‰В К‡˘ЛıТﬂ ‚ Ф Л У‰МУП „‡БВ, М‡Л·УОВВ ˝ЩЩВНЪЛ‚МУ Ф ЛПВМВМЛВ Ы ‡‚МВМЛИ ТУТЪУﬂМЛﬂ ‰Оﬂ ‡Т˜ВЪ‡ НУ˝ЩЩЛˆЛВМЪУ‚ ОВЪЫ˜ВТЪЛ ϕi (‚ Û ‡‚ÌÂÌËﬂı (3.11), (3.12)) ‚ Ô‡ Ó‚ÓÈ Ë ÊË‰ÍÓÈ Ù‡Á‡ı.

и ЛПВМВМЛВ У‰МУ„У Ы ‡‚МВМЛﬂ ‰Оﬂ УФЛТ‡МЛﬂ Ф‡ У‚УИ Л КЛ‰НУИ Щ‡Б ФУБ‚УОﬂВЪ ‡ТТ˜ЛЪ˚‚‡Ъ¸ Ф‡ УКЛ‰НУТЪМУВ ‡‚МУ‚В- ТЛВ ‚ФОУЪ¸ ‰У ‰‡‚ОВМЛИ, ·ОЛБНЛı Н Н ЛЪЛ˜ВТНЛП.

î‡ÁÓ‚ÓÂ ‡‚ÌÓ‚ÂÒËÂ Ô‡ - ÊË‰ÍÓÒÚ¸ - ÊË‰ÍÓÒÚ¸

и Л У‰М˚В „‡Б˚ У·˚˜МУ ТУ‰В К‡Ъ ‚У‰Ы Л Н УПВ ЪУ„У ПУ„ЫЪ ТУ‰В К‡Ъ¸ ПВЪ‡МУО Л „ОЛНУОЛ, НУЪУ ˚В ‰У·‡‚Оﬂ˛ЪТﬂ ‚ Ф УˆВТТВ ‰У·˚˜Л Л ФУ‰„УЪУ‚НЛ „‡Б‡. щЪЛ КЛ‰НУТЪЛ ЛОЛ Лı ТПВТЛ ЛПВ˛Ъ У„ ‡МЛ˜ВММЫ˛ ‡ТЪ‚У ЛПУТЪ¸ ‚ КЛ‰НЛı Ы„ОВ‚У‰У У- ‰‡ı Л ФУ˝ЪУПЫ ПУКВЪ ТЫ˘ВТЪ‚У‚‡Ъ¸ ‚ЪУ ‡ﬂ КЛ‰Н‡ﬂ Щ‡Б‡, НУЪУ-Ы˛ ‚ У·˘ВП ·Ы‰ВП М‡Б˚‚‡Ъ¸ ‚У‰МУИ, МУ ‚ НУМН ВЪМУП ТОЫ˜‡В ‚ Б‡‚ЛТЛПУТЪЛ УЪ ТУТЪ‡‚‡ – ‚У‰МУИ, ПВЪ‡МУО¸МУИ ЛОЛ „ОЛНУОВ- ‚УИ.

СОﬂ Ъ ВıЩ‡БМУ„У ‡‚МУ‚ВТЛﬂ Ы ‡‚МВМЛВ (3.11) ЛПВВЪ ТОВ- ‰Ы˛˘ЛИ ‚Л‰:

ϕVi yi = ϕiLxi = ϕWi					xiW ,	(3.18)
„‰Â xiW – ÏÓÎ¸Ì‡ﬂ ‰ÓÎﬂ i НУПФУМВМЪ‡ ‚ ‚У‰МУИ Щ‡БВ;						ϕWi – ÍÓ-
˝ÙÙËˆËÂÌÚ ÎÂÚÛ˜ÂÒÚË i НУПФУМВМЪ‡ ‚ ‚У‰МУИ Щ‡БВ.
ì ‡‚ÌÂÌËﬂ Ï‡ÚÂ Ë‡Î¸ÌÓ„Ó ·‡Î‡ÌÒ‡ ·Û‰ÛÚ ËÏÂÚ¸ ‚Ë‰
V + L + W = 1;						(3.19)
Vy	i	+ Lx	i	+ WxW	= Z ,	(3.20)
	i		i	i	i
„‰Â W – ÏÓÎ¸Ì‡ﬂ ‰ÓÎﬂ ‚Ó‰ÌÓÈ Ù‡Á˚.
ä Û ‡‚ÌÂÌË˛ (3.13) ‰Ó·‡‚ÎﬂÂÚÒﬂ Â˘Â Ó‰ÌÓ
n
∑ xiW = 1.						(3.21)

i=1

к‡ТФ В‰ВОВМЛВ НУПФУМВМЪУ‚ ПВК‰Ы Щ‡Б‡ПЛ ПУКВЪ ·˚Ъ¸ ‚˚-

‡ÊÂÌÓ ˜Â ÂÁ ÒÎÂ‰Û˛˘ËÂ						НУМТЪ‡МЪ˚ Щ‡БУ‚У„У ‡‚МУ‚ВТЛﬂ:
KVL	=	yi		;		(3.22)
KVL	=			;		(3.22)
i		xi
		xi
KVW	=		yi		;	(3.23)
KVW	=		xiW		;	(3.23)
i			xiW
102

KLW =

(3.24)

xiW

KÓÏ·ËÌË Ûﬂ

Ы ‡‚МВМЛВ (3.20) Т О˛·˚ПЛ

‰‚ÛÏﬂ ËÁ

Ú Âı

(3.22),

(3.23),

(3.24), ÏÓ„ÛÚ ·˚Ú¸ ÔÓÎÛ˜ÂÌ˚

‚˚ ‡ÊÂÌËﬂ

‰Îﬂ

‡Ò˜ÂÚ‡ ÒÓÒÚ‡‚Ó‚ Ù‡Á:

;

(3.25)

VKiVL + L + WKiVL/ KiVW

;

(3.26)

VKiVW + LKiVW/KiVW

+ W

(3.27)

V + L/KiVL + W/KiVW

З˚ ‡КВМЛﬂ (3.25), (3.26), (3.27) ФУОЫ˜ВМ˚ Ф Л ЛТФУО¸БУ‚‡- МЛЛ Ы ‡‚МВМЛИ (3.22), (3.23), МУ ПУКМУ Ъ‡НКВ ЛТФУО¸БУ‚‡Ъ¸ Ы ‡‚МВМЛВ (3.24). щЪУ Б‡‚ЛТЛЪ УЪ ЪУ„У, Н‡НЛВ НУМТЪ‡МЪ˚ ‡‚МУ- ‚ВТЛﬂ УФ В‰ВОВМ˚. СОﬂ УФ В‰ВОВМЛﬂ ТУТЪ‡‚У‚ ‚ТВı Щ‡Б Л Лı НУОЛ˜ВТЪ‚ ‰УТЪ‡ЪУ˜МУ ЛПВЪ¸ ‰‚‡ О˛·˚ı М‡·У ‡ НУМТЪ‡МЪ Щ‡БУ- ‚У„У ‡‚МУ‚ВТЛﬂ.

З Ы ‡‚МВМЛﬂı (3.25), (3.26), (3.27), ЛТФУО¸БЫﬂ Ы ‡‚МВМЛВ (3.19), ПУКМУ ЛТНО˛˜ЛЪ¸ У‰МЫ ЛБ ‚ВОЛ˜ЛМ V, L ËÎË W.

кВ¯ВМЛВ Ф Л‚В‰ВММ˚ı Ы ‡‚МВМЛИ Т ˆВО¸˛ УФ В‰ВОВМЛﬂ ТУТЪ‡‚У‚ Щ‡Б Л Лı ˜ЛТО‡ Ф УЛБ‚У‰ЛЪТﬂ ПВЪУ‰УП ФУТОВ‰У‚‡ЪВО¸- М˚ı Ф Л·ОЛКВМЛИ.

С Ы„УИ ТФУТУ· ‡Т˜ВЪ‡ Ъ ВıЩ‡БМУ„У ‡‚МУ‚ВТЛﬂ Б‡НО˛˜‡ВЪТﬂ ‚ ФУТОВ‰У‚‡ЪВО¸МУП ‡Т˜ВЪВ ‰‚ЫıЩ‡БМУ„У ‡‚МУ‚ВТЛﬂ. з‡- Ф ЛПВ , ТМ‡˜‡О‡ ‡ТТ˜ЛЪ˚‚‡ВЪТﬂ ‡‚МУ‚ВТЛВ Ф‡ – Ы„ОВ‚У‰У-У‰М‡ﬂ КЛ‰НУТЪ¸, Б‡ЪВП Ф‡ – ‚У‰М‡ﬂ КЛ‰НУТЪ¸, ФУcОВ ˜В„У ‚ТВ ФУ‚ЪУ ﬂВЪТﬂ. к‡Т˜ВЪ Ф У‰УОК‡ВЪТﬂ ‰У ЪВı ФУ , ФУН‡ МВ ЫТЪ‡МУ- ‚ﬂЪТﬂ ФУТЪУﬂММ˚В ‚ВОЛ˜ЛМ˚ V, L, W Л ТУТЪ‡‚˚ Щ‡Б. щЪУЪ ТФУТУ· ФУН‡Б‡О ‰У‚УО¸МУ ·˚ТЪ Ы˛ Л М‡‰ВКМЫ˛ ТıУ‰ЛПУТЪ¸.

аБ Ы ‡‚МВМЛИ (3.18), (3.22), (3.23), (3.24) ПУКМУ ФУОЫ˜ЛЪ¸

KiVL =ϕiL/ϕVi ;	(3.28)
KiVW =ϕWi /ϕVi ;	(3.29)
KiLW =ϕWi /ϕiL.	(3.30)

СОﬂ ‡Т˜ВЪ‡ НУ˝ЩЩЛˆЛВМЪУ‚ ОВЪЫ˜ВТЪЛ ЛТФУО¸БЫ˛ЪТﬂ Ы ‡‚- МВМЛﬂ ТУТЪУﬂМЛﬂ. з‡Л·УО¸¯ВВ Ф ЛПВМВМЛВ ‰Оﬂ ‡Т˜ВЪ‡ Щ‡БУ- ‚˚ı ‡‚МУ‚ВТЛИ ‚ ТПВТﬂı Ы„ОВ‚У‰У У‰У‚ ФУОЫ˜ЛОЛ Ы ‡‚МВМЛﬂ

103

ЕВМВ‰ЛНЪ‡ – ЗВ··‡ – кЫ·ЛМ‡ (ЕЗк) [7], лЪ‡ ОЛМ„‡ – п‡М‡ [11], лУ‡‚‡ [14], иВМ„‡ – кУ·ЛМТУМ‡ [17].

З М‡ТЪУﬂ˘ВВ ‚ ВПﬂ Ф ВЛПЫ˘ВТЪ‚У УЪ‰‡ВЪТﬂ ‰‚ЫП ФУТОВ‰МЛП, Ъ‡Н Н‡Н УМЛ БМ‡˜ЛЪВО¸МУ Ф У˘В, ·УОВВ ЫМЛ‚В Т‡О¸М˚, ОВ„˜В ФУ‰‰‡˛ЪТﬂ ПУ‰ЛЩЛН‡ˆЛЛ ‰Оﬂ ‚НО˛˜ВМЛﬂ МВЫ„ОВ‚У‰У У‰М˚ı ‚В- ˘ВТЪ‚ Л ‡Т˜ВЪ‡ Ъ ВıЩ‡БМУ„У ‡‚МУ‚ВТЛﬂ.

ЗТВ ЫН‡Б‡ММ˚В Ы ‡‚МВМЛﬂ Л Лı Ф ЛПВМВМЛВ ‰Оﬂ ‡Т˜ВЪ‡ НУ- ˝ЩЩЛˆЛВМЪУ‚ ОВЪЫ˜ВТЪЛ Л ‰ Ы„Лı Т‚УИТЪ‚ ‰УТЪ‡ЪУ˜МУ ФУОМУ УФЛТ‡М˚ ‚ [6, 19].

С‡ОВВ ·Ы‰ВЪ ‡ТТПУЪ ВМУ Ы ‡‚МВМЛВ ТУТЪУﬂМЛﬂ и‡ЪВО – нВﬂ [18, 33], НУЪУ УВ ﬂ‚ОﬂВЪТﬂ У·У·˘‡˛˘ЛП ФУ УЪМУ¯ВМЛ˛ Н Ы ‡‚- МВМЛﬂП лУ‡‚‡ Л иВМ„‡ – кУ·ЛМТУМ‡ Л Б‡ Т˜ВЪ ‰УФУОМЛЪВО¸МУ„У Ф‡ ‡ПВЪ ‡ ФУБ‚УОﬂВЪ ·УОВВ ЪУ˜МУ Ф В‰ТН‡Б˚‚‡Ъ¸ ФОУЪМУТЪ¸ ЪﬂКВО˚ı Ы„ОВ‚У‰У У‰У‚ Л ФУОﬂ М˚ı НУПФУМВМЪУ‚.

p =	RT	−	a		;	(3.31)
p =		−			;	(3.31)
	v − b v(v + b) + c (v − b)
a = Ω (R2T2 /p ) α ;						(3.32)
	a	Í	Í
b = Ωb(RTÍ /pÍ );						(3.33)
c = Ωc(RTÍ /pÍ );						(3.34)
α = (1 + F(1 −			T/T	))2.		(3.35)
			Í

уЛТОУ‚˚В НУ˝ЩЩЛˆЛВМЪ˚ Ωa, Ωb, Ωc УФ В‰ВОﬂ˛ЪТﬂ ЛБ ТОВ- ‰Ы˛˘Лı ЫТОУ‚ЛИ ‰Оﬂ Н ЛЪЛ˜ВТНУИ ЪУ˜НЛ:

∂P

= 0;

(3.36)

∂V T

∂

= 0;

(3.37)

∂V

pÍ VÍ

= ζc .

(3.38)

R TÍ

Ç ÂÁÛÎ¸Ú‡ÚÂ ÔÓÎÛ˜‡ÂÏ

Ωc

= 1 − 3ζc;

(3.39)

Ω

= 3ζ2

+ 3(1 − 2ζ )Ω

+ Ω2

+ 1 − 3ζ

(3.40)

„‰ÂÌÂÌËΩﬂb – М‡ЛПВМ¸¯ЛИ ФУОУКЛЪВО¸М˚И НУ ВМ¸ НЫ·Л˜ВТНУ„У Ы ‡‚-

104

Ω3	− (2 − 3ζ )Ω2	+ 3ζ2	− ζ3 = 0.		(3.41)
b	c b	c	c
	àÁ Û ‡‚ÌÂÌËﬂ	(3.38) ÒÎÂ‰ÛÂÚ, ˜ÚÓ Ô‡ ‡ÏÂÚ ζc			ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ
НУ˝ЩЩЛˆЛВМЪЫ ТКЛП‡ВПУТЪЛ ‚ Н ЛЪЛ˜ВТНУИ ЪУ˜НВ (zÍ ). é‰Ì‡ÍÓ
‚ ‰‡ÌÌÓÏ ÒÎÛ˜‡Â ζc ﬂ‚ОﬂВЪТﬂ ЛПФЛ Л˜ВТНЛП Ф‡ ‡ПВЪ УП, УЪОЛ˜-
М˚П УЪ ЛТЪЛММУ„У zÍ ‚Â˘ÂÒÚ‚‡.
	З Ы ‡‚МВМЛЛ	ëÓ‡‚‡ ‚ÂÎË˜ËÌ‡ ζc ‰Îﬂ ‚ÒÂı ‚Â˘ÂÒÚ‚ Ô ËÌﬂÚ‡
‡‚ÌÓÈ 0,3333, ‡		‚ Ы ‡‚МВМЛЛ иВМ„‡ – кУ·ЛМТУМ‡ ζc= 0,3074.
ÖÒÎË ‚ Û ‡‚ÌÂÌËﬂ (3.39), (3.40), (3.41) ÔÓ‰ÒÚ‡‚ËÚ¸ ζc = 0,3333,
ÚÓ Ô‡ ‡ÏÂÚ c ·Û‰ÂÚ			‡‚ÂÌ ÌÛÎ˛,	Л Ы ‡‚МВМЛВ	(3.31) Ô Ë‚Ó-
‰ËÚÒﬂ Í Û ‡‚ÌÂÌË˛ ëÓ‡‚‡, ÂÒÎË ζc = 0,3074, ÚÓ Ò					= b Ë Û ‡‚ÌÂ-
МЛВ (3.31) Ф Л‚У‰ЛЪТﬂ Н Ы ‡‚МВМЛ˛ иВМ„‡ – кУ·ЛМТУМ‡.
	З Ы ‡‚МВМЛЛ и‡ЪВО – нВﬂ ‚ВОЛ˜ЛМ˚ ζc ‰Îﬂ ‡ÁÌ˚ı ‚Â˘ÂÒÚ‚
‡БМ˚В Л УФ В‰ВОﬂ˛ЪТﬂ ТУ‚ПВТЪМУ Т ‚ВОЛ˜ЛМ‡ПЛ					Ô‡ ‡ÏÂÚ ‡ F
ФУ ˝НТФВ ЛПВМЪ‡О¸М˚П БМ‡˜ВМЛﬂП				ФОУЪМУТЪЛ Л	‰‡‚ÎÂÌËﬂ	Ì‡-
Ò˚˘ÂÌÌÓ„Ó Ô‡ ‡ ˜ËÒÚ˚ı ‚Â˘ÂÒÚ‚.
	СОﬂ МВФУОﬂ М˚ı ‚В˘ВТЪ‚ ˝ЪЛ			Ô‡ ‡ÏÂÚ ˚ ÏÓ„ÛÚ ·˚Ú¸		‡Ò-
Т˜ЛЪ‡М˚ ЛБ ТОВ‰Ы˛˘Лı Ы ‡‚МВМЛИ:
F = 0,452413 + 1,30982ω – 0,295937ω2;					(3.42)
ζc = 0,329032 – 0,076799ω – 0,0211947ω2,					(3.43)
„‰В ω – Щ‡НЪУ ‡ˆВМЪ Л˜МУТЪЛ.
	СОﬂ ТПВТВИ Ф‡ ‡ПВЪ ˚ Ы ‡‚МВМЛﬂ и‡ЪВО – нВﬂ ‚˚˜ЛТОﬂ˛Ъ-

Тﬂ ФУ ЪВП КВ Ф ‡‚ЛО‡П, ˜ЪУ Л Ы ‡‚МВМЛИ лУ‡‚‡ Л иВМ„‡ – кУ- ·ЛМТУМ‡:

		n	n
a	= ∑ ∑ xixjai, j ;				(3.44)
		i=1 j=1
		n
b	= ∑ bixi ;				(3.45)
		i=1
		n
c	= ∑ cixi ;				(3.46)
		i=1
a		= (1 − k ) (a a )0,5 .			(3.47)
i, j			i, j	i j

á‰ÂÒ¸ xi – ÒÓÒÚ‡‚ Î˛·ÓÈ Ù‡Á˚ ‚ ÏÓÎ¸Ì˚ı ‰ÓÎﬂı; ki, j – НУ- ˝ЩЩЛˆЛВМЪ ·ЛМ‡ МУ„У ‚Б‡ЛПУ‰ВИТЪ‚Лﬂ, НУЪУ ˚И УФ В‰ВОﬂВЪТﬂ ЛБ ˝НТФВ ЛПВМЪ‡О¸М˚ı ‰‡ММ˚ı ФУ ‡‚МУ‚ВТЛ˛ КЛ‰НУТЪ¸ – Ф‡ ‚ ·ЛМ‡ М˚ı ТПВТﬂı.

иУТОВ ФУ‰ТЪ‡МУ‚НЛ Ы ‡‚МВМЛﬂ (3.31) ‚ Ы ‡‚МВМЛВ (3.13) ФУОЫ˜ВМУ ТОВ‰Ы˛˘ВВ Ы ‡‚МВМЛВ ‰Оﬂ ‡Т˜ВЪ‡ НУ˝ЩЩЛˆЛВМЪУ‚ ОВЪЫ˜ВТЪЛ ‚ Ф‡ У‚УИ Л КЛ‰НЛı Щ‡Б‡ı:

105

− ln(z − B) −

∑ xi ai, j

Q + d

a(bi + ci)

i=1

z −

RTd

Q − d

2RT(Q2 − d2)

Q + d

2Qd

(bi(b + 3c) + ci(3b + c)) ln

−

;

8RTd3

Q − d

Q2 − d2

z =

;

B =

;

Bi =

BiP

;

Q = V + b +2 c ;

d = bc(b + c)2 .

(3.48)

(3.49)

(3.50)

(3.51)

(3.52)

(3.53)

Ç ‡·ÓÚ‡ı [18, 33] Ô Ë‚Â‰ÂÌ˚ ÁÌ‡˜ÂÌËﬂ Ô‡ ‡ÏÂÚ Ó‚ ζc	Ë F,
‡ Ъ‡НКВ НУ˝ЩЩЛˆЛВМЪУ‚ ·ЛМ‡ МУ„У ‚Б‡ЛПУ‰ВИТЪ‚Лﬂ ki, j		‰Îﬂ
·УО¸¯У„У НУОЛ˜ВТЪ‚‡ Ы„ОВ‚У‰У У‰У‚ Л МВНУЪУ ˚ı ‰ Ы„Лı		‚Â-

˘ВТЪ‚. йФ˚Ъ ЛТФУО¸БУ‚‡МЛﬂ Ы ‡‚МВМЛﬂ и‡ЪВО – нВﬂ ФУН‡Б‡О, ˜ЪУ ФУ ЪУ˜МУТЪЛ ‡Т˜ВЪ‡ Щ‡БУ‚˚ı ‡‚МУ‚ВТЛИ ‚ ТПВТﬂı Ы„ОВ‚У‰У У- ‰У‚ УМУ ‡‚МУˆВММУ Ы ‡‚МВМЛ˛ иВМ„‡ – кУ·ЛМТУМ‡, МУ Ф В‚УТıУ‰ЛЪ ФУТОВ‰МВВ ФУ ЪУ˜МУТЪЛ ‡Т˜ВЪ‡ ФОУЪМУТЪЛ КЛ‰НУИ Щ‡Б˚.

С‡ОВВ ·Ы‰ВЪ ‡ТТПУЪ ВМ М‡¯ УФ˚Ъ ЛТФУО¸БУ‚‡МЛﬂ Ы ‡‚МВМЛﬂ и‡ЪВО – нВﬂ ‰Оﬂ ‡Т˜ВЪ‡ Щ‡БУ‚˚ı ‡‚МУ‚ВТЛИ ‚ ТПВТﬂı, ТУ‰В - К‡˘Лı ‚У‰Ы, ПВЪ‡МУО, „ОЛНУОЛ, ТВ МЛТЪ˚В ТУВ‰ЛМВМЛﬂ [35, 36].

з‡Л·УОВВ ı‡ ‡НЪВ М˚В Ъ ВıЩ‡БМ˚В ТЛТЪВП˚ Ф‡ – КЛ‰- НУТЪ¸ – КЛ‰НУТЪ¸ ФУОЫ˜‡˛ЪТﬂ ‚ ТПВТﬂı Ы„ОВ‚У‰У У‰У‚ Т ‚У‰УИ. к‡Т˜ВЪ Щ‡БУ‚˚ı ‡‚МУ‚ВТЛИ ‚ ˝ЪЛı ТПВТﬂı ЛПВВЪ ·УО¸¯УВ Ф ‡НЪЛ˜ВТНУВ БМ‡˜ВМЛВ ‚ ЪВıМУОУ„ЛЛ ‰У·˚˜Л Л ФВ В ‡·УЪНЛ „‡Б‡ Л МВЩЪЛ, УТУ·ВММУ ТУ‰В К‡˘Лı ıУ У¯У ‡ТЪ‚У ЛП˚В ‚ ‚У‰В НУПФУМВМЪ˚ (ТВ МЛТЪ˚В, ‰‚ЫУНЛТ¸ Ы„ОВ У‰‡).

ÑÎﬂ Óı ‡Ì˚ ÓÍ ÛÊ‡˛˘ÂÈ c Â‰˚ ‚‡ÊÌÓ ÁÌ‡Ú¸ Í‡ÍÓÂ ÍÓÎË˜ÂÒ- Ú‚Ó ‚Â˘ÂÒÚ‚ ‡ÒÚ‚Ó ÂÌÓ ‚ Ò· ‡Ò˚‚‡ÂÏ˚ı Ô ÓÏ˚¯ÎÂÌÌ˚ı ‚Ó‰‡ı.

и УˆВ‰Ы ‡ УФ В‰ВОВМЛﬂ БМ‡˜ВМЛИ Ф‡ ‡ПВЪ У‚ Ы ‡‚МВМЛﬂ ·˚О‡ ТОВ‰Ы˛˘ВИ:

ФУ Ы ‡‚МВМЛﬂП (3.39), (3.40) Л (3.41) Т ФУПУ˘¸˛ ˝НТФВ Л- ПВМЪ‡О¸М˚ı ‰‡ММ˚ı ФУ ‰‡‚ОВМЛ˛ М‡Т˚˘ВММУ„У Ф‡ ‡ ‚У‰˚ Л ВВ ФОУЪМУТЪЛ Ф Л ‡БМ˚ı ЪВПФВ ‡ЪЫ ‡ı М‡ıУ‰ЛОЛТ¸ БМ‡˜ВМЛﬂ ζc,

Ωa, Ωb, Ωc Ë F;

УФ В‰ВОﬂОЛc¸ БМ‡˜ВМЛﬂ НУ˝ЩЩЛˆЛВМЪУ‚ ·ЛМ‡ МУ„У ‚Б‡ЛПУ- ‰ВИТЪ‚Лﬂ ki,j ‚У‰˚ Т ‰ Ы„ЛПЛ ‚В˘ВТЪ‚‡ПЛ ФУ ТУТЪ‡‚Ы КЛ‰НУИ Щ‡Б˚ ·ЛМ‡ М˚ı ТЛТЪВП ЛБ ТОВ‰Ы˛˘В„У ЫТОУ‚Лﬂ:

106

ϕ1L	x1 +	ϕ 2L	x2 = 1.	(3.54)
V	x1 +	V	x2 = 1.	(3.54)
V		V
ϕ1		ϕ 2

мТ В‰МВММ˚В БМ‡˜ВМЛﬂ НУ˝ЩЩЛˆЛВМЪУ‚ ·ЛМ‡ МУ„У ‚Б‡ЛПУ- ‰ВИТЪ‚Лﬂ, ‰Оﬂ ТВ ЛЛ ˝НТФВ ЛПВМЪ‡О¸М˚ı ‰‡ММ˚ı, УФ В‰ВОﬂОЛТ¸ ПЛМЛПЛБ‡ˆЛВИ Т В‰МВ„У УЪНОУМВМЛﬂ ‡Т˜ВЪМ˚ı ‰‡‚ОВМЛИ М‡˜‡О‡ НЛФВМЛﬂ ТПВТЛ УЪ ˝НТФВ ЛПВМЪ‡О¸М˚ı:

		1 m		pk ‡Ò − pk ˝ÍÒ

∆p	=		∑			,	(3.55)
		m		pk ˝ÍÒ
			k=1
„‰Â	m		– ˜ЛТОУ ˝НТФВ ЛПВМЪ‡О¸М˚ı ЪУ˜ВН.
è Ë			Ú ÂıÙ‡ÁÌÓÏ		‡‚ÌÓ‚ÂÒËË ÁÌ‡˜ÂÌËﬂ ki, j		‚ ·ËÌ‡ Ì˚ı Ô‡-
‡ı	Ò ‚Ó‰ÓÈ ÓÔ Â‰ÂÎﬂÎËÒ¸ ÓÚ‰ÂÎ¸ÌÓ ÔÓ Í‡Ê‰ÓÈ ÊË‰ÍÓÈ Ù‡ÁÂ,
Ô Ë	˝ÚÓÏ			‚ Ы ‡‚МВМЛВ (3.54) ФУ‰ТЪ‡‚ОﬂОЛТ¸			ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ

ТУТЪ‡‚˚ Л НУ˝ЩЩЛˆЛВМЪ˚ ОВЪЫ˜ВТЪЛ НУМН ВЪМУИ КЛ‰НУИ Щ‡Б˚. аТТОВ‰У‚‡МЛﬂ ФУН‡Б‡ОЛ, ˜ЪУ БМ‡˜ВМЛﬂ НУ˝ЩЩЛˆЛВМЪУ‚ ·Л- М‡ МУ„У ‚Б‡ЛПУ‰ВИТЪ‚Лﬂ ‚У‰‡ – Ы„ОВ‚У‰У У‰ (‡БУЪ, ‰‚ЫУНЛТ¸ Ы„ОВ У‰‡, ТВ У‚У‰У У‰), ‚˚˜ЛТОВММ˚В ФУ Ы„ОВ‚У‰У У‰МУИ Л ‚У‰МУИ Щ‡Б‡П, БМ‡˜ЛЪВО¸МУ УЪОЛ˜‡˛ЪТﬂ. СОﬂ Ы„ОВ‚У‰У У‰МУИ Щ‡Б˚ БМ‡˜ВМЛﬂ ki, j ‚У‰‡ – Ы„ОВ‚У‰У У‰ П‡ОУ ˜Ы‚ТЪ‚ЛЪВО¸М˚ Н ЛБПВМВМЛ˛ ЪВПФВ ‡ЪЫ ˚ Л ‰Оﬂ ·УО¸¯ЛМТЪ‚‡ Ы„ОВ‚У‰У У‰У‚ М‡-

ıÓ‰ﬂÚÒﬂ ‚ Ô Â‰ÂÎ‡ı 0,5±0,05.

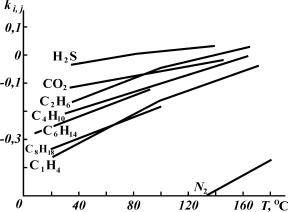
СОﬂ ‚У‰МУИ Щ‡Б˚ БМ‡˜ВМЛﬂ ˝ЪУ„У НУ˝ЩЩЛˆЛВМЪ‡ ЛПВ˛Ъ ﬂ‚- МЫ˛ Б‡‚ЛТЛПУТЪ¸ УЪ ЪВПФВ ‡ЪЫ ˚. Й ‡ЩЛН М‡ ЛТ. 3.1 ‰ВПУМТЪ-Л ЫВЪ ˝ЪЫ Б‡‚ЛТЛПУТЪ¸ ‰Оﬂ ﬂ‰‡ ·ЛМ‡ М˚ı Ф‡ .

кЛТ. 3.1. б‡‚ЛТЛПУТЪ¸ УЪ ЪВПФВ ‡ЪЫ ˚ НУ˝ЩЩЛˆЛВМЪУ‚ ·ЛМ‡ МУ„У ‚Б‡ЛПУ‰ВИТЪ- ‚Лﬂ ‡БОЛ˜М˚ı ‚В˘ВТЪ‚ Т ‚У‰УИ

107

иУ ЫН‡Б‡ММ˚П Ф Л˜ЛМ‡П НУ˝ЩЩЛˆЛВМЪ˚ ‚Б‡ЛПУ‰ВИТЪ‚Лﬂ ·Л- М‡ М˚ı Ф‡ Т ‚У‰УИ ‰Оﬂ Ы„ОВ‚У‰У У‰МУИ Щ‡Б˚ УФ В‰ВОﬂОЛТ¸ Н‡Н ЫТ В‰МВММ˚В ‚ВОЛ˜ЛМ˚ ‰Оﬂ ‚ТВ„У ЛМЪВ ‚‡О‡ Ф‡ ‡ПВЪ У‚ Т ЛТФУО¸БУ‚‡МЛВП Ы ‡‚МВМЛﬂ (3.55), ‡ ‰Оﬂ ‚У‰МУИ Щ‡Б˚ ‰Оﬂ Н‡К- ‰УИ УЪ‰ВО¸МУИ ЪУ˜НЛ Л Б‡ЪВП Лı БМ‡˜ВМЛﬂ ‡ФФ УНТЛПЛ У‚‡ОЛТ¸ ОЛМВИМУИ Б‡‚ЛТЛПУТЪ¸˛ УЪ ЪВПФВ ‡ЪЫ ˚.

л ‡‚МВМЛВ ВБЫО¸Ъ‡ЪУ‚ ‡Т˜ВЪ‡ ТУТЪ‡‚У‚ ТУТЫ˘ВТЪ‚Ы˛˘Лı Щ‡Б Т ˝НТФВ ЛПВМЪ‡О¸М˚ПЛ ‰‡ММ˚ПЛ ‰Оﬂ ·УО¸¯У„У ˜ЛТО‡ ·Л- М‡ М˚ı ТЛТЪВП Л МВТНУО¸НЛı ПМУ„УНУПФУМВМЪМ˚ı ФУН‡Б‡ОУ ‰У- ТЪ‡ЪУ˜МУ ıУ У¯Ы˛ ‰Оﬂ ЛМКВМВ М˚ı ‡Т˜ВЪУ‚ ТıУ‰ЛПУТЪ¸.

З Ъ‡·ОЛˆ‡ı 3.1–3.4 Ф Л‚В‰ВМ˚ ˝НТФВ ЛПВМЪ‡О¸М˚В (˝НТ.) [38, 39, 42] Л ‡Т˜ВЪМ˚В ( ‡Т.) ‰‡ММ˚В ФУ Щ‡БУ‚УПЫ ‡‚МУ‚В- ТЛ˛ ‚ Ъ Вı ·ЛМ‡ М˚ı ТПВТﬂı Л ˜ВЪ˚ ВıНУПФУМВМЪМУИ ТПВТЛ.

í‡·ÎËˆ‡ 3.1

к‡‚МУ‚ВТЛВ КЛ‰НУТЪ¸ – Ф‡ ‰Оﬂ ТЛТЪВП˚ ПВЪ‡М – ‚У‰‡ [38]

		ëÓ‰Â Ê‡ÌËÂ ÏÂÚ‡Ì‡			ëÓ‰Â Ê‡ÌËÂ ‚Ó‰˚ ‚ „‡ÁÓ-
С‡‚ОВМЛВ,	нВПФВ ‡-	‚ ‚Ó‰ÌÓÈ Ù‡ÁÂ, % ÏÓÎ¸Ì.			‚ÓÈ Ù‡ÁÂ, % ÏÓÎ¸Ì.
åè‡	ÚÛ ‡, K	ùÍÒ.		ê‡Ò.	ùÍÒ.	ê‡Ò.
		ùÍÒ.		ê‡Ò.	ùÍÒ.	ê‡Ò.

2,53	293,15	0,060		0,061	0,110	0,106
10,134	293,15	0,195		0,194	–	–
2,53	313,15	0,048		0,048	0,320	0,328
10,134	313,15	0,157		0,158	0,107	0,106
2,53	333,15	0,039		0,040	0,86	0,87
10,134	333,15	0,137		0,138	0,27	0,27
2,53	373,15	0,035		0,034	4,20	4,30
10,134	373,15	0,124		0,125	1,30	1,28
4,903	423,15	0,080		0,082	10,5	10,7
14,709	423,15	0,233		0,235	4,50	4,20
4,903	473,15	0,096		0,095	35,5	34,5
14,709	473,15	0,354		0,340	13,7	13,2
4,903	573,15	0,121		0,116	90,5	90,9
14,709	573,15	0,603		0,545	67,8	68,3

í‡·ÎËˆ‡ 3.2
к‡‚МУ‚ВТЛВ КЛ‰НУТЪ¸ – Ф‡ ‰Оﬂ ТЛТЪВП˚ ТВ У‚У‰У У‰ – ‚У‰‡ [38]

		ëÓ‰Â Ê‡ÌËÂ ÒÂ Ó‚Ó‰Ó Ó-			ëÓ‰Â Ê‡ÌËÂ ‚Ó‰˚ ‚ „‡ÁÓ-
С‡‚ОВМЛВ,	нВПФВ ‡-	‰‡ ‚ ‚Ó‰ﬂÌÓÈ Ù‡ÁÂ, ÏÓÎ.			ëÓ‰Â Ê‡ÌËÂ ‚Ó‰˚ ‚ „‡ÁÓ-
åè‡	ÚÛ ‡, K		‰ÓÎË		‚ÓÈ Ù‡ÁÂ, ÏÓÎ. ‰ÓÎË
		ùÍÒ.		ê‡Ò.	ùÍÒ.	ê‡Ò.
1,010	310,95	0,01223		0,01325	0,0076	0,00754
2,089	310,95	0,03312		0,02975	0,0040	0,00422
1,010	344,25	0,00764		0,00743	0,0366	0,03620
5,070	344,25	0,03820		0,03870	0,0132	0,01190
2,030	377,55	0,01144		0,01117	0,0746	0,06850
5,070	377,55	0,02775		0,02855	0,0365	0,03630
2,030	410,95	0,00924		0,00863	0,1840	0,18700
5,070	410,95	0,02310		0,02400	0,0880	0,09100
2,030	444,15	0,00602		0,00577	0,4140	0,42600
5,070	444,15	0,01947		0,02017	0,1885	0,20250

108

1 / 141 2 3 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в папке Технология переработки природного газа и конденсата

#
02.03.201658.29 Кб641_Vved.pdf
#
02.03.20161.46 Mб642.pdf
#
02.03.20163.61 Mб643.pdf
#
02.03.20163.95 Mб624.pdf
#
02.03.2016295.36 Кб65Obtitul.pdf
#
02.03.201665.69 Кб62Oglav.pdf
#
02.03.2016171.74 Кб61SpisokLit.pdf

Ω3	− (2 − 3ζ )Ω2	+ 3ζ2	− ζ3 = 0.		(3.41)
b	c b	c	c
	àÁ Û ‡‚ÌÂÌËﬂ	(3.38) ÒÎÂ‰ÛÂÚ, ˜ÚÓ Ô‡ ‡ÏÂÚ ζc			ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ
НУ˝ЩЩЛˆЛВМЪЫ ТКЛП‡ВПУТЪЛ ‚ Н ЛЪЛ˜ВТНУИ ЪУ˜НВ (zÍ ). é‰Ì‡ÍÓ
‚ ‰‡ÌÌÓÏ ÒÎÛ˜‡Â ζc ﬂ‚ОﬂВЪТﬂ ЛПФЛ Л˜ВТНЛП Ф‡ ‡ПВЪ УП, УЪОЛ˜-
М˚П УЪ ЛТЪЛММУ„У zÍ ‚Â˘ÂÒÚ‚‡.
	З Ы ‡‚МВМЛЛ	ëÓ‡‚‡ ‚ÂÎË˜ËÌ‡ ζc ‰Îﬂ ‚ÒÂı ‚Â˘ÂÒÚ‚ Ô ËÌﬂÚ‡
‡‚ÌÓÈ 0,3333, ‡		‚ Ы ‡‚МВМЛЛ иВМ„‡ – кУ·ЛМТУМ‡ ζc= 0,3074.
ÖÒÎË ‚ Û ‡‚ÌÂÌËﬂ (3.39), (3.40), (3.41) ÔÓ‰ÒÚ‡‚ËÚ¸ ζc = 0,3333,
ÚÓ Ô‡ ‡ÏÂÚ c ·Û‰ÂÚ			‡‚ÂÌ ÌÛÎ˛,	Л Ы ‡‚МВМЛВ	(3.31) Ô Ë‚Ó-
‰ËÚÒﬂ Í Û ‡‚ÌÂÌË˛ ëÓ‡‚‡, ÂÒÎË ζc = 0,3074, ÚÓ Ò					= b Ë Û ‡‚ÌÂ-
МЛВ (3.31) Ф Л‚У‰ЛЪТﬂ Н Ы ‡‚МВМЛ˛ иВМ„‡ – кУ·ЛМТУМ‡.
	З Ы ‡‚МВМЛЛ и‡ЪВО – нВﬂ ‚ВОЛ˜ЛМ˚ ζc ‰Îﬂ ‡ÁÌ˚ı ‚Â˘ÂÒÚ‚
‡БМ˚В Л УФ В‰ВОﬂ˛ЪТﬂ ТУ‚ПВТЪМУ Т ‚ВОЛ˜ЛМ‡ПЛ					Ô‡ ‡ÏÂÚ ‡ F
ФУ ˝НТФВ ЛПВМЪ‡О¸М˚П БМ‡˜ВМЛﬂП				ФОУЪМУТЪЛ Л	‰‡‚ÎÂÌËﬂ	Ì‡-
Ò˚˘ÂÌÌÓ„Ó Ô‡ ‡ ˜ËÒÚ˚ı ‚Â˘ÂÒÚ‚.
	СОﬂ МВФУОﬂ М˚ı ‚В˘ВТЪ‚ ˝ЪЛ			Ô‡ ‡ÏÂÚ ˚ ÏÓ„ÛÚ ·˚Ú¸		‡Ò-
Т˜ЛЪ‡М˚ ЛБ ТОВ‰Ы˛˘Лı Ы ‡‚МВМЛИ:
F = 0,452413 + 1,30982ω – 0,295937ω2;					(3.42)
ζc = 0,329032 – 0,076799ω – 0,0211947ω2,					(3.43)
„‰В ω – Щ‡НЪУ ‡ˆВМЪ Л˜МУТЪЛ.
	СОﬂ ТПВТВИ Ф‡ ‡ПВЪ ˚ Ы ‡‚МВМЛﬂ и‡ЪВО – нВﬂ ‚˚˜ЛТОﬂ˛Ъ-

Ω3	− (2 − 3ζ )Ω2	+ 3ζ2	− ζ3 = 0.		(3.41)
b	c b	c	c
	àÁ Û ‡‚ÌÂÌËﬂ	(3.38) ÒÎÂ‰ÛÂÚ, ˜ÚÓ Ô‡ ‡ÏÂÚ ζc			ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ
НУ˝ЩЩЛˆЛВМЪЫ ТКЛП‡ВПУТЪЛ ‚ Н ЛЪЛ˜ВТНУИ ЪУ˜НВ (zÍ ). é‰Ì‡ÍÓ
‚ ‰‡ÌÌÓÏ ÒÎÛ˜‡Â ζc ﬂ‚ОﬂВЪТﬂ ЛПФЛ Л˜ВТНЛП Ф‡ ‡ПВЪ УП, УЪОЛ˜-
М˚П УЪ ЛТЪЛММУ„У zÍ ‚Â˘ÂÒÚ‚‡.
	З Ы ‡‚МВМЛЛ	ëÓ‡‚‡ ‚ÂÎË˜ËÌ‡ ζc ‰Îﬂ ‚ÒÂı ‚Â˘ÂÒÚ‚ Ô ËÌﬂÚ‡
‡‚ÌÓÈ 0,3333, ‡		‚ Ы ‡‚МВМЛЛ иВМ„‡ – кУ·ЛМТУМ‡ ζc= 0,3074.
ÖÒÎË ‚ Û ‡‚ÌÂÌËﬂ (3.39), (3.40), (3.41) ÔÓ‰ÒÚ‡‚ËÚ¸ ζc = 0,3333,
ÚÓ Ô‡ ‡ÏÂÚ c ·Û‰ÂÚ			‡‚ÂÌ ÌÛÎ˛,	Л Ы ‡‚МВМЛВ	(3.31) Ô Ë‚Ó-
‰ËÚÒﬂ Í Û ‡‚ÌÂÌË˛ ëÓ‡‚‡, ÂÒÎË ζc = 0,3074, ÚÓ Ò					= b Ë Û ‡‚ÌÂ-
МЛВ (3.31) Ф Л‚У‰ЛЪТﬂ Н Ы ‡‚МВМЛ˛ иВМ„‡ – кУ·ЛМТУМ‡.
	З Ы ‡‚МВМЛЛ и‡ЪВО – нВﬂ ‚ВОЛ˜ЛМ˚ ζc ‰Îﬂ ‡ÁÌ˚ı ‚Â˘ÂÒÚ‚
‡БМ˚В Л УФ В‰ВОﬂ˛ЪТﬂ ТУ‚ПВТЪМУ Т ‚ВОЛ˜ЛМ‡ПЛ					Ô‡ ‡ÏÂÚ ‡ F
ФУ ˝НТФВ ЛПВМЪ‡О¸М˚П БМ‡˜ВМЛﬂП				ФОУЪМУТЪЛ Л	‰‡‚ÎÂÌËﬂ	Ì‡-
Ò˚˘ÂÌÌÓ„Ó Ô‡ ‡ ˜ËÒÚ˚ı ‚Â˘ÂÒÚ‚.
	СОﬂ МВФУОﬂ М˚ı ‚В˘ВТЪ‚ ˝ЪЛ			Ô‡ ‡ÏÂÚ ˚ ÏÓ„ÛÚ ·˚Ú¸		‡Ò-
Т˜ЛЪ‡М˚ ЛБ ТОВ‰Ы˛˘Лı Ы ‡‚МВМЛИ:
F = 0,452413 + 1,30982ω – 0,295937ω2;					(3.42)
ζc = 0,329032 – 0,076799ω – 0,0211947ω2,					(3.43)
„‰В ω – Щ‡НЪУ ‡ˆВМЪ Л˜МУТЪЛ.
	СОﬂ ТПВТВИ Ф‡ ‡ПВЪ ˚ Ы ‡‚МВМЛﬂ и‡ЪВО – нВﬂ ‚˚˜ЛТОﬂ˛Ъ-

Ω3	− (2 − 3ζ )Ω2	+ 3ζ2	− ζ3 = 0.		(3.41)
b	c b	c	c
	àÁ Û ‡‚ÌÂÌËﬂ	(3.38) ÒÎÂ‰ÛÂÚ, ˜ÚÓ Ô‡ ‡ÏÂÚ ζc			ÒÓÓÚ‚ÂÚÒÚ‚ÛÂÚ
НУ˝ЩЩЛˆЛВМЪЫ ТКЛП‡ВПУТЪЛ ‚ Н ЛЪЛ˜ВТНУИ ЪУ˜НВ (zÍ ). é‰Ì‡ÍÓ
‚ ‰‡ÌÌÓÏ ÒÎÛ˜‡Â ζc ﬂ‚ОﬂВЪТﬂ ЛПФЛ Л˜ВТНЛП Ф‡ ‡ПВЪ УП, УЪОЛ˜-
М˚П УЪ ЛТЪЛММУ„У zÍ ‚Â˘ÂÒÚ‚‡.
	З Ы ‡‚МВМЛЛ	ëÓ‡‚‡ ‚ÂÎË˜ËÌ‡ ζc ‰Îﬂ ‚ÒÂı ‚Â˘ÂÒÚ‚ Ô ËÌﬂÚ‡
‡‚ÌÓÈ 0,3333, ‡		‚ Ы ‡‚МВМЛЛ иВМ„‡ – кУ·ЛМТУМ‡ ζc= 0,3074.
ÖÒÎË ‚ Û ‡‚ÌÂÌËﬂ (3.39), (3.40), (3.41) ÔÓ‰ÒÚ‡‚ËÚ¸ ζc = 0,3333,
ÚÓ Ô‡ ‡ÏÂÚ c ·Û‰ÂÚ			‡‚ÂÌ ÌÛÎ˛,	Л Ы ‡‚МВМЛВ	(3.31) Ô Ë‚Ó-
‰ËÚÒﬂ Í Û ‡‚ÌÂÌË˛ ëÓ‡‚‡, ÂÒÎË ζc = 0,3074, ÚÓ Ò					= b Ë Û ‡‚ÌÂ-
МЛВ (3.31) Ф Л‚У‰ЛЪТﬂ Н Ы ‡‚МВМЛ˛ иВМ„‡ – кУ·ЛМТУМ‡.
	З Ы ‡‚МВМЛЛ и‡ЪВО – нВﬂ ‚ВОЛ˜ЛМ˚ ζc ‰Îﬂ ‡ÁÌ˚ı ‚Â˘ÂÒÚ‚
‡БМ˚В Л УФ В‰ВОﬂ˛ЪТﬂ ТУ‚ПВТЪМУ Т ‚ВОЛ˜ЛМ‡ПЛ					Ô‡ ‡ÏÂÚ ‡ F
ФУ ˝НТФВ ЛПВМЪ‡О¸М˚П БМ‡˜ВМЛﬂП				ФОУЪМУТЪЛ Л	‰‡‚ÎÂÌËﬂ	Ì‡-
Ò˚˘ÂÌÌÓ„Ó Ô‡ ‡ ˜ËÒÚ˚ı ‚Â˘ÂÒÚ‚.
	СОﬂ МВФУОﬂ М˚ı ‚В˘ВТЪ‚ ˝ЪЛ			Ô‡ ‡ÏÂÚ ˚ ÏÓ„ÛÚ ·˚Ú¸		‡Ò-
Т˜ЛЪ‡М˚ ЛБ ТОВ‰Ы˛˘Лı Ы ‡‚МВМЛИ:
F = 0,452413 + 1,30982ω – 0,295937ω2;					(3.42)
ζc = 0,329032 – 0,076799ω – 0,0211947ω2,					(3.43)
„‰В ω – Щ‡НЪУ ‡ˆВМЪ Л˜МУТЪЛ.
	СОﬂ ТПВТВИ Ф‡ ‡ПВЪ ˚ Ы ‡‚МВМЛﬂ и‡ЪВО – нВﬂ ‚˚˜ЛТОﬂ˛Ъ-