Gidravlika_i_podzemnaya_gidromekhannika / poz066 buklet

в) результат расчета значений функций хn , n x и lgx некоторого приближенного числа х должен содержать столько значащих цифр, столько их имеется в числе х.

При вычислении промежуточных результатов сохраняют на одну цифру больше, чем рекомендуют правила а) - в) (так называемая запасная цифра). В окончательном результате запасная цифра отбрасывается.

Если некоторые приближенные числа содержат больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня и т.д.), чем другие, то их предварительно округляют, сохраняя только одну лишнюю цифру.

Пример 1. Перед сложением приближенных чисел 0,374; 13,1 и 2,065 первое и третье из них нужно округлить до сотых, а в окончательном результате сотые отбросить:

две значащие цифр (по количеству значащих цифр в числе 7,2):

Пример 3. Результат перемножения чисел 13,27 и 0,84 можно записать с тремя значащими цифрами (см. исключение из правила б)):

13,27 0,84 ≈13,3 0,84 ≈11,2 (а не 11).

Пример 4. При возведении в куб приближенного числа 216 результат должен быть записан только с тремя значащими цифрами:

2163 ≈101 105 .

Примечание. «Правила работы с приближенными числами» были приняты из справочника по физике [1].

16

Федеральное агентство по образованию Государственноеобразовательноеучреждениевысшегопрофессиональногообразования

Ухтинский государственный технический университет (УГТУ)

Изучение физических свойств жидкости

Методические указания

Ухта 2010

УДК 532 (076.5) И 85

Исакова, А. А.

Изучение физических свойств жидкости [Текст] : метод. указания / А. А. Исакова. – Ухта : УГТУ, 2010. – 16 с.

Методические указания предназначены для лабораторных занятий по гидравлике. Методические указания могут быть использованы для всех специальностей, изучающих дисциплину «Гидравлика». В них приведены теоретические сведения, порядок выполнения лабораторной работы, расчетные формулы и обработка опытных данных.

Методические указания рассмотрены и одобрены заседанием кафедры Разработка и эксплуатация нефтяных и газовых месторождений и подземной гидромеханики от 24.06.2010 г. пр. № 6.

Рецензент: Рочев А. Н., доцент кафедры разработка и эксплуатация нефтяных и газовых месторождений и подземной гидромеханики Ухтинского государственного технического университета, к.т.н.

Редактор: Корохонько О. М., старший преподаватель кафедры разработка и эксплуатация нефтяных и газовых месторождений и подземной гидромеханики Ухтинского государственного университета.

В лабораторных указаниях учтены предложения рецензента и редактора.

План 2010 г., позиция 66.

Подписано в печать 30.06.2010 г. Компьютерный набор. Объем 16 с. Тираж 100 экз. Заказ № 243.

©Ухтинский государственный технический университет, 2010 169300, Республика Коми, г. Ухта, ул. Первомайская, д. 13. Отдел оперативной полиграфии УГТУ.

169300, Республика Коми, г. Ухта, ул. Октябрьская, д. 13.

ПРИЛОЖЕНИЕ Б

Правила работы с приближенными числами

Производя обработку многочисленных измерений, часто не подсчитывают погрешности отдельных результатов и судят о погрешности приближенного значения величины (числа), указывая количество верных значащих цифр в этом числе.

1. Нули, стоящие в числе слева, значащими цифрами не считаются. Нули в середине или в конце числа (справа), обозначающие отсутствие в числе единиц соответствующих разрядов, - значащие цифры. Например, в числе 0,08040 первые два нуля – не значащие, а третий и четвертый – значащие.

Нули, поставленные в конце целого числа взамен неизвестных цифр и служащие лишь для определения разрядов остальных цифр, значащими не считаются. В подобных случаях нули в конце числа лучше не писать и заменять их соответствующей степенью числа 10. Например, если число 4200 измерено с абсолютной погрешностью ±100, то это число должно быть записано в виде 4,2 103 . Такая запись подчеркивает, что в данном числе содержатся лишь две значащие цифры.

2. Если приближенное значение величины содержит лишние или недостоверные цифры, то его округляют, сохраняя только верные значащие цифры и отбрасывая лишние. При этом руководствуются следующими правилами округления:

а) если первая отбрасываемая цифра больше 4, то последняя сохраняемая цифра увеличивается на единицу. Например, округляя число 27,3763 до сотых, следует записать 27,38;

б) если первая отбрасываемая цифра меньше 4 или равна 4, то последняя сохраняемая цифра не изменяется. Например, округляя число 13847 до сотен, записы-

вают 138 102 ;

в) если отбрасываемая часть числа состоит из одной цифры 5, то число округляют так, чтобы последняя сохраняемая цифра была четной. Например при округле-

нии до десятых 23,65 ≈23,6, но 17,75 ≈17,8.

3. Производя различные математические действия с приближенными числами, руководствуются следующими правилами подсчета цифр:

а) при сложении и вычитании в результате сохраняют столько десятичных знаков, сколько содержится в числе с наименьшим количеством десятичных знаков;

б) при умножении и делении в результате сохраняют столько значащих цифр, сколько их имеет приближенное число с наименьшим количеством значащих цифр.

Исключение из этого правила допускается в тех случаях, когда один из сомножителей произведения начинается с единицы, а сомножитель, содержащий наименьшее количество значащих цифр, - с какой-нибудь другой цифры. В этих случаях в результате сохраняют на одну цифру больше, чем в числе с наименьшим количеством значащих цифр;

15

ВВЕДЕНИЕ

Комплекс лабораторных опытов, представленных в данных методических указаниях, направлен на определение физических свойств жидкости. Целью предлагаемых методических указаний является помощь студентам в технике проведения экспериментальных исследований. Для проведения каждого опыта предложен порядок выполнения работы, приведены расчетные формулы и обработка опытных данных.

Наблюдения, измерения и вычисления при выполнении лабораторной работы осуществляются студентами самостоятельно. Преподаватель контролирует проведение опыта, обработку материалов и принимает выполненную работу.

Сдавая работы, студент должен дать качественную оценку полученных результатов.

1. ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ

Жидкими телами, или жидкостями, называют физические тела, легко изменяющие свою форму под действием самых незначительных сил. В отличие от твердых тел жидкости характеризуются весьма большой подвижностью своих частиц и поэтому обладают свойством текучести и способностью принимать форму сосуда, в который они налиты.

Различают жидкости капельные и газообразные. Капельные – это жидкости, встречающиеся в природе и применяемые в технике: вода, нефть, бензин и т.д. Все капельные жидкости оказывают большое сопротивление изменению объема и трудно поддаются сжатию. При изменении давления и температуры их объем изменяется весьма незначительно. Газообразные жидкости (газы) изменяют свой объем под влиянием указанных факторов в значительной степени.

Состояние и поведение встречающихся в природе и применяемых в технике жидкостей находятся в непосредственной зависимости от их физических свойств. Поэтому первая задача, предшествующая изучению гидравлики, − определение физических свойств жидкостей, выявление факторов, влияющих на них, и установление единиц их измерения.

Плотностью называют количество массы (m) жидкости, содержащееся в единице объема (V), ее обозначают греческой буквой ρ и определяют из отношения:

ρ = Vm .

Единицей плотности является килограмм на кубический метр (кг/м3).

4

3 ЗАЩИТА ЛАБОРАТОРНОЙ РАБОТЫ

Для защиты лабораторной работы необходимо предоставить отчет по лабораторной работе (см. пункт 2.5) и ответить на следующие контрольные вопросы:

1). Что называется плотностью жидкости? Единица измерения плотности. Какой прибор служит для измерения плотности? Принцип работы.

2). Что называется вязкостью жидкости? Коэффициенты динамической и кинематической вязкости. Единицы измерения. Какие приборы служит для измерения вязкости? Их принцип работы.

3). Что называется поверхностным натяжением? Единицы измерения коэффициента поверхностного натяжения. Какой прибор служит для определения поверхностного натяжения? Принцип работы.

4). Что характеризует коэффициент сжимаемости, коэффициент теплового расширения? Единицы измерения.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Справочник по физике [Текст] / Б. М Яворский – М., Наука. Главная редакция физико-математической литературы, 1985. – 512 с.

2.Слабожанин, Г. Д. Практикум по гидравлике на портативной лаборатории «Капелька» [Текст]: метод. указания к лабораторным работам / Г. Д. Слабожанин – Томск. : Архитектурно-строительныйуниверситет, 2007. – 28 с.

3. Рабинович, Е. З. Гидравлика [Текст]: учеб. пособие для вузов / Е. З. Рабинович. – М.: Недра., 1980. – 278 с.

13

ренным на конце для накопления жидкости в виде капли. Сила поверхностного натяжения в момент отрыва капли равна ее весу (силе тяжести) и поэтому определяется по плотности жидкости и числу капель, полученному при опорожнении емкости с заданным объемом.

Для выполнения опыта № 4 выполнить следующие действия:

1) перевернуть устройство «Капелька» и подсчитать число капель, полученных в сталагмометре 5 из объема высотой S между двумя метками. Опыт повторить три раза и вычислить среднеарифметическое значение числа капель n;

2) найти опытное значение коэффициента поверхностного натяжения по формуле:

σ = К ρТ* ,

nср

где К – постоянная сталагмометра, м3/с3; ρT* – плотность жидкости по справочным данным при температуре опыта Т, кг/м3;

3)полученный результат σ сравнить с табличным значением σ*20 (см. таблицу 1.3) и сделать соответствующие выводы;

4)значения исходных данных и результаты расчетов внести в таблицу 2.4.

Таблица 2.4 – Опыт № 4

Примечание. В таблице 1.3 приведены значения плотности ρ, вязкости ν и поверхностного натяжения σ жидкостей при температуре 20 0С. Поэтому опытные значения, полученные при другой температуре, могут существенно отличаться от табличных значений.

2.5 Оформление отчета по лабораторной работе

Отчет должен содержать:

1)титульный лист (приложение А);

2)цель лабораторной работы;

3)схему установки (см. рисунок 2.1);

4)основные расчетные формулы для каждого опыта;

5)полученные результаты расчетов обработать в соответствии с приложением Б и внести в таблицы 2.1, 2.2, 2.3, 2.4.

12

Плотности обычных капельных жидкостей (за исключением ртути) близки к плотности воды (таблица 1.1) и весьма слабо изменяются с изменением температуры

идавления.

Сповышением температуры плотность жидкостей, как правило, уменьшается. Некоторым исключением из этого общего правила является вода при температуре от 0 до 40С. В этом интервале температур наибольшую плотность вода имеет при 40С (таблица 1.2).

Вязкость свойство жидкости сопротивляться относительному скольжению ее слоев. Это свойство не может быть обнаружено при покое жидкости, так как оно проявляется лишь при ее движении.

При движении различные слои жидкости или газа перемещаются с разной скоростью, что вызывает молекулярный обмен на условной поверхности раздела слоев. Это порождает силы, тормозящие движение одного слоя и ускоряющие другой. Количественно вязкость характеризуется коэффициентом динамической вязкости µ.

Таблица 1.1 – Плотность некоторых жидкостей

Таблица 1.2 – Плотность воды при атмосферном давлении

Размерность коэффициента динамической вязкости в международной системе единиц СИ − Па с. В гидравлике используют также коэффициент кинематической вязкости ν, который равен отношению коэффициента динамической вязкости к плотности вещества:

5

где G – сила тяжести, Н; F – сила сопротивления, Н; Fарх – выталкивающая (архимедова) сила, Н.

Распишем, чему равна сила тяжести:

где Rш – радиус шарика, м; ρш – плотность шарика, кг/м3; g – ускорение свободного падения, м/с2.

где Сх – безразмерный коэффициент сопротивления; ω – площадь проекции шарика на плоскость, нормальную к направлению движения, м2; υ – скорость жидкости относительно шарика (или, что тоже самое, шарика относительно жидкости), м/с.

Подставим формулы (1.3), (1.4), (1.5) в формулу (1.1), получим:

6

3)сравнить опытное значение коэффициента кинематической вязкости ν с табличным значением ν*20 (см. таблицу 1.3) и сделать соответствующие выводы;

4)значения исходных данных и результаты расчетов внести в таблицу 2.2.

Таблица 2.2 – Опыт № 2

2.3 Опыт № 3 «Определение вязкости капиллярным вискозиметром»

Капиллярный вискозиметр 4 (см. рисунок 2.1) включает емкость с капилляром. Вязкость определяется по времени истечения жидкости из емкости через капилляр.

Необходимо выполнить следующие действия:

1)перевернуть устройство «Капелька» (см. рисунок 2.1) в вертикальной плоскости и определить секундомером время t истечения через капилляр объема жидкости между двумя метками (высотой S) из емкости вискозиметра 4, опыт выполнить три раза, а затем определить среднеарифмeтическое значение времени t;

2)определить температуру Т по термометру 1;

3)вычислить значение кинематического коэффициента вязкости ν по следующей формуле:

ν = M tср ,

где М – постоянная прибора, м2/с2;

4)сравнить опытное значение коэффициента кинематической вязкости ν с табличным значением ν*20 (см. таблицу 1.3) и сделать соответствующие выводы;

5)значения исходных данных и результаты расчетов внести в таблицу 2.3.

Таблица 2.3 – Опыт № 3

2.4 Опыт № 4 «Определение поверхностного натяжения сталагмометром»

Сталагмометр 5 (см. рисунок 2.1) служит для определения поверхностного натяжения жидкости методом отрыва капель и содержит емкость с капилляром, расши-

11

3)сравнить опытное значение плотности ρ со значением плотности ρT* , вычисленным по справочным данным и сделать соответствующие выводы:

где ρT* – плотность жидкости по справочным данным при температуре опыта Т, кг/м3;

ρ*20 – плотность жидкости при температуре 200С (справочное значение см. таблицу 1.3); βТ – коэффициент температурного расширения (в среднем для минеральных масел и нефти можно принять βТ = 0,0007 1/0С; для воды, бензина, керосина

βТ = 0,0003 1/0С); 4) значения исходных данных и результаты расчетов внести в таблицу 2.1.

Таблица 2.1 – Опыт № 1

2.2 Опыт № 2 «Определение вязкости вискозиметром Стокса»

Вискозиметр Стокса 3 достаточно прост (см. рисунок 2.1), содержит цилиндрическую емкость, заполненную исследуемой жидкостью, и шарик. Прибор позволяет определить вязкость жидкости по времени падения шарика в ней следующим образом:

1)повернуть устройство «Капелька» в вертикальной плоскости на 1800 и зафиксировать секундомером время t прохождения расстояния l между двумя метками в приборе 3. Шарик должен падать по оси емкости без соприкосновения со стенками. Опыт выполнить три раза, а затем определить среднеарифмeтическое значение времени t;

2)вычислить опытное значение кинематического коэффициента вязкости жидкости согласно формуле (1.13):

где g – ускорение свободного падения, м2/с; dш, D – диаметры шарика и цилиндрической емкости, м; ρш – плотность жидкости и материала шарика, кг/м3; ρT* – плотность жидкости по справочным данным при температуре опыта Т, кг/м3, вычисляется по формуле (2.2);

10

Поверхностное натяжение – свойство жидкости образовывать поверхностный слой взаимно притягивающих молекул – характеризуется коэффициентом поверхностного натяжения σ, равным силе на единицу длины контура свободной поверхности. Значения вязкости ν и поверхностного натяжения σ при 200С приведены в таблице 1.3.

Таблица 1.3 – Значение плотности ρ, вязкости ν и поверхностного натяжения σ жидкостей при 200С

Сжимаемость – свойство жидкости уменьшать свой объем под действием дав-

ления. Она оценивается коэффициентом (объемного сжатия) сжимаемости βр, по-

казывающим относительное уменьшение объема W при повышении давления Р на единицу:

βP = − ∆W / ∆P .

W

Тепловое (температурное) расширение – свойство жидкости изменять свой объем при нагревании. Оно характеризуется коэффициентом теплового расширения βТ, равным относительному приращению объема W с изменением температуры Т на один градус при постоянном давлении:

βT = ∆WW / ∆T .

Как правило, при нагревании объем жидкости увеличивается.

2 ПРОВЕДЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ

Цель работы: освоение техники измерения плотности, вязкости и поверхностного натяжения жидкости.

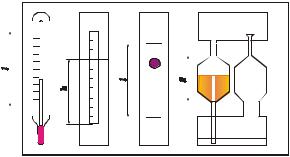
Лабораторная работа проводится на устройстве «Капелька». Устройство для изучения физических свойств жидкости содержит 5 приборов, выполненных в общем прозрачном корпусе (рисунок 2.1), на котором указаны параметры для обработки опытных данных. Приборы 3÷5 начинают действовать при перевертывании устройст-

8

ва «Капелька». Термометр 1 показывает температуру окружающей среды и, следовательно, температуру жидкостей во всех устройствах.

Рисунок 2.1 − Схема устройства «Капелька»

1– термометр; 2 – ареометр; 3 – вискозиметр Стокса; 4 – капиллярный вискозиметр; 5 – сталагмометр

2.1Опыт № 1 «Определение плотности жидкости ареометром»

Плотность жидкости определяют различными способами. В производственных условиях плотность обычно измеряют специальным прибором, называемым ареометром (см. рисунок 2.1). Ареометр 2 служит для определения плотности жидкости поплавковым методом. Он представляет собой пустотелый цилиндр с миллиметровой шкалой и грузом в нижней части. Благодаря грузу ареометр плавает в исследуемой жидкости в вертикальном положении. Глубина погружения ареометра является мерой плотности жидкости и считывается со шкалы по верхнему краю мениска жидкости вокруг ареометра. В обычных ареометрах шкала отградуирована сразу по плотности.

Входе работы необходимо выполнить следующие операции:

1)измерить глубину погружения h ареометра по миллиметровой шкале на нем;

2)вычислить плотность жидкости по следующей формуле:

G = m g и выталкивающей (архимедовой) силы Pарх = ρ g W , где объем погру-