5. Примеры решения задач

Задача 1. Найти потери напора по длине при движении воды с температурой t= 50°С в цельносварной стальной трубе, бывшей в употреблении, с внутренним диаметромd= 0,5 м. Расход водыQ=0,60 м³/с. Длина трубы 1=500 м.

Решение.

Находим по таблице [1] значение абсолютной эквивалентной шероховатости трубы k_э= 0,15 мм = 15 10^-5м;k_э/d= 15 10^-5/0,5 = 0,0003. Кинематический коэффициент вязкости для воды заданной температуры ν = 0,00556 см²/с.

Средняя скорость течения воды в трубе

Число Рейнольдса для потока воды в трубе

Режим движения турбулентный, поэтому коэффициента гидравлического трения находится по формуле (1)

Потери напора по длине

столба воды приt= 50°С.

Плотность воды находим из табл. 1 ρ =988,07 кг/м3.

Потери полного давления по длине Δp_тр= ρgh_тр= 988,07ּ9,81ּ7,15 =  = 69,4ּ10³Н/м²=69,4 кПа.

Задача 2. Найти потери напора по длине на один метр длинны при движении воздуха в бетонной трубе диаметром d=lм при давлении, близком к атмосферному, и температуреt= 20° С. Расход воздуха при заданных условияхQ= 15,6 м³/с

Решение

Заданному состоянию воздуха соответствует кинематический коэффициент вязкости ν= 15,7 10^-6м²/с и плотностьρ= 1,16 кг/м³

Находим число Рейнольдса, характеризующее поток воздуха в трубе

Определим относительную шероховатость трубопровода (при абсолютной эквивалентной шероховатости k_э= 0,5 мм):

Находим величину коэффициента гидравлического трения по обобщенной формуле

Определяем потерю полного давления на 1 пот. м трубы:

Задача 3. Определить величину потерь полного давления, вызванных резким поворотом трубопровода диаметром d= 200 мм на угол а = 90°. Трубопровод новый стальной, радиус поворотаR= 40 м. Жидкость - масло минеральное ν = 14,5 10^-4м²/с. ρ = 880 кг/м³. Расход жидкостиQ= 0,5 м³/с.

Решение.

Потери полного давления в повороте находим по формуле Δр = ξ ρ υ²/2.

Коэффициент сопротивления поворота находим по формуле (5)

где ξ_кв- коэффициент сопротивления поворота ξ_кв= 1. Число Рейнольдса

Из таблиц [1] коэффициент А =400,

Задача 4. Определить расход минерального масла (плотностью ρ = 880 кг/м^3,кинематической вязкостьюv= 10 10^-4м²/с) при истечении в атмосферу через круглое отверстие диаметромd=2 см из резервуара, в котором давление (избыточное) р =5 10⁵Н/м².

Решение.

Определяем число Рейнольдса, характеризующее истечение,

Из графика находим величину коэффициента расхода μ = 0,69. Определяем расход масла

Задача 5. В дне сосуда имеется отверстие с закругленной кромкой d= 3 мм. Высота уровня воды в сосудеH=0,05 м. Определить скорость и расход при вытекании холодной (t₁= 6°C) и горячей (t₂= 99°С) воды из отверстия.

Решение.

Скорость вытекания воды из отверстия находим по формуле

Коэффициент скорости φ находим из графика в функции от числа Рейнольдса, характеризующего истечение из отверстия.

Из таблиц [1] находим кинематический коэффициент вязкости воды.

ν₁= 1, 47 10-6 м²/с;ν₂= 0, 29 1^0-6 м²/с. Соответственно числа Рейнольдса будут равны

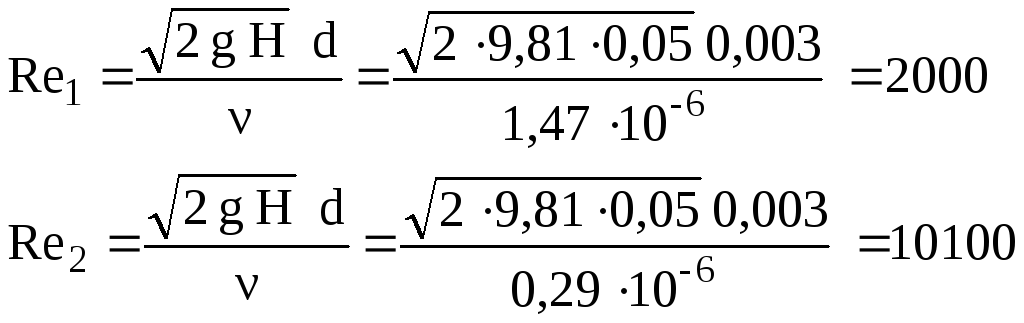
Из графика Альтшуля φ₁= 0,86,φ₂=0,94.

Скорость вытекания холодной воды v₁= 0,98φ=0,98 0,86=0,85 м/с.

Скорость вытекания горячей воды v2=0,98 0,94=0,92 м/с.

Таким образом, горячая вода имеет скорость вытекания больше чем холодная, на (0,92 - 0,85)/0,85 100% = 8%, Это объясняется большей подвижностью (меньшей вязкостью) горячей воды.