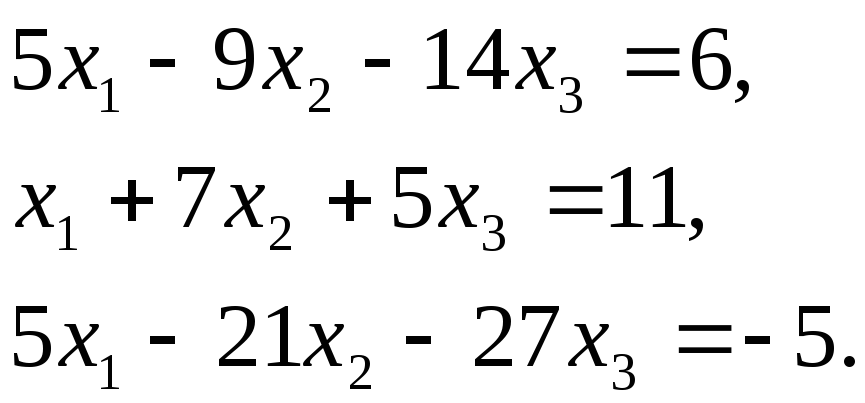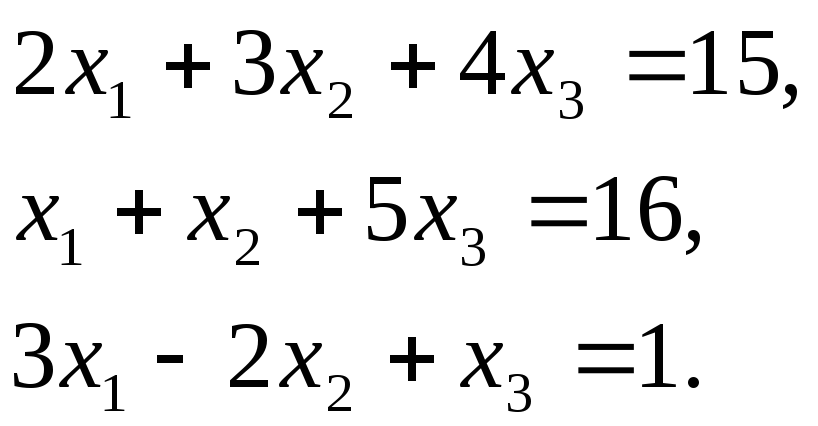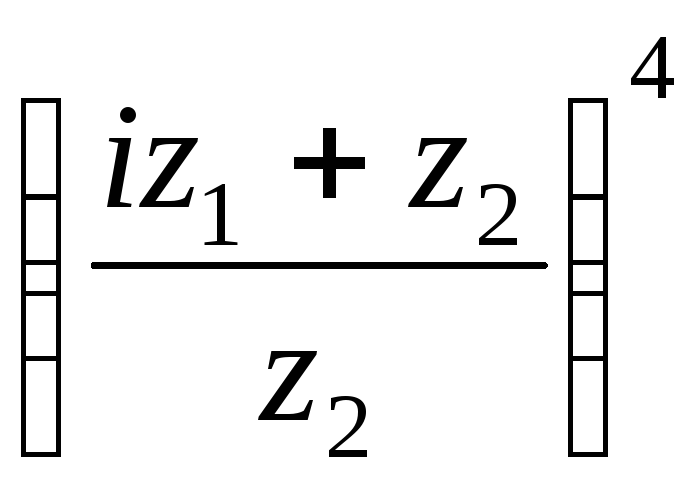1.5. Список литературы

1. Высшая математика для экономистов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. Н.Ш.Кремера. – М.::ЮНИТИ, 2000.

2. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.I / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высшая школа, 2001.

3. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.II / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высшая школа, 2001.

4. Исследование операций в экономике / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 2004.

5. Красс, М.С. Математика для экономистов / Красс М.С., Чупрынов Б.П. – СПб.: Питер, 2007.

2. Контрольная работа по теме «линейная алгебра»

Задание 1. Операции над матрицами

Даны матрицы А, В, С и число k. Вычислите А(kВ^Т) + С.

Замечание: В^Т – матрица, транспонированная матрице В.

№	А	В	С	k
1				3
2				2
3				4
4				2
5				3
6				-2
7				4
8				-3
9				3
10				-2

Задание 2. Системы линейных уравнений

Решите систему линейных уравнений:

а) по формулам Крамера, б) методом Гаусса, в) матричным методом.

№	Система уравнений	№	Система уравнений
11		16
№	Система уравнений	№	Система уравнений
12		17
13		18
14		19
15		20

Задание 3. Геометрия на плоскости

Даны координаты вершин треугольника АВС. Найдите:

а) длину стороны АВ;

б) угол А;

в) уравнение медианы СМ;

г) уравнение высоты СН;

д) площадь треугольника ABC.

№	А	В	С
21	(-8; 3)	(4; -12)	(8; 10)
22	(-5; 7)	(7; -2)	(11; 20)
23	(-12; -1)	(0; -10)	(4; 12)
24	(-10; 9)	(2; 0)	(6; 22)
25	(0; 2)	(12; -7)	(16; 15)
26	(-9; 6)	(3; -3)	(7; 19)
27	(1; 0)	(13; -9)	(17; 13)
28	(-4; 10)	(8; 1)	(12; 23)
29	(2; 5)	(14; -4)	(18; 18)
30	(-1; 4)	(11; -5)	(15; 17)

Задание 4. Прямая и плоскость в пространстве

Даны три плоскости: ₁, ₂, ₃ и прямая l в пространстве. Найдите:

а) точку пересечения плоскостей ₁, ₂, ₃,

б) нормаль к плоскости ₂,

в) направляющий вектор прямой l,

г) расстояние от точки М до плоскости ₁,

д) точку пересечения прямой l с плоскостью ₂,

е) прямую, проходящую через точку М, перпендикулярно плоскости ₃.

№	1	2	3	l	М
31	2х-3у+z=7	x-y-z=-1	5x-7y+5z=3	==	(1;-3;2)
32	x-y+z=-1	x=7	5x-2y+z=0	==	(1;-1;-1)
33	x +3y-2z=-12	-3x +5y+z=15	x-5y+2z=-1	==	(1;-2;3)
34	5x -4y-3z=-1	2x -3y+z=-1	4x -5y+2z=-7	==	(4;8;3)
35	5x -4y+z=2	3x +2y-3z=-2	4x +y=3	==	(-3;-2;5)
36	3x -5y+4z=-3	3x -5y-3z=-6	x -5y+z=1	==	(3;-1;-2)
37	x -2y+z=3	2x –y‑z=0	3x -2y+z=4	==	(-3;2;1)
38	9x -y+2z=0	4x -3y-5z=4	x -4z=3	==	(7;3;-1)
39	3x -2y+z=-12	5x +y-3z=15	2x -5y+z=0	==	(-2;1;3)
40	3x +2y-4z=-2	2x -2y+3z=4	4x -3y-2z=-1	==	(3;2;4)

Задание 5. Комплексные числа и действия над ними

Даны комплексные числа: z₁, z₂, z₃ . Найдите следующие выражения (а и б):

№	z 1	z 2	z 3	а)	б)
41
42
43
44
45
№	z 1	z 2	z 3	а)	б)
46
47
48
49
50

Задание 6. Математическая модель межотраслевого баланса (модель Леонтьева)

Имеются данные об исполнении баланса за отчетный период, усл. ден. ед.:

Отрасль	Потребление по отраслям			Конечный продукт	Валовый выпуск
	I	II	III
I	а11	а12	а13	у1	х1
II	а21	а22	а23	у2	х2
III	а31	а32	а33	у3	х3

Используя модель межотраслевого баланса (модель Леонтьева), вычислите необходимый объем валового выпуска каждой отрасли, если конечное потребление отрасли I увеличится вдвое, отрасли II – на 20%, а потребление по отрасли III останется на прежнем уровне.

№	а11	а12	а13	а21	а22	а23	а31	а32	а33	у1	у2	у3	х1	х2	х3
51	6	3	15	9	12	5	12	6	10	6	4	22	30	30	50
52	14	12	24	21	8	8	7	8	48	34	3	17	70	40	80
53	10	16	16	5	8	8	15	8	48	8	19	9	50	40	80
54	8	16	15	4	8	5	12	8	10	1	23	20	40	40	50
55	8	12	15	4	6	5	16	9	10	5	15	15	40	30	50
56	9	3	15	9	6	5	12	3	10	3	10	25	30	30	50
57	6	2	9	9	4	3	9	2	6	13	4	13	30	20	30
58	6	2	15	3	4	10	9	8	10	7	3	23	30	20	50
59	16	4	15	24	8	5	8	16	10	45	3	16	80	40	50
60	12	32	15	6	16	20	18	16	10	1	38	6	60	80	50