Лабораторна робота № 11

Визначення індуктивності котушки, ємності

Конденсатора та перевірка закону ома для

Електричного кола змінного струму

І. МЕТА РОБОТИ: вивчити особливості протікання змінного струму в електричних колах з різним характером навантаження; виміряти коефіцієнт самоіндукції L. ємність конденсатора С та перевірити закон Ома для електричного кола зі змішаним навантаженням R_a, L, C.

ІІ. ДЛЯ РОБОТИ ПОТРІБНІ: астатичний вольтметр типу АМВ з межами вимірювання 7,5; 15; 30; 60 В, астатичний вольтметр типу АСТВ з межами вимірювання 150 і 300 В, астатичний міліамперметр АСТ з межами вимірювання 250 і 500 мА, батарея конденсаторів типу БГ-МН ємністю 1 мкФ кожний, котушка індуктивності з L≈0,01 Гн, два реостати з опорами 200 і 400 Ом на 2 А.

Ііі. Теоретичні питання програми, знання яких необхідне для виконання роботи

1. Змінний струм та його одержання. Період і частота струму.

2. Амплітудне та ефективне значення змінного струму.

3. Активний і реактивний опір. Опір ємнісний та індуктивний.

4. Зсув фаз між струмом і напругою у конденсаторі та котушці самоіндукції.

5. Векторна діаграма кола змінного струму з послідовним з’єднанням R_a, L, C.

6. Закон Ома для змінного струму

IV. Теоретичні відомості та опис установки

1. Змінним називають електричний струм, напруга і сила якого періодично змінюються за величиною і напрямком.

Якщо до кінців провідника з активним опором R_a прикласти змінну напругу

, (11.1)

де - її амплітуда (максимальне значення),

- циклічна частота,

то в ньому виникає змінний електричний струм, сила якого в той же момент визначається за законом Ома:

, (11.2)

де - амплітуда струму.

2. Якщо ж крім опору R_a в коло буде включена також індуктивність з коефіцієнтом самоіндукції L, то під дією тієї ж напруги в колі виникає сила струму:

, (11.3)

де , (11.4)

а зсув фаз між струмом і напругою буде визначатися за формулою:

(11.5)

Співставлення формул (11.1) та (11.3) свідчить, що в цьому колі струм за фазою відстає від напруги на кут .

Величина

(11.4а)

носить назву опору даного кола, а величину

(11.4б)

називають індуктивним опором.

3. Якщо замість котушки самоіндукції в коло змінного струму включити конденсатор з ємністю С, то сила струму буде визначатися так:

, (11.6)

де амплітуда струму , (11.7)

а . (11.8)

Співставлення формул (11.1) та (11.6) свідчить, що в цьому колі струм за фазою випереджає напругу на кут .

Опір кола буде

, (11.7а)

причому . (11.7а)

називається ємнісним опором *.

4. Нарешті, якщо в коло включені послідовно всі три навантаження R_а, L і C, сила струму в колі може бути подана виразом:

,

де амплітуда струму:

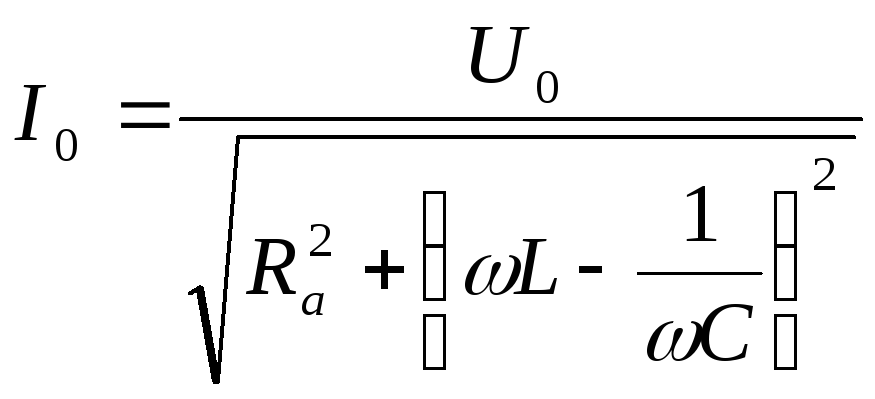, (11.8)

а . (11.8а)

Знаменник формули (11.8) дає повний опір кола змінному струмові.

Отже, формула (11.8) носить назву закону Ома для змінного струму.

В формули (11.2), (11.4), (11.6) і (11.8) входять І₀ та U₀ – амплітуди струму і напруги. Електричні ж прилади вимірюють ефективні їх значення І_еф та .

Можна показати, що

* Опір ємності постійному струмові R_C= ∞.

та . (11.10)

Тому вищевказані формули можуть бути записані і для ефективних значень струму та напруги:

, (11.11)

, (11.12)

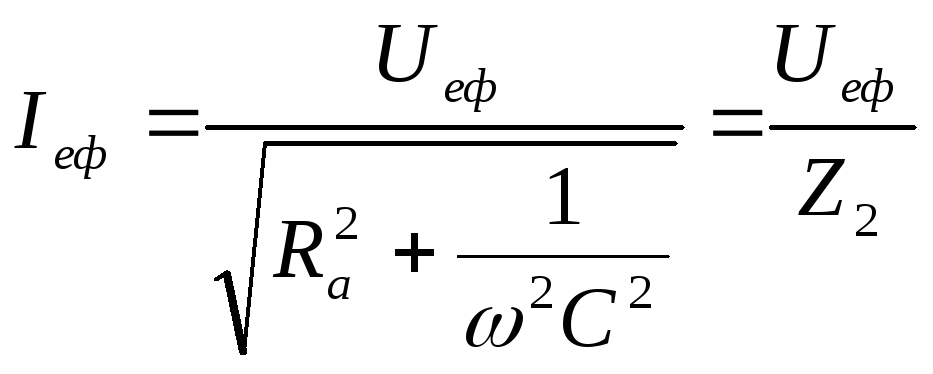, (11.13)

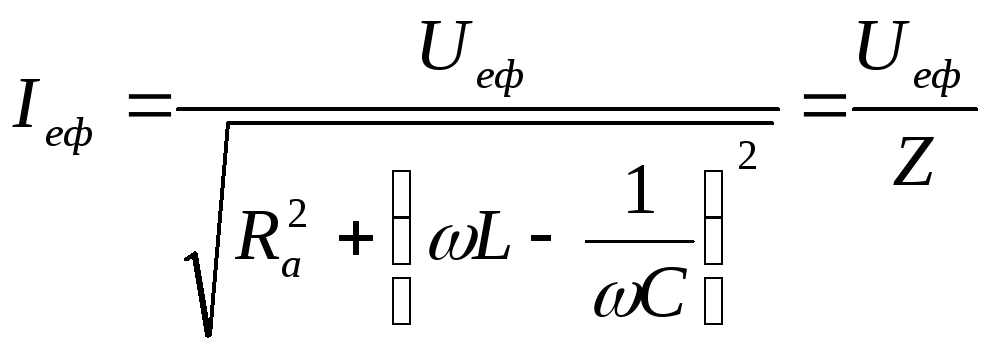. (11.14)

В усіх формулах (11.11) - (11.14) під R_а слід вважати суму всіх активних опорів електричного кола (включаючи й омічний опір котушки самоіндукції).