Эконометрика (лабораторные)

- ряд содержит сильную нелинейную тенденцию, для выявления которой необходимо провести дополнительный анализ.

Одним из наиболее простых и распространенных методов определения структуры временного ряда является построение графиков автокорреляционной (АКТ) и частной автокорреляционной (ЧАКТ) функций.

Автокорреляционная функция – это функция оценки коэффициента автокорреляции в зависимости от величины временного лага между исследуемыми рядами. Графиком АКФ является коррелограмма.

Задача 10.1. По данным таблицы динамики выпуска продукции некоторой страны за ряд лет

требуется:

а) провести расчет параметров линейного, логарифмического, полиномиального, степенного и экспоненциального трендов; б) построить графики рядов динамики и трендов;

в) выбрать наилучший вид тренда на основании их графического изображения и значений коэффициента (индекса) детерминации.

Решение.

Сохраним открытый файл под именем «лаб10.xls».

Внесем данные с подписями в диапазон А2:В38. В ячейке С2 внесем подпись t , в ячейках С3:С38 – значения 1,2,3,…,36. Для расчета

121

параметров линейного тренда снова воспользуемся функцией ЛИНЕЙН, выведя ее массив значений в диапазон Е2:F6 (в качестве известных значений t следует взять диапазон С3:С38). В ячейки D8:G8 выведем уравнение тренда yˆ 5969,522 977,11982t .

При анализе временных рядов широко применяются графические методы. Это объясняется тем, что табличное представление временного ряда и описательные характеристики не позволяют понять характер процесса, а по графику временного ряда можно сделать определенные выводы, которые могут быть проверены с помощью расчетов:

наличие тренда и его характеристик;

наличие сезонных и циклических компонент;

степени плавности и прерывистости изменений последовательных значений ряда после устранения тренда.

Для графического анализа временного ряда используем средство Мастер диаграмм. Выделите диапазон данных В3:В38, вызовите ВСТАВКА, Диаграммы выберите вид Точечная (см. лаб. Раб 3). В открывшемся диалоговом окне в поле Название диаграммы введите «Динамика выпуска продукции, усл. ед.», в поле Ось Х (категорий) – «Год, t», в поле Ось Y (значений) введите «Выпуск продукции, у».

Поскольку график рядов динамики будет тем же для других видов трендов, выделите диаграмму и скопируйте ее в буфер, затем вставьте из буфера 4 раза. Разместите диаграммы удобно, например, по две в ряд. Для того чтобы на 1-ой диаграмме получить линию линейного тренда, выполните действия: щелкните мышкой по области первой диаграммы, в правом верхнем углу выберите пункт «+», поставьте галочки в контекстных меню Легенда и Линия тренда. В окне Линия тренда нажать

Дополнительные параметры… и в появившемся окне ПАРАМЕТРЫ ЛИНИИ ТРЕНДА поставить точку в тип тренда Линейная, поставьте галочки рядом с пунктами Показывать уравнение на диаграмме, Поместить на диаграмму величину достоверности аппроксимации. На диаграмме появилась линия тренда, уравнение тренда и величина R 2 . Сравните коэффициенты уравнения и значение R 2 с результатами, полученными с использованием функции ЛИНЕЙН (в ячейках F2, E2, E4).

На всех остальных диаграммах добавьте линии тренда, выбирая разный тип линии: логарифмическая, полиномиальная (6-той степени), степенная и экспоненциальная. Везде выводите уравнение линии тренда и величину достоверности аппроксимации R 2 .

Сравним значения R 2 для разных видов трендов:

122

Как видно, исходные данные лучше всего описывает полином 6-ой степени. Это подтверждается и визуальным осмотром. Однако вид этой функции достаточно сложен. Возможно, более рационально в исследовательских целях (например, для расчета прогнозных значений) использовать экспоненциальную линию тренда, для которой значение R 2 незначительно меньше, однако ее вид более прост и удобен для интерпретации.

Задача 10.2. Имеются данные (усл. ед.) об объеме потребления электроэнергии y за четыре года (поквартально):

использованием фактора времени и фиктивных переменных.

Решение.

Введем фиктивные переменные:

123

Вфайле перейдем на «Лист2», внесем данную таблицу в ячейки А2:Е18. Для нахождения коэффициентов уравнения воспользуемся функцией ЛИНЕЙН. Выведем ее результаты в ячейки А21:Е25. Создадим шаблон для вывода уравнения:

Вячейках G21, H21, J21, L21, O21 выведите коэффициенты регрессии, полученные в результате использования функции ЛИНЕЙН.

Оцененное уравнение регрессии:

yˆ 6,2375 0,1875t 2,3875z1 1,825z2 2,0875z3 . При этом R2 0,984952 .

Найдем отдельные уравнения для каждого квартала. Для этого оформите фрагмент листа, как показано ниже:

Формулы внесите согласно таблице:

124

Итак, имеем уравнения для каждого квартала:

I квартал – yˆt 6,2375 0,1875t , II квартал – yˆt 3,85 0,1875t , III квартал – yˆt 4,4125 0,1875t , IV квартал – yˆt 8,325 0,1875t .

Расстояние между линией регрессии каждого квартала и трендом дает оценку сезонной компоненты в квартале.

Оформите фрагмент листа, как показано ниже:

и заполните ячейки

Поскольку сумма сезонных компонент равна нулю, мы убедились в правильности решения задачи.

Задача 10.3. Определить коэффициенты автокорреляции до четвертого порядка включительно по данным предыдущей задачи 10.2.

На «Листе2» скопируйте ячейки А2:В18 в буфер, затем перейдите на «Лист3», щелкните по ячейке А2 и вставьте содержимое из буфера. В ячейках D3, D5, D7, D9 введите соответственно r1 , r2 , r3 , r4 .

125

Для нахождения коэффициента автокорреляции 1-го порядка, проделайте следующее: щелкните по ячейке С3, где будет выводиться его значение, выполните последовательность команд меню: Формулы fx

Вставить функцию Статистические КОРРЕЛ ОК, заполнив

Аргументы функции как указано на рис.10.1:

.

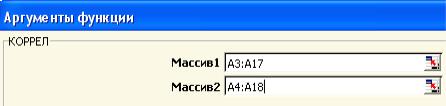Рис.10.1

Нажмите ОК.

Внимание! Поскольку мы находим коэффициенты автокорреляции первого порядка, то Массив1 и Массив2 сдвинуты друг относительно друга на 1 ячейку.

В ячейке Е3 отобразится найденное значение. В ячейках Е5, Е7, Е9 найдите описанным выше способом коэффициенты автокорреляции 2-го, 3-го, 4-го порядков, учитывая, что при этом сдвиг массивов будет осуществляться на 2, 3, 4 ячейки соответственно.

Анализ значений коэффициентов автокорреляции позволяет сделать вывод о наличии во временном ряде линейной тенденции и сезонных колебаний с периодичностью 4 квартала.

Вопросы для самопроверки

1.Охарактеризуйте модели с фиктивными независимыми переменными.

2.Каковы основные факторы, образующие временной ряд?

3.Охарактеризуйте стационарные временные ряды.

4.Что такое «белый шум»?

5.Допустимо ли использование классической модели линейной регрессии для анализа временных рядов?

6.Что такое модели скользящей средней?

7.Что такое модели авторегрессии?

Лабораторная работа №11

Тема: Системы одновременных уравнений

В предыдущих лабораторных работах были рассмотрены модели парной и множественной линейной регрессий, при изучении которых рассматривались односторонние стохастические причинные отношения

126

того, что переменная Y объяснялась переменными X1, X2,..., Xp, которые не находятся под влиянием Y и их можно изменять независимо друг от друга. Было отмечено, что для оценки параметров уравнения используется МНК. Однако ряд экономических процессов моделируется не одним, а несколькими уравнениями, т.е. описывает модель системой уравнений. Различают системы:

независимых уравнений;

рекурсивных уравнений;

одновременных (взаимозависимых) уравнений.

Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений, называемая системой одновременных уравнений (СОУ). В ней в одних уравнениях определенная переменная рассматривается как объясняющая (независимая), но в то же время она входит в другое уравнение как объясняемая (зависимая) переменная. Таким образом, под системой одновременных уравнений понимается набор взаимосвязанных регрессионных моделей, в которых одни и те же переменные могут одновременно играть роль объясняемых переменных (факторов) и объясняющих переменных.

Говоря об эконометрической модели, предполагается, что это система одновременных линейных алгебраических уравнений, часть которых содержит случайные составляющие. В общем виде система одновременных уравнений может быть записана в следующем виде:

Наиболее широко система одновременных уравнений используется для построения макроэкономических моделей функционирования экономики той или иной страны. Большинство из них представляют собой модели кейнсианского типа с той или иной мерой сложности. Например, статистическая модель Кейнса для описания народного хозяйства страны в период t в наиболее простом варианте имеет вид:

127

где Ct – личное потребление в постоянных ценах в период t; Yt – национальный доход в постоянных ценах в период t;

It – инвестиции в постоянных ценах в период t;– случайная составляющая;и – неизвестные коэффициенты модели.

Параметр характеризует предельную склонность к потреблению и не может быть больше 1. Если > 1, то Yt < Ct + It, т.е. на потребление расходуются не только доходы, но и сбережения. Параметр можно истолковать как прирост потребления во времени за счет других факторов. Он может быть положительным или отрицательным.

Во втором уравнении системы отсутствует ошибка, и коэффициенты при объясняющих переменных равны единице.

Рассмотрение систем одновременных уравнений указывает на недостаточность принятого ранее разделения переменных на объясняющие и зависимую, поскольку одна и та же переменная может входить в одно из уравнений как зависимая, а в другое – как объясняющая. Поэтому в эконометрической модели переменные делятся на два больших класса – эндогенные и экзогенные.

1. Эндогенные (внутрисистемные) переменные. Эндогенными переменными являются экономические величины, которые объясняются эконометрической моделью. Значения эндогенных переменных формируются в результате одновременного взаимодействия переменных, образующих модель. Между эндогенными переменными и ошибками, как правило, имеется корреляция.

2. Экзогенные (внесистемные) переменные. Значения экзогенных переменных в каждый период времени t определяются вне модели. Экзогенные переменные являются внешними, наперед заданными экономическими величинами. Они, следовательно, объясняются не моделью, а экономическими факторами и закономерностями, лежащими за границами этой модели. Экзогенные переменные отличаются от эндогенных тем, что в каждом уравнении они не коррелированны с соответствующей ошибкой. Они определяют эндогенные переменные, но сами не находятся под их влиянием. Таким образом, между эндогенными и экзогенными переменными существуют односторонние стохастические причинные отношения. При каждой спецификации эконометрической модели следует заново обстоятельно обсудить проблему разделения

128

переменных, чтобы определить, является ли переменная экзогенной или эндогенной. Деление переменных на экзогенные и эндогенные относительно. Оно зависит от природы изучаемого явления, а также от цели, с которой эта модель строится.

3. Предопределенные переменные. Эндогенные и экзогенные переменные могут быть также лаговыми. Под лаговой переменной понимают переменную, значения которой отстают на один или несколько периодов. При наличии в модели лаговых эндогенных и экзогенных переменных значение эндогенной переменной в период времени t зависит от своих собственных значений в предшествующие периоды, так и от значений экзогенных переменных в те же периоды. В связи с этим к классу предопределенных переменных относят:

обычные экзогенные переменные; они заранее предопределены, так как объясняются не эконометрической моделью, а факторами, лежащими вне этой модели;

лаговые экзогенные переменные; они заранее предопределены, так как их значения принадлежат предшествующим периодам и объясняются вне модели;

лаговые эндогенные переменные; их предопределенность следует из предшествующего объяснения в эконометрической модели.

Вмодели (11.1) переменные С и Y являются эндогенными, которые принимают свои значения в уравнении функции потребления и тождества для совокупного дохода. Они оцениваются внутри модели. Переменная I задается (определяется) вне модели, поэтому она является экзогенной. Модель не объясняет, как получаются значения этой переменной, она просто их использует.

Взависимости от постановки экономической проблемы и цели исследований эконометрическая модель может быть представлена в различных формах:

структурная форма модели – это система уравнений, в каждом из которых помимо объясняющих (независимых) переменных могут содержаться объясняемые (зависимые) переменные из других уравнений.

Уравнения, составляющие исходную модель, называются структурными уравнениями модели, а параметры (коэффициенты) структурной формы модели – структурными коэффициентами;

приведенная форма модели – система уравнений, в каждом из

129

предопределенные переменные и случайные составляющие. Коэффициенты приведенной формы модели называются приведенными коэффициентами. Они оцениваются обычным методом наименьших квадратов, поскольку предопределенные переменные не коррелированы со случайными членами.

Например, разрешая структурную систему (11.1) относительно эндогенных переменных, можно получить приведенную систему уравнений:

В системе уравнений (11.2) коэффициенты при переменной It, равные/(1– ) и /(1– ), представляют собой инвестиционные мультипликаторы потребления и дохода соответственно. Они показывают: если объем инвестиций возрастает на 1, то объем потребления увеличится на /(1– ), а совокупный доход возрастает на 1/(1– ).

Идентификация структурной модели состоит в оценке ее коэффициентов по выборочным данным.

Структурный коэффициент называется идентифицируемым, если его можно вычислить на основе приведенных коэффициентов, причем точно идентифицируемым, если он имеет единственную оценку, и сверхидентифицируемым, если он имеет несколько разных оценок. В противном случае он называется неидентифицируемым.

Какое-либо структурное уравнение является идентифицируемым, если идентифицируемы все его коэффициенты. Если хотя бы один структурный коэффициент неидентифицируем, то и само уравнение является неидентифицируемым.

Модель считается идентифицируемой, если каждое ее уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель неидентифицируема.

Для быстрого формального решения проблемы идентифицируемости структурных уравнений и модели в целом применяется необходимое и достаточное условия идентификации.

130