2.3. Плоская волна

Плоской называется такая звуковая волна, фронт которой представляет собой плоскость, перпендикулярную направлению распространения волны. Звуковые лучи, которые должны быть перпендикулярны фронту волны, будут направлены в этом случае параллельно друг другу. Это указывает на то, что звуковая энергия не расходится в пространстве, а распространяется пучком, т.е. мы имеем случай направленного излучения.

Плоская волна может возникнуть в том случае, если размеры излучателя больше длины излучаемой волны. Это условие выполняется при работе громкоговорителя на верхних звуковых частотах. Плоскую волну можно создать искусственно, нагрузив громкоговоритель на трубу с жесткими стенками. Стенки трубы не дадут волне расходится даже, если размеры излучателя будут меньше длины волны.

Для установления свойств плоской волны определим связь между давлением и колебательной скоростью в ней. Представим излучатель в виде жесткого поршня, колеблющегося вдоль некоторой оси х и излучающего плоскую волну.

Звуковое поле в точке у поверхности источника, излучающего гармоническое колебание, определится как: p=pme^j^^t.

В точке на некотором удалении от излучателя давление запоздает по фазе на время (2.9) и станет равнымp=pme^j^^t-^^).

Решение волнового уравнения

Основная статья: Формула Кирхгофа

Существует аналитическое решение гиперболического уравнения в частных производных. В евклидовом пространстве произвольной размерности оно называется формулой Кирхгофа. Частные случаи: для колебания струны () —формула Д’Аламбера, для колебания мембраны () —формула Пуассона.

Формула д'Аламбера

Решение одномерного волнового уравнения (здесь — фазовая скорость)

(функциясоответствует вынуждающей внешней силе)

с начальными условиями

имеет вид

Интересно заметить, что решение однородной задачи

имеющее следующий вид

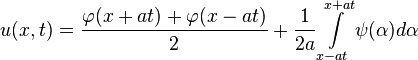
может быть представлено в виде

где

В таком случае говорят, что решение представлено в виде суммы бегущих волн, а функции и- это профили волн, бегущих, соответственно, влево и вправо. В рассматриваемом случае профили волн со временем не изменяются.

В многомерном случае также решение задачи Коши может быть разложено в бегущие волны, однако уже не в сумму, а в интеграл, поскольку направлений становится бесконечно много. Это делается элементарно при помощи преобразования Фурье

5 плотность потока энергии звуковой волны. Акустическое сопротивление

Плотностью потока энергии — средняя по времени энергия, которую электромагнитная или звуковая волна переносит в единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны

Через площадку S за время будет перенесена энергиязаключенная в цилиндре с основанием S и высотой. Если размеры цилиндра достаточно малы (за счет малости S и) для того, чтобы плотность энергии во всех точках цилиндра можно было считать одинаковой, то можно найти как произведение плотности энергии w на объем цилиндра, S ии тогда получается, что энергия равна: