
Методические указания по математическому анализу (часть 2)
Пример
1 Дана функция двух переменных
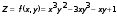 .
Найти все частные производные первого
и второго порядков.
.
Найти все частные производные первого
и второго порядков.
Решение : Частные производные от функции нескольких переменных по одной из переменных находятся в предположении, что другие переменные являются постоянными величинами. Таким образом, функция нескольких переменных становится обычной функцией одной переменной, к которой применяются все известные правила дифференцирования функции одной переменной.
Требуется
найти
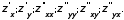 Положим
Положим

Находим
производную функции
 по переменной
по переменной
 :
:

Полагая
 ,
находим первую производную функции
,
находим первую производную функции
 по переменной y:
по переменной y:

Теперь
найдем производные второго порядка.
Возьмем первую производную по
 , считая
, считая
 постоянным, продифференцируем еще раз
по
постоянным, продифференцируем еще раз
по
 .
.
Получим
 .
Если, считая x
постоянным, мы продифференцируем
.
Если, считая x
постоянным, мы продифференцируем
 ещё раз, но уже по y,
то получим
ещё раз, но уже по y,
то получим
 .
.
Теперь
возьмем первую производную по
 и считая x постоянным,
продифференцируем
и считая x постоянным,
продифференцируем
 еще раз по y. Мы получим
еще раз по y. Мы получим
 .
.
Если
мы, взяв
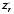 ,
и считая y постоянным,
продифференцируем
,
и считая y постоянным,
продифференцируем
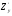 еще раз, но по переменной x
получим
еще раз, но по переменной x
получим
 .
.
Обратим
внимание, что
 ;
это равенство справедливо при условии
непрерывности данных производных.
;
это равенство справедливо при условии
непрерывности данных производных.
Пример
2. Даны функции
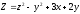 и точка М(1,02;2,05). С помощью полного
дифференциала вычислить приближенное
значение функции в точке М и оценить
относительную погрешность.
и точка М(1,02;2,05). С помощью полного
дифференциала вычислить приближенное
значение функции в точке М и оценить
относительную погрешность.
Решение: Приближенное значение некоторой функции f(x,y) в точке (x,y) с помощью полного дифференциала находится по формуле (*)
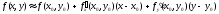 ,
,
где
 ,
значение функции f(x,y)
в точке
,
значение функции f(x,y)
в точке
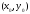 .
.
Точка
 подбирается
таким образом, чтобы
подбирается
таким образом, чтобы
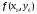 легко
вычислялось;
легко
вычислялось;
 ,
,
 приращение
функции f(x,y)
в точке
приращение
функции f(x,y)
в точке
 по
переменным x и y
соответственно.
по
переменным x и y
соответственно.
В качестве точки
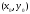 возьмем
точку N(1,2), так как
значение x и y
в точке N целые и точка
N близка к данной точке
M.
возьмем
точку N(1,2), так как
значение x и y
в точке N целые и точка
N близка к данной точке
M.
Тогда
 в
точке
в
точке
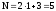
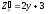 в
точке
в
точке

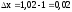

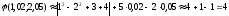
Вычислим точное значение
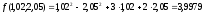
Итак, принимая вместо
точного значения 3,9979 значение
 ,
мы допускаем абсолютную погрешность
,
мы допускаем абсолютную погрешность
 или относительную погрешность
или относительную погрешность
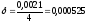
Пример
3. Найти наибольшее и наименьшее
значение функции
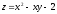 в ограниченной замкнутой области D:
в ограниченной замкнутой области D:

Решение:
Точка
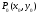 являются точкой экстремума
(максимума или минимума) функции
z=f(x,y),
если значение функции в этой точке
соответственно больше или меньше
значений, принимаемых ее в некоторой
окрестности точки
являются точкой экстремума
(максимума или минимума) функции
z=f(x,y),
если значение функции в этой точке
соответственно больше или меньше
значений, принимаемых ее в некоторой
окрестности точки
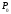 ,
то есть при всех x и y
достаточно близких к
,
то есть при всех x и y
достаточно близких к
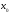 и
и
 .
Точка P, координаты
которой обращают в нуль обе частные
производные функции f(x,y)
называются стационарной точкой этой
функции.
.
Точка P, координаты
которой обращают в нуль обе частные
производные функции f(x,y)
называются стационарной точкой этой
функции.
-
Найдем стационарные точки функции z(x,y)


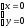
Стационарная точка y функции z одна. Это точка 0.
-
Входит ли точка (0,0) в область D? Построим эту область.
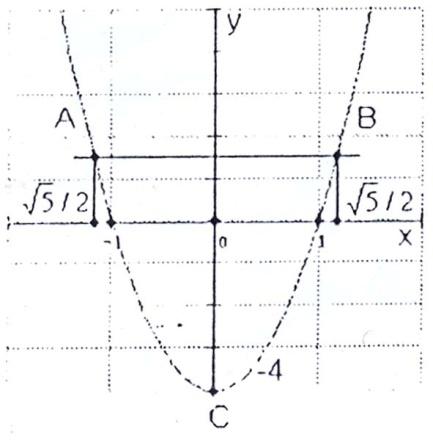
-
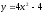 - парабола с вершиной в точке (0,-4).
Точки пересечения с осью x:
- парабола с вершиной в точке (0,-4).
Точки пересечения с осью x:
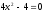 ,
,
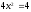 ,
,
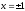
- y=0 – ось x.
Точка (0,0) входит
в область D. Установим,
является ли стационарная точка 0
точкой экстремума. Это делается так:
Пусть
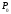 стационарная точка функции z=f(x,y).
Вычислим в этой точке
стационарная точка функции z=f(x,y).
Вычислим в этой точке
 .
.
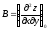 .
.
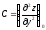
Если
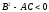 ,
то функция f(x,y)
имеет в точке
,
то функция f(x,y)
имеет в точке
 экстремум:
экстремум:
max-при A<0 и min при A>0.
Если
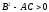 ,
то точка
,
то точка
 не
является точкой экстремума.
не
является точкой экстремума.
Если
 ,
то требуется дополнительное исследование.
,
то требуется дополнительное исследование.
Исследуем нашу функцию z по формулам.
3.
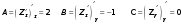
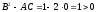 ,
точка (0,0) не является точкой экстремума.
,
точка (0,0) не является точкой экстремума.
4. Исследуем поведение функции на границе.
Так как Z не имеет ни max ни min, ее наибольшим и наименьшем значением является наибольшее и наименьшее из значений, принимаемых на границе.
Для того, чтобы найти наибольшее или наименьшее из значений, принимаемых на границе.
4а.
Рассмотрим верхнюю границу y=1.
На ней функция Z(x,1)
превращается в
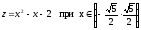
 ,
,
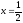 в этой точке возможен экстремум. Знак
производной меняется с – на +, то есть
в точке
в этой точке возможен экстремум. Знак
производной меняется с – на +, то есть
в точке
 - минимум z =-2.25
- минимум z =-2.25
при
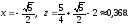
В точке
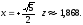
4б. Рассмотрим
нижнюю границу
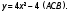

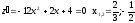
В точке
 производная меняет знак с - на +,
следовательно, это точка минимума
производная меняет знак с - на +,
следовательно, это точка минимума

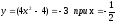
В точке
 производная меняет знак с + на -,
следовательно, это точка максимума
производная меняет знак с + на -,
следовательно, это точка максимума
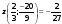 .
При
.
При
 функция z уже вычислялось.
Видим, что от
функция z уже вычислялось.
Видим, что от
 функция
убывает до
функция
убывает до
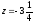 ,
затем возрастает до
,
затем возрастает до
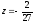 а затем убывает до
а затем убывает до
 .
.
То есть наименьшее
значение для всей границы
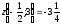 ,
а наибольшее
,
а наибольшее
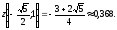
Ответ: Наибольшее
значение функции z в
замкнутой области D
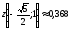 ,
наименьшее
,
наименьшее
 .
.
Пример
4. Даны функция трех переменных
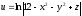 ,
вектор
,
вектор
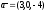 и точка
и точка
 .
.
Найти: 1) Grad u в точке M0;
2)
производную в точке M0
по направлению вектора
 ;
;
Решение:
1)
Вектором градиентом функции трех
переменных u(x,y,z)
является вектор
grad
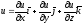 (или
(или
 в случае двух переменных)
в случае двух переменных)
Найдем частные произведения функции u:



Из определения градиента следует, что эти частные производные являются проекциями вектора-градиента на оси координат. Вычислим значения частных производных в точке Mo.
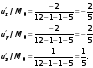
Следовательно вектор-градиент в точке M0 имеет вид:

2)
Производная по направлению вектора
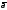 вычисляется
по формуле
вычисляется
по формуле
 ,
то есть равна скалярному произведению
вектора градиента на единичный вектор,
совпадающий по направлению с вектором
,
то есть равна скалярному произведению
вектора градиента на единичный вектор,
совпадающий по направлению с вектором
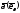 .
.
Так
как
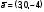 ,
то его длина
,
то его длина
 и, следовательно, единичный вектор,
совпадающий по направлению с
и, следовательно, единичный вектор,
совпадающий по направлению с
 ,
,
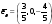 ,
используя формулу скалярного произведения
в координатной форме
,
используя формулу скалярного произведения
в координатной форме
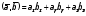 ,
получим
,
получим

Итак
производная функции u
по направлению вектора
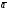 равна
равна
 .
.
Пример 5. Докажем
сходимость ряда
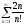 .
Для этого ряда имеем
.
Для этого ряда имеем
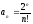 ,
,
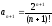 .
Значит,
.
Значит,

Так как
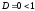 ,
то ряд сходится.
,
то ряд сходится.
Пример 6
Исследовать
сходимость ряда (А):

Решение.
Для ряда (А*), составленного из абсолютных
величин рассматриваемого ряда, общий
член
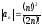 .
Применяем к ряду (А*) признак Даламбера:
.
Применяем к ряду (А*) признак Даламбера:
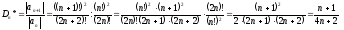
 .
.
Ряд (А) сходится абсолютно.
Пример
7. Определить область (абсолютной и
условной) сходимости функционального
ряда:
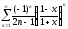 .
.
Решение.
При каждом значении
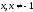 имеем
обычный числовой ряд. Применяем к
нему признак Даламбера, как это делалось
при исследовании абсолютной сходимости.
Вводим величину:
имеем
обычный числовой ряд. Применяем к
нему признак Даламбера, как это делалось
при исследовании абсолютной сходимости.
Вводим величину:
 .
.
Отыскиваем предел
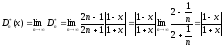 .
.
Для тех значений
 ,
при которых
,
при которых
 ,
рассматриваемый ряд сходится абсолютно.
Для значений
,
рассматриваемый ряд сходится абсолютно.
Для значений
 ,
при которых
,
при которых
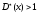 ,
исследуемый ряд расходится, (общий член
не стремится к нулю). Точки, для которых
,
исследуемый ряд расходится, (общий член
не стремится к нулю). Точки, для которых
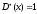 ,
подлежат специальному рассмотрению,
так же как и точки, для которых нельзя
было составить величину
,
подлежат специальному рассмотрению,
так же как и точки, для которых нельзя
было составить величину
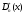 .
В данном примере это точки
.
В данном примере это точки
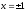 .
Сразу отметим, что при
.
Сразу отметим, что при
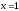 ряд состоит из одних нулей и, очевидно,
является абсолютно сходящимся, а при
ряд состоит из одних нулей и, очевидно,
является абсолютно сходящимся, а при
 ряд не определен. Решим неравенство
ряд не определен. Решим неравенство

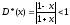 .
.
Это неравенство
равносильно следующему:
 .
Но
.
Но
 -
расстояние от точки
-
расстояние от точки
 до точки
до точки
 ,
а
,
а
 - расстояние от точки
- расстояние от точки
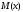 до
до
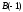 .
Так как начало координат равноудалено
от точек А и В, то неравенство
|МА| < |МВ| выполняется, если точка
М лежит на положительной полуоси, т.е.
если
.
Так как начало координат равноудалено
от точек А и В, то неравенство
|МА| < |МВ| выполняется, если точка
М лежит на положительной полуоси, т.е.
если
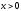 .
При
.
При
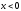 имеем
имеем
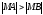 ,
и потому
,
и потому
 а поэтому ряд расходится.
а поэтому ряд расходится.
При
 имеем
имеем
 ,
и потому эту точку рассматриваем
отдельно. Получаем ряд:
,
и потому эту точку рассматриваем
отдельно. Получаем ряд:
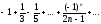 ,
который сходится условно.
,
который сходится условно.
Итак, областью
сходимости ряда является числовой луч:
[0;
 ).
При:
).
При:
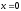 исследуемый ряд сходится условно, а в
остальных точках луча: [0;
исследуемый ряд сходится условно, а в
остальных точках луча: [0;
 )
- абсолютно.
)
- абсолютно.
Для отыскания области
сходимости этого ряда можно было
применить признак Коши (радикальный).
В этом случае вводится последовательность
 и
отыскивается предел
и
отыскивается предел
 (если
он существует). Далее решается неравенство
(если
он существует). Далее решается неравенство
 .
На множестве, являющемся егo
решением, ряд сходится абсолютно. Там,
где
.
На множестве, являющемся егo
решением, ряд сходится абсолютно. Там,
где
 ,
ряд расходится (общий член не стремится
к нулю). Точки, в которых
,
ряд расходится (общий член не стремится
к нулю). Точки, в которых
 ,
требуют отдельного рассмотрения.
,
требуют отдельного рассмотрения.
Пример 8. Найдем
область сходимости ряда
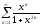 .
.
Решение. Применяем признак Даламбера. Имеем:
 .
.
Далее

Если
 |,
тогда
|,
тогда
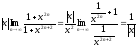 .
.
Из выражения для
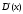 следует, что и при
следует, что и при
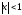 и при
и при
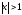 |
исследуемый ряд сходится абсолютно.
Заметим, что при
|
исследуемый ряд сходится абсолютно.
Заметим, что при
 признак
Даламбера не применим, но в этом случае
ряд состоит из нулей и его абсолютная
сходимость тривиальна.
признак
Даламбера не применим, но в этом случае
ряд состоит из нулей и его абсолютная
сходимость тривиальна.
Далее
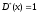 при
при
 ,
но в этих точках общий член ряда по
абсолютной величине равен
,
но в этих точках общий член ряда по
абсолютной величине равен
 ,
и потому ряд расходится.
,
и потому ряд расходится.
Итак, во всех точках
числовой оси, кроме
 ,
рассматриваемый ряд сходится и притом
абсолютно.
,
рассматриваемый ряд сходится и притом
абсолютно.
Пример 9.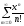 .
.
Решение.
Применим признак Даламбера
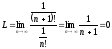 .
.
Следовательно,
 и данный ряд сходится на всей числовой
оси.
и данный ряд сходится на всей числовой
оси.
Пример 2.

Решение.
Применим признак Коши
 .
.
Следовательно,
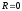 и ряд сходится только в точке
и ряд сходится только в точке
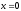 .
.
Пример 10.
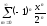 .
.
Решение.
 .
.
Следовательно,
 и ряд сходится на интервале
и ряд сходится на интервале
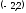 .
Исследуем сходимость ряда на концах
интервала.
.
Исследуем сходимость ряда на концах
интервала.
1). Пусть
 .
.
Получим числовой
ряд
 .
Этот ряд расходится.
.
Этот ряд расходится.
2). Пусть
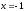 .
.
Получим числовой ряд
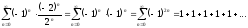
Этот ряд также расходится.
Таким образом,
степенной ряд сходится только внутри
промежутка
 .
.
Пример
11 Найти
частное решение дифференциального
уравнения
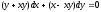 ,
при условии
,
при условии
 .
.
Решение:
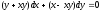 ;
;
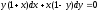 ─ уравнение
с разделяющимися переменными.
─ уравнение
с разделяющимися переменными.
Разделим
обе части уравнения на
xy,
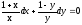 .
.
Интегрируя,
получим:
 ;
;
 ;
;
 ;
;
 ─ общее решение.
─ общее решение.
y(1)=1;
ln1+1-1=c;
c=0;
частное решение
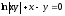 .
.
Пример 12 Найти общее решение дифференциального уравнения
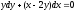
Решение:
Обозначим
 ,
,
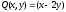 и
проверим, являются ли эти функции
однородными одной степени.
и
проверим, являются ли эти функции
однородными одной степени.
 ;
;
 ,
,
 и
и
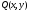 однородные функции степени 1, данное
уравнение является однородным.
однородные функции степени 1, данное
уравнение является однородным.
Применим
подстановку
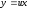 ,
,
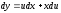 ;
;
 ;
разделим обе части уравнения на x,
;
разделим обе части уравнения на x,
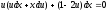 ;
;
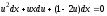 ;
;
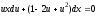 .
.
Получили уравнение с разделяющимися переменными.
 ;
;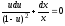 ;
;
 ;
;
 ;
;
 .
.
Вместо
u,
в полученное
решение,
подставим
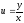
 ;
; ;
;
 ;
;
 ─ общее
решение уравнения.
─ общее
решение уравнения.
Пример
13 Найти
общее решение уравнения
 .
.
Решение:
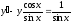 ─ уравнение линейное.
─ уравнение линейное.
Применим
подстановку
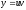 ;
;

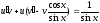 ;
найдем v
из уравнения
;
найдем v
из уравнения
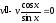 ;
;
 ;
;
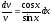 ;
; ;
;
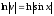 ;
;
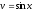 .
.
Функцию u найдём из уравнения
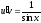 ;
;
 ;
; ;
;
 ;
; 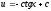 .
.
Искомую
функцию y
находим из
равенства

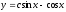 ─ общее
решение.
─ общее
решение.
Пример
14 Найти
общее решение уравнения
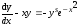 .
.
Решение:
 ─
уравнение Бернулли.
─
уравнение Бернулли.
Разделим
обе части уравнения на
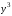 ,
,
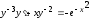 .
.
Введём
замену

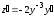 ;
;
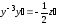 и подставим в данное уравнение
и подставим в данное уравнение
 .
Получили линейное уравнение.
.
Получили линейное уравнение.
Введём
замену
 ;
;
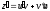 ;
;
 ;
;
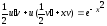 ;
;
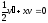 ;
;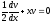 ;
;
 ;
;
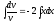 ;
;
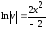 ;
; ;
;
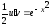 ;
;
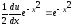 ;
;
 ;
;
 ;
;
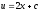 .
.
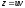 ;
;
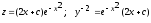 ;
;
 ─ общее
решение.
─ общее
решение.
Решение однородного линейного дифференциального уравнение 2-го порядка с постоянными коэффициентами
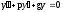 линейное
однородное дифференциальное уравнение
2-го порядка.
линейное
однородное дифференциальное уравнение
2-го порядка.
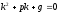 характеристическое
уравнение.
характеристическое
уравнение.
|
Корни характеристического уравнения |
Вид решения |
|
1. k1, k2 – действительные различные корни |
|
|
2. k=k1=k2; k1, k2 – действительные равные корни |
|
|
3.
k1,
2= k1, k2-комплексные корни |
|
Пример 15
 ;
;
Характеристическое
уравнение
 ;
k1=1,
k2=2;
;
k1=1,
k2=2;
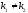
Общее
решение
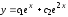
Пример 16
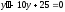 ;
;
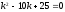 ;
;
 ;
;
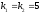
Общее
решение
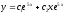
Пример 17
 ;
;
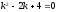 ;
;
 ;
;
 ,
,
Общее
решение ─
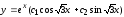 .
.
Решение неоднородного линейного уравнения 2-го порядка с постоянными коэффициентами
 ─
линейное
неоднородное дифференциальное уравнение
2-го порядка с постоянными коэффициентами
p
и g.
─
линейное
неоднородное дифференциальное уравнение
2-го порядка с постоянными коэффициентами
p
и g.
Общее решение неоднородного уравнения имеет вид

 ─
общее
решение соответствующего однородного
уравнения;
─
общее
решение соответствующего однородного
уравнения;
 ─
частное
решение неоднородного дифференциального
уравнения.
─
частное
решение неоднородного дифференциального
уравнения.
Для
подбора частного решения
 по виду правой части f(x)
и корней характеристического уравнения
можно пользоваться следующей таблицей.
по виду правой части f(x)
и корней характеристического уравнения
можно пользоваться следующей таблицей.
Рассмотрим только те случаи, в которых корни характеристического уравнения – действительные числа.
|
Правая часть уравнения f(x) |
Корни характеристическо-го уравнения |
Вид частного решения уравнения |
|
1.
|
а)
т.е
|
|
|
б)
|
|
|
|
в)
|
|
Пример
18
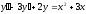
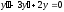 однородное
дифференциальное уравнение 2-го порядка.
однородное
дифференциальное уравнение 2-го порядка.
Правая
часть
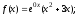
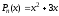 ─ многочлен 2-ой степени,
─ многочлен 2-ой степени,
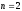 .
.
Найдём общее решение соответствующего однородного уравнения.
 характеристическое
уравнение;
характеристическое
уравнение;
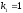 ;
;
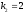 ─ корни уравнения различные, общее
решение соответствующего однородного
уравнения ─
─ корни уравнения различные, общее
решение соответствующего однородного
уравнения ─

Найдём частное решение неоднородного дифференциального уравнения,
т.
к.
 не является корнем характеристического
уравнения, т. е.
не является корнем характеристического
уравнения, т. е.
 ,
,
 ,
то вид частного решения
,
то вид частного решения
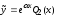 ;
;
 ;
;
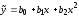 .
Найдём
.
Найдём
 ;
;
 и подставим полученные выражения
и подставим полученные выражения
 в исходное уравнение
в исходное уравнение
 ;
;
 ;
;
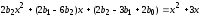
Приравниваем коэффициенты при соответствующих степенях x в левой и правой частях уравнения

 ,
решая систему, получим
,
решая систему, получим
 .
.
Тогда
частное решение

Общее решение неоднородного дифференциального уравнения имеет вид
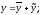
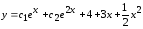 .
.
Пример 19
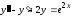
 ;
;
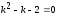 ;
;
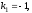
 ;
;
 ,
,
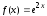 ;
;
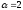 ;
;
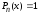 −
многочлен нулевой степени,
−
многочлен нулевой степени,
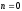 ,
,
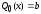 ;
;
 корень характеристического уравнения,
следовательно, частное решение будем
искать в следующем виде:
корень характеристического уравнения,
следовательно, частное решение будем
искать в следующем виде:
 ;
;
 ;
;
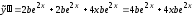 ;
;
 ;
;
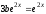 ;
;
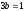 ;
;
 ;
;
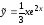 .
Общее решение
.
Общее решение
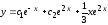 .
.
Пример 20
 .
.
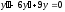 ;
;
 ;
;
 ;
;
 ,
,
 ─ общее
решение соответствующего однородного
уравнения.
─ общее
решение соответствующего однородного
уравнения.
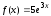 0,
0,
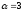 ─ двукратный корень характеристического
уравнения
─ двукратный корень характеристического
уравнения
 ,
n=0,
,
n=0,
 ,
,
 ;
;
 ;
;
 ;
;


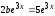 ;
;
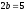 ;
;
 ;
;
 .
.
Общее
решение ─
 .
.
Пример
21 Исследовать
ряд на сходимость а) 
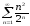 б)
б)

Решение:
а)
 ,
,
 ;
;
 ;
;
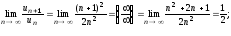
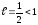 по
признаку Даламбера ряд сходится;
по
признаку Даламбера ряд сходится;
б)
 ,
,
 .
По признаку Даламбера
.
По признаку Даламбера

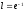 <
1, ряд сходится.
<
1, ряд сходится.

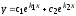
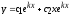
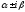
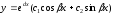

 ─
действительное
число
─
действительное
число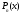 ─
многочлен степени
n>0 относительно
x.
─
многочлен степени
n>0 относительно
x.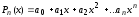
 ─
не является корнем характеристическо-го
уравнения,
─
не является корнем характеристическо-го
уравнения,

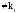 ,
,

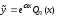
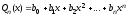
 ─ является корнем характеристическо-го
уравнения
─ является корнем характеристическо-го
уравнения =
=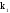 ,
,

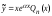
 ─ является двукратным корнем
характеристичес-кого уравнения
─ является двукратным корнем
характеристичес-кого уравнения

