
- •85 Тишин в. И. Основные методы решения тригонометрических уравнений
- •Тригонометрические уравнения
- •1. Метод разложения на множители
- •Пример 12. Решить уравнение
- •Задание 1
- •2. Метод замены переменных и сведение к алгебраическим уравнениям
- •2.1. Применение формул двойного и половинного аргумента
- •2.2. Применение формул приведения
- •Задание 2
- •3. Уравнения, однородные относительнои
- •3.1. Применение формул приведения
- •Задание 3
- •Задание 4
- •4. Метод замены переменных
- •4.1. Замена.
- •Задание 5
- •4.2. Замена
- •4.3. Случаи, когда в уравнении не содержится
- •4.4. Случаи, когда аргументы кратны 2x и X
- •Задание 6
- •4.5. Замена. Универсальная тригонометрическая подстановка
- •Задание 7
- •5. Метод оценки левой и правой частей уравнения
- •Задание 8
- •6. Введение вспомогательного аргумента
- •Задание 9
- •7. Системы тригонометрических уравнений
- •Задание 10
4.3. Случаи, когда в уравнении не содержится
Пример
132.
Решите уравнение
![]() .
.
Решение
Область
допустимых значений:
 .
.
Выполним
замену:
 ,
получим:
,
получим:
![]()
![]() ;
;
![]() -
не удовлетворяет условию
-
не удовлетворяет условию
![]() .
.
Определим значения x, которые входят в область допустимых значений.
Сразу ясно, что вторая группа корней не входит в область допустимых значений. Проверим первую группу корней:
 -
это значит, что все значения из множества
-
это значит, что все значения из множества
 входят в область допустимых значений.
входят в область допустимых значений.
Ответ:
 .
.
Пример
133.
Решите уравнение
![]() .
.
Решение
Область
допустимых значений:
![]() .
.
Выразим:
 ,
получим:
,
получим:

![]() -
не удовлетворяет условию
-
не удовлетворяет условию
![]() и является посторонним корнем.
и является посторонним корнем.
![]() -
удовлетворяет уравнению.
-
удовлетворяет уравнению.
![]() -
эти значения входят в область допустимых
значений.
-
эти значения входят в область допустимых
значений.
Ответ:
![]() .
.
Пример
134.
Решите уравнение
![]() .
.
Решение
Выразим:
 ,
получим:
,
получим:
 .
.
Возведем обе части уравнения в квадрат, получим:

 .
.
Ответ:
![]() .
.
Пример
135.
Решите уравнение
![]() .
.
Решение
Выразим:
 ,
получим:
,
получим:
![]() .
Возведем обе части уравнения в куб,
получим:
.
Возведем обе части уравнения в куб,
получим:
![]()
![]()
![]()

 .
.
Ответ:
![]() .
.
4.4. Случаи, когда аргументы кратны 2x и X
Пример
136.
Решите уравнение
![]() .
.
Решение
Преобразуем
уравнение, используя формулу:
![]() ,
отсюда находим:
,
отсюда находим:![]() ,
получим уравнение:
,
получим уравнение:
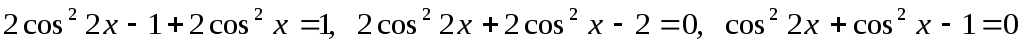 .
.
Выполним
замену:
 ,
получим уравнение:
,
получим уравнение:
 .
.

Ответ:
![]()
Пример
137.
Решите уравнение
![]() .
.
Решение
Найдем
область допустимых значений:
 .
.
Преобразуем
уравнение:
![]() .
.
Выполним
замену:
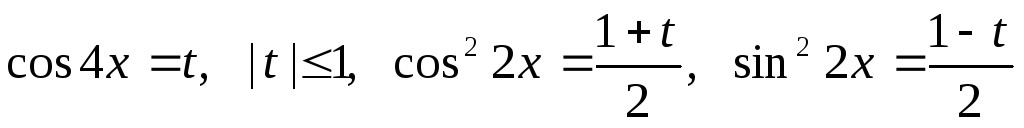 ,
получим:
,
получим:

 -
этот корень не удовлетворяет условию
-
этот корень не удовлетворяет условию
![]() и является посторонним корнем.
и является посторонним корнем.
 .
.
Ответ:
 .
.
Пример
138.
Решите уравнение
![]() .
.
Решение
Область
допустимых значений:
 .
.
Выразим:
 ,
получим:
,
получим:



так
как
![]() .
Разделим обе части уравнения на
.
Разделим обе части уравнения на![]() ,
получим:
,
получим:
![]() .
Это уравнение равносильно совокупности
уравнений:
.
Это уравнение равносильно совокупности
уравнений:

Определим, входят ли значения x в область допустимых значений.
 .
.
Эти неравенства означают, что обе группы корней входят в область допустимых значений.
Ответ:

Задание 6
Решите уравнение:
139.
![]() .140.
.140.
![]() .
.
141.
![]() .142.
.142.
![]() .
.
143.
![]() .144.
.144.
![]() .
.
145.
![]() .
.
4.5. Замена. Универсальная тригонометрическая подстановка
При
такой замене через
![]() нетрудно выразить
нетрудно выразить![]() и
и![]() :
:


Таким образом, мы получаем следующую замену:

Замена
(31),
в частности, может быть применена, если
рассматривается тригонометрическое
уравнение, левая часть которого является
рациональной
функцией
от
![]() и
и![]() ,
т. е. представляется в виде
,
т. е. представляется в виде![]() ,
гдеP
и Q
- некоторые многочлены
от
,
гдеP
и Q
- некоторые многочлены
от
![]() и
и![]() .
.
Замечание.
Замена
![]() сокращает область допустимых значений,
сокращает область допустимых значений,![]() ,
значит, либо уравнение должно иметь
такую о. д. з., либо полученные значения
надо проверить подстановкой в уравнение
,
значит, либо уравнение должно иметь
такую о. д. з., либо полученные значения
надо проверить подстановкой в уравнение![]() .
.
Пример
146.
Решите уравнение![]() .
.
Решение
1-й способ
Область допустимых значений:
![]() ,
так как при m
= 2n
+ 1 получим
,
так как при m
= 2n
+ 1 получим
![]()
Выразим
 ,
получим:
,
получим:



Ответ:
![]() .
.
2-й способ
Область допустимых значений:
 .
.
Преобразуем уравнение:
 ,
,
![]()
![]() .
Полученное уравнение равносильно
системе:
.
Полученное уравнение равносильно
системе:
 .
.
Ответ:
![]() .
.
Пример
147.
Решите уравнение![]() .
.
Решение
Выразим
 ,
,![]() .
.
Значения
![]() не являются решениями данного уравнения,
тогда, подстановка будет корректной,
получим уравнение:
не являются решениями данного уравнения,
тогда, подстановка будет корректной,
получим уравнение:


 .
.
Определим значения переменных, входящих в область допустимых значений.
Очевидно,
что
![]() входят в область допустимых значений
и являются корнями уравнения.
входят в область допустимых значений
и являются корнями уравнения.
![]() -
это неравенство выполняется при любых
целых значениях n
и k,
значит
-
это неравенство выполняется при любых
целых значениях n
и k,
значит
 являются решениями уравнения.
являются решениями уравнения.
Ответ:
![]()
![]() .
.
Пример
148.
Решите уравнение![]() .
.
Решение
Область
допустимых значений:
![]() .
.
Выразим
![]() ,
получим уравнение:
,
получим уравнение:
![]()

Выясним, входят ли эти значения переменной в область допустимых значений:
 .
.
Оба неравенства выполняются при любых целых значениях n, m и k, значит, оба множества корней входят в область допустимых значений.
Ответ:
![]() .
.
Пример
149.
Решите уравнение![]() .
.
Решение
Область
допустимых значений
![]() .
.
Выразим
![]() ,
получим уравнение:
,
получим уравнение:
![]()
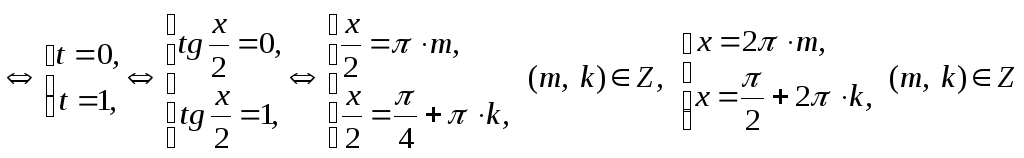 .
.
Выясним, входят ли эти значения переменной в область допустимых значений:
 .
.
Оба неравенства выполняются при любых целых значениях n, m и k, значит, оба множества корней входят в область допустимых значений.
Ответ:
 .
.
Пример
150.
Решите уравнение![]() .
.
Решение
Область
допустимых значений:
![]() .
.
Выразим
![]() ,
получим уравнение:
,
получим уравнение:
![]() .
.
Это
биквадратное уравнение:
![]() ,
,
![]() .
Уравнение
.
Уравнение
![]() не имеет решений, так как правая часть
отрицательна.
не имеет решений, так как правая часть
отрицательна.
![]() .
.
Получим совокупность уравнений:
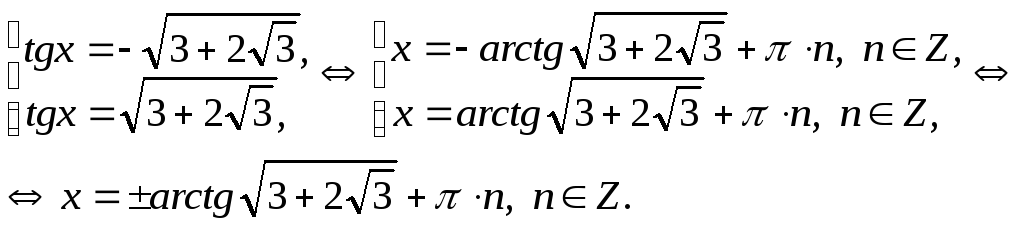
Эти корни входят в область допустимых значений.
Ответ:
![]() .
.
Пример
151.
Решите уравнение![]() .
.
Решение
Область
допустимых значений:
![]() .
.
Выразим
![]() ,
,![]() ,
получим уравнение:
,
получим уравнение:
![]()
![]() .
.
Это
уравнение равносильно совокупности
уравнений:
![]()
Второе уравнение не имеет корней, так как его дискриминант отрицателен.
![]()
Эти корни входят в область допустимых значений.
Ответ:
![]() .
.
Пример
152.
Решите уравнение![]() .
.
Решение
Область
допустимых значений переменной:
![]() .
.
Выразим
![]() ,
получим уравнение:
,
получим уравнение:
![]()
![]()
![]() .
.
Полученное уравнение равносильно совокупности уравнений:
![]() Второе
уравнение совокупности имеет отрицательный
дискриминант и не имеет действительных
корней. Получаем один корень: t
= 1.
Второе
уравнение совокупности имеет отрицательный
дискриминант и не имеет действительных
корней. Получаем один корень: t
= 1.
![]() .
.
Выясним, входят ли эти значения переменной в область допустимых значений:
![]() .
.
Как видим, последнее неравенство выполняется при любых целых значениях n и k, а, значит, корни входят в область допустимых значений.
Ответ:
![]() .
.
Пример
153.
Решите уравнение![]() .
.
Решение
Область
допустимых значений:
![]() .
.
Пусть
![]() ,
тогда
,
тогда![]() ,
получим уравнение:
,
получим уравнение:
![]()
![]() .
.
Полученное уравнение равносильно совокупности уравнений:
![]() Второе,
квадратное уравнение этой совокупности
имеет отрицательный дискриминант и не
имеет действительных корней. Находим:
t
= 1.
Второе,
квадратное уравнение этой совокупности
имеет отрицательный дискриминант и не
имеет действительных корней. Находим:
t
= 1.
![]() .
.
Выясним, входят ли эти значения переменной в область допустимых значений:
![]() .
.
Как
видим, последнее неравенство выполняется
при любых целых значениях n
и k,
а, значит,
![]() входят в область допустимых значений
и являются корнями уравнения.
входят в область допустимых значений
и являются корнями уравнения.
Ответ:
![]() .
.
Пример
154.
Решите уравнение![]() .
.
Решение
Область
допустимых значений:
![]() .
.
Пусть
![]() ,
тогда
,
тогда![]() ,
получим уравнение:
,
получим уравнение:
![]() .
.
Полученное
уравнение равносильно совокупности
уравнений:
![]()
Второе,
квадратное, уравнение этой совокупности
не имеет действительных корней, тогда,
получим:
![]() .
.
Выясним, входят ли эти значения переменной в область допустимых значений:
![]() .
.
Как
видим, последнее неравенство выполняется
при любых целых значениях n
и k,
а, значит,
![]() входят в область допустимых значений
и являются корнями уравнения.
входят в область допустимых значений
и являются корнями уравнения.
Ответ:
![]() .
.
Пример
155.
Решите уравнение![]() .
.
Решение
Область
допустимых значений:
![]() .
.
Пусть
![]() ,
тогда
,
тогда![]() ,
получим уравнение:
,
получим уравнение:
![]()
![]() .
.
Полученное уравнение равносильно совокупности уравнений:
 .
.
Выясним, входят ли эти значения переменной в область допустимых значений.
 .
.
Как видим, эти неравенства выполняются при любых целых значениях n, k и m, следовательно, полученные значения переменной входят в область допустимых значений и являются корнями уравнения.
Ответ:
![]() .
.
Пример
156.
Решите уравнение![]() .
.
Решение
Область
допустимых значений:
![]() .
.
Пусть
![]() ,
тогда
,
тогда![]() ,
получим уравнение:
,
получим уравнение:
![]()
![]()
![]() .
.
![]() .
.
Эти значения переменной входят в область допустимых значений.
Ответ:
![]() .
.
