Задание 1

Решите уравнения

27. .28. .

29. .

30. 31. .

32. 33. .

34. .35. .

36. .37. .

2. Метод замены переменных и сведение к алгебраическим уравнениям

Пример 38. Решите уравнение .

Решение

Преобразуем уравнение. Применим тождество , получим уравнение:

. Положим , получим систему:

,

.

Ответ: .

Пример 39. Решите уравнение .

Решение

Преобразуем уравнение:

,

,

Ответ: .

Пример 40. Решите уравнение.

Решение

Преобразуем уравнение:

. Пусть sin2x = y, , получим

,

.

Ответ: .

Пример 41. Решите уравнение .

Решение

Преобразуем уравнение, используя формулу , получим уравнение:.

Пусть , приходим к системе:

.

.

Ответ: .

Пример 42. Решите уравнение

Решение

Преобразуем уравнение:

.

Положим , получим:

,

.

Ответ: .

2.1. Применение формул двойного и половинного аргумента

Пример 43. Решите уравнение .

Решение

Используем формулу , получим уравнение:

.

Положим , получим,

.

Ответ: .

Пример 44. Решите уравнение .

Решение

Преобразуем уравнение, применив формулу: .

Получим уравнение: .

Пусть , тогда:

,

.

Ответ: .

Пример 45. Решите уравнение.

Решение

Область допустимых значений: .

Преобразуем уравнение:

Из области допустимых значений следует, что приn = 4m - 1 получим: , значит, второе множествоне входит в область допустимых значений.

Проверим первое множество значений:

При получим:

. Совершенно очевидно, что найдутся целые значения n, при которых k будет равняться полученной дроби. Эти значения должны быть исключены из множество решений.

Ответ: ,.

2-й способ

Область допустимых значений: .

Преобразуем уравнение:

.

.

Пусть , получим уравнение,

оба значения удовлетворяют условию

Получим совокупность уравнений:

.

Оба множества значений x входят в область допустимых значений.

Проверим, входят ли в область допустимых значений .

. При - это неравенство не выполняется, т. е.n = 2k + 1, значит не входят в область допустимых значений и не являются корнями уравнения.

Ответ: .

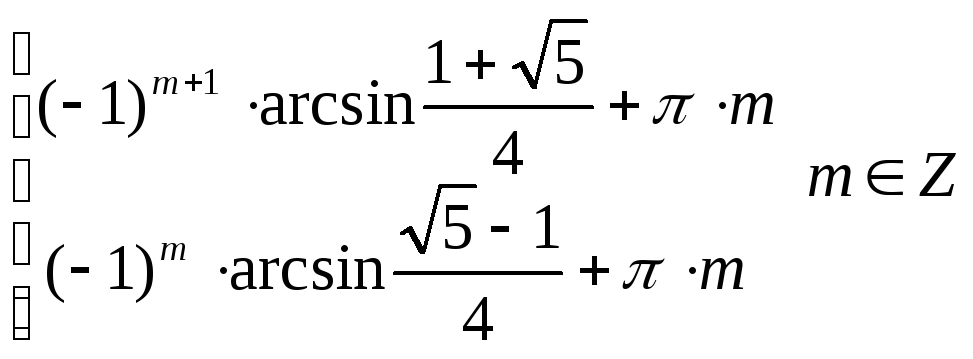Пример 46. Решите уравнение

Решение

Для решения уравнения применим формулу: , в которой положим, тогда,, получим уравнение:

.

Положим ,получим:

,

.

Ответ: .

Пример 47. Решите уравнение .

Решение

Преобразуем уравнение, применив формулу: , тогда получим уравнение:

.

Положим , получим:

,

,

.

Ответ: .

Пример 48. Решите уравнение .

Решение

Преобразуем уравнение, используя формулы:. Тогда уравнение примет вид:

Положим получим:.

Отсюда находим: .

Ответ: .

Пример 49. Решите уравнение.

Решение

Преобразуем уравнение, применяя тождество , получим уравнение:.

Пусть , получим:

,

.

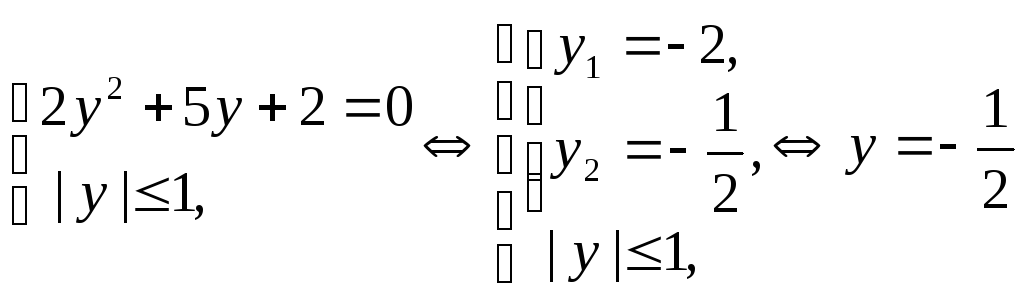Ответ:.

Пример 50. Решите уравнение .

Решение

Имеем уравнение, содержащее одинаковые функции с разными аргументами.

Преобразуем функцию к той же функции, но содержащей аргумент 2x.

Для этого применим формулу: . Подставляя в уравнение, получим:.

Положим , тогда получим систему:

.

Получим совокупность уравнений:

Ответ:

Пример 51. Решите уравнение .

Решение

Применим формулу , получим уравнение:.

Положим , получим смешанную систему:

,

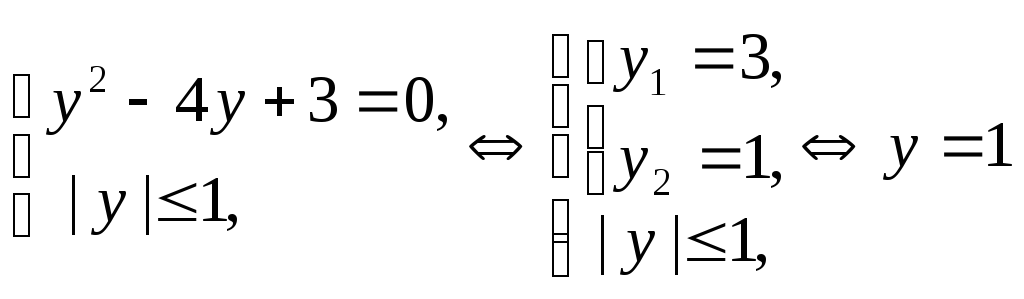Ответ: .