Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Брестский государственный технический университет

Предмет:

Высшая математика

Файл:

Контрольная работа №2 по высшей математике.pdf

Скачиваний:

Добавлен:

01.03.2016

Размер:

720.84 Кб

Скачать

☆

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

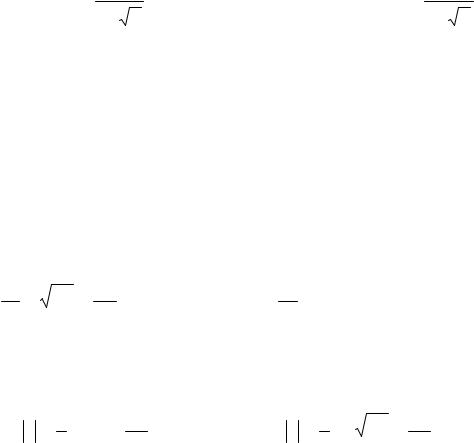
Вар.	26		27	28		29		30
an		3n2 − 2	3n + 2		5n +1		n	2n + 7
			6n n		3n		7 n (3n −1)	3n n
		n4 +1
x0	-2		-4	3		4		-3

Решение типового варианта контрольной работы № 2

Задание 1.

При нахождении неопределенных интегралов следует использовать таблицу интегралов основных элементарных функций, свойства интегралов и формулу интегрирования по частям. Найти неопределенные интегралы:

− 5 x3 −

5 dx +10

−

3 / 5 dx −

∫

18x5 +

dx =18

∫

−12∫x−4 dx =

x6 +10 ln

−

x3 / 5+1

−12

x−4+1

+ C =

− 4 +1

+10 ln x −

8 / 5

+ C = 3x

+10 ln x −

+ C.

′

ln x

u = ln x,

dx = x

2. ∫

dx =

du = (ln x)

= −

ln x −

dv =

x−5

= −

v = ∫

5x5

− 5

∫

ln x

∫

ln x

+ C

−

= −

5x5

= −

5x5

−

25x5

= −

5 ln x +1

+ C.

25x5

3. ∫(8x + 6) sin 3x dx =

u =8x + 6,

du = (8x + 6)′dx = 8 dx

dv = sin 3x dx,

v = ∫sin 3x dx = −

cos 3x

8x + 6

= −

cos 3x − ∫

−

cos 3x

8 dx = −

cos 3x +

∫cos 3x dx =

= −

8x + 6

cos 3x +

sin 3x + C.

4. ∫(3x − 4) e−x / 5 dx =

u = 3x − 4,

du = (3x − 4)′dx = 3dx

−

= −5e−x / 5

dv = e−x / 5 dx, v = ∫e

= −5e−x / 5 (3x − 4) − ∫(− 5e−x / 5 ) 3dx = −5 (3x − 4) e−x / 5 +

+15∫e−x / 5 dx = (−15x + 20) e−x / 5

− 75e−x / 5 + C = (−15x − 55) e−x / 5

+ C =

= −5(3x +11) e−x / 5

+ C.

5. ∫ln (x + 8) dx =

u = ln (x + 8),

du =

= x ln(x +

8) − ∫

dx =

x + 8

+ 8

dv = dx,

v = ∫dx = x

(x + 8) − 8

= x ln (x + 8) − ∫

dx = x ln (x + 8)

− ∫ 1 −

dx =

x + 8

= x ln (x + 8) − ∫dx + 8∫

= x ln (x + 8) − x + 8 ln (x + 8) + C =

x +

= (x + 8) ln (x + 8) − x + C,

x + 8 > 0.

Замечание

При

интегрировании

неправильных

алгебраических

дробей

вида

ax + b

надо

предварительно

cx + d

выделить целую и дробные части.

6x +15

(6x + 3) +12

3 (2x +1) +12

6. ∫

dx = ∫

= ∫

dx =

∫

dx =

2x +1

2x +

2x +1

12 dx

= ∫3dx + ∫

= 3x + 6 ln

2x +1

+ C.

2x +1

Задание 2. Пусть: a = 2; b = 5; c = 3; x0 = 2; y0 =1; l = 2; m = 3.

Тогда

z = 2x3 + 5x2 y + 3xy 2 − 4xy +15 y + 3, A (2;1), a = (2; 3).

1. Находим частные производные первого и второго порядка z = f (x, y). При дифференцировании функции z по х переменная у

временно считается постоянной; при дифференцировании z по у переменная х считается постоянной.

z′x = 6x2 +10xy + 3y 2 − 4 y;		z′y = 5x2 + 6xy − 4x +15;
′′	′′	′′

z xx =12x +10 y; zxy =10x + 6 y − 4; z yy = 6x.

Вычислим значения функции и ее производных в точке А

(2;1).

z( A) = 2 23 + 5 22 1 + 3 2 11 − 4 2 1 +15 1 + 3 =16 + 20 + 6 − 8 + +15 + 3 = 52,

z′x ( A) = (6x2 +10xy + 3y 2 − 4 y) = 6 22 +10 2 1 + 3 1 − 4 1 =

= 24 + 20 + 3 − 4 = 43,

z′y ( A) = (5x2 + 6xy − 4x +15) = 5 4 + 6 2 1 − 4 2 +15 = 20 +12 −

− 8 +15 = 39,

z′xx′ ( A) = (12x +10 y) A = 24 +10 = 34,

z′xy′ ( A) = (10x + 6 y − 4) A = 20 + 6 − 4 = 22, z′yy′ ( A) = (6x) A =12.

Эластичности функции z по переменным х и у в точке А равны:

Ex (z( A)) =	x	z′x	=		2		43 =1,65 ;
	z				52
				A

E y (z( A)) =	y	z′y				1	39 = 0,75.
				=
	z				52
				A

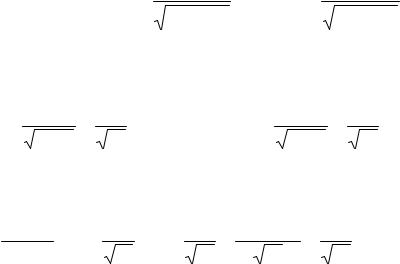
2.Составим матрицу Гессе функции z в точке А и вычислим

ееопределитель

z′′			( A)	z′′		( A)		34	22	,
H ( A) =	xx				xy		=			,
	′′				′′			22
zxy ( A)				z yy ( A)				22	12
det H ( A) =		34		22	= 34 12 − 222 = 408 − 484 = −76.
det H ( A) =		34		22	= 34 12 − 222 = 408 − 484 = −76.
		22		12

3. Градиент функции z в точке А – это вектор

grad z = (z x′( A) ; z y′( A)) = z x

′( A) i + z y′( A) j.

В данном случае grad z ( A) = 43 i + 39 j = (43; 39).

4. Производная функции z = f (x, y) в точке А по направлению

вектора a = (l ; m) вычисляется по формуле

∂ z ( A)

= z′x ( A) cosα + z′y ( A) cos β,

∂ a

где направляющие косинусы cosα и cos β вектора a

соответственно равны:

cosα =

; cos β =

l 2 + m2

Для вектора a = (2 ; 3) в силу предыдущих формул получим

cosα =

= 0,555;

cos β =

= 0,832.

4 + 9

4 +

Тогда

∂ z ( A)

= 43

+ 39

3 =

86 +117 =

203

= 56,302.

∂ a

Так как производная положительна, то в направлении вектора a , при прохождении через точку А функция z возрастает.

Задание 3.		a = 0,25; b = 0,10;	c = 0,40; p1 =13; p2 = 26.
1. Стоимость всего товара равна				P = p1 x + p2 y =13x + 26 y , а
затраты	на	производство	этих	товаров	составляют

C = 0,25x2 + 0,10xy + 0,40 y 2 . Следовательно, функция прибыли имеет вид П(x, y) = P − C =13x + 26 y − (0,25x2 + 0,10xy + 0,40 y 2 ).

Исследуем функцию прибыли на локальный экстремум. Находим частные производные П′x (x, y) и П′y (x, y) и

приравниваем их нулю. Получаем систему линейных уравнений

П′x (x, y) ≡13 − 0,5x − 0,1y = 0,П′y (x, y) ≡ 26 − 0,1x − 0,8 y = 0.

Решаем эту систему
0,5x + 0,11y =13,		5x + y =130,		y =130 −			5x,
	= 26.		= 260.				− 5x) = 260.
0,1x + 0,8 y		x + 8 y		x + 8 (130
− 39x = 260 − 8 130, 39x = 780, x = 20,						y = 30.
Точка	А (20;30) – стационарная точка функции П(x, y).
Покажем, что при х = 20, у = 30 прибыль будет максимальной.
Находим		′′		′′		= −0,1;	′′
		Пxx = −0,5;		Пxy			Пyy = −0,8. Составим
матрицу Гессе для функции П(x, y)					в точке А
		Пxx′′		Пxy′′		− 0,5	− 0,1
		H ( A) =	′′	′′		=		.
							− 0,8
			Пxy	Пyy		− 0,1
Так	как	det H ( A) = 0,5 0,8 − 0,12 = 0,40 − 0,01 = 0,39 > 0 и

элементы матрицы Н(А), стоящие на главной диагонали, отрицательны, то точка А является точкой максимума функции

П(x, y) .

Пmax (20 ; 30) =13 20 + 26 30 − (0,25 202 + 0,1 20 30 + 0,4 302 ) =

=260 + 780 − (100 + 60 + 360) = 520 (ден. ед.).

Таким образом, чтобы при заданных ценах р1 и р2 получить наибольшую прибыль, надо произвести 20 единиц товара первого вида и 30 единиц товара второго вида.

2. Предельная стоимость товара первого вида равна р1 = 13 (ден. ед.), а предельные издержки на его производство составляют Cx′ ( A) = 0,5 20 + 0,1 30 =10 + 3 =13 (ден. ед.).

Предельная стоимость товара второго вида р2 =26, а затраты на производство C′y ( A) = 0,1 20 + 0,8 30 = 2 + 24 = 26 (ден. ед.).

Таким образом, по двум видам товаров их предельная цена совпадает с предельными затратами на их производство.

Задание 4. Найти общее или частное решение дифференциальных уравнений.

Пример 1. Проинтегрировать ДУ

′

sin

x = y ln y

sin

= y ln y

sin

x dy = y ln y dx.

Разделим переменные и проинтегрируем обе части равенства

∫

= ∫

∫

d(ln y)

= ∫

sin 2

y ln y

sin 2 x

y ln y

ln y

sin 2

ln y

= −ctgx + C

общий интеграл

исходного

ДУ,

где

C − const.

Пример

Найти

частное

решение

ДУ

(2x +1) dy − ( y + 4) dx = 0, удовлетворяющее условию y (4) =11.

Разделяем переменные

d (2x +1)

(2x +1) dy = ( y + 4) dx

∫

d( y + 4)

∫

y +

2x +1

y + 4

2x +1

+ ln

0 ≠ C − const ln

y + 4

= ln C

2x +1 y + 4 = C 2x +1 y = C 2x +1 − 4

общее

решение данного уравнения.

Определим постоянную С так, чтобы выполнялось начальное условие y (4) =11.

11 = C 2 4 +1 − 4, 11 = 3C − 4, 3C =15, C = 5.				Получаем			частное
решение данного уравнения в виде y = 5 2x +1 − 4.
					y′ +	3y	2		− 4x,
Пример 3. Найти		частное	решение	ДУ			=
						x		x
удовлетворяющее начальному условию y(1) = 4.
Находим общее решение исходного уравнения с помощью
замены y = u (x) v (x), y	′	′	′
		= u (x) v (x) + u (x) v (x). Подставляем эту

замену в уравнение

′

+ u

′

3u v

− 4x,

u′ v + u v

′ +

− 4x.

Функции v (x)

и u (x) определяем из условий

v′

= 0,

′

− 4x.

u v =

v′ +

3 dx

= 0

= −

= −3 ln

= ln

v =

′ = 2x2 − 4x4 , du = (2x2 − 4x4 ) dx,

u′ v =

− 4x, u′

− 4x, u

u = ∫(2x2 − 4x4 ) dx =

3 −

+ C.

Общее решение ДУ имеет вид

y = u v, y =

−

+ C

y =

−

x2 ,

C − const.

Определим С из начального условия y (1) = 4.

4 = C +

−

, C = 4 −

60 −10 +12

Искомое частное решение имеет вид y =

−

x 2 .

15x3

Задание 5. Найти общее решение следующих ЛОДУ:

1) y′′ + y′ − 56 y = 0 ;

y′′+16 y′+ 64 y = 0.

2) y′′ −16 y′ + 68 y = 0 ;

Найти общее решение ЛНДУ:

4) y′′− 4 y′+3y = 5xe−x ,

6) y′′−6 y′+9 y = 4e3x ,

y′′ + 25y = cos 5x.

5) y′′− 4 y′+3y = (8x − 4) ex ,

7) y′′−6 y′+10 y =3cos x − 4sin x,

Решение. Пример1. y′′ + y′ − 56 y = 0.

С помощью замены

y = ekx

приходим к характеристическому

уравнению

k 2 + k − 56 = 0,

D =1 − 4 (−56) =1 + 224 = 225,

k =

−1 ±15

, k =

−1 −15

= −8,

−1 +15

= 7.

1,2

Общее решение ДУ есть:

y = C e−8x

+ C

e7 x , где C ,

− const.

Если

надо

выделить

частное решение,

удовлетворяющее

начальным условиям, например,

′

= −10, то находим

y (0) = 5; y (0)

y′(x) ,

y′(x) = −8C1e−8x + 7C2 e7 x .

Далее составляем систему уравнений для нахождения С1 и С2.

y (0) = 5,			C + C			= 5,	C		= 5 − C	,
′				1	2			2	1
y (0) = −10.			− 8C1 + 7C2 = −10.				−8C1 + 35 − 7C1 = −10.
C	= 5 − C		,	C1	= 3, C2 = 2.
2		1		C1	= 3, C2 = 2.
−15C1 = −45.

Частное решение имеет вид y = 3 e−8x + 2 e7 x .

Пример 2. y′′ −16 y′ + 68y = 0.

k 2 −16k + 68 = 0, (k − 8) 2 + 4 = 0, (k − 8) 2 = −4, k −8 = ± − 4 = ±2i, k1,2 = 8 ±2i, α = 8, β = 2.

Общее решение данного уравнения запишется в виде: y = C1e8x cos 2x + C2 e8x sin 2x, где C1 , C2 − const.

Пример 3. y′′ +16 y′ + 64 y = 0.

k 2 +16k + 64 = 0, (k + 8)	2 = 0, k = −8.
	1,2
Общее решение

y = C e−8x + C		2	xe−8x , где C , C	2	− const.
1			1
Пример	4.		y′′− 4 y′+3y =5xe−x. Общее решение исходного

линейного неоднородного дифференциального уравнения второго

порядка с			постоянными			коэффициентами имеет вид:
y =	y	(x) + y* (x),	где	y	(x) -	общее решение соответствующего

однородного решения, y* (x) - частное решение неоднородного.

		(x) = ? y′′ − 4 y′ + 3y = 0, k 2 − 4k + 3 = 0,
y		(x) = ? y′′ − 4 y′ + 3y = 0, k 2 − 4k + 3 = 0,
k = 4 ± 16 −12 =								4 ± 2 , k =1; k			2	= 3.
1,2				2				2		1	2
	(x) = C e x			2		e3x		2
				+ C			,	C , C		− const.
y				+ C	2		,	C , C	2	− const.
			1		2			1	2
y		*	(x) = ?, f (x) = 5x e−x , P (x) = 5x, α = −1, α ≠ k , α ≠ k										2	.
		*						1				1	2
			Будем	искать				y* (x)	в виде		y* (x) = (ax + b) e−x ,		где a и b –

неопределенные пока коэффициенты, подлежащие вычислению. Найдем

y*' (x) = a e−x + (ax + b) e−x (−1) = e−x (a − ax − b) ,

y*″(x) = −e−x (a − ax − b) +e−x (−a) = −e−x (a − ax − b + a) = = −e−x (2a − ax − b).

Подставим y* , y*′, y*″ в исходное уравнение

y*″ − 4 y*′ + 3y* = 5x e−x .

Получим

−e−x (2a − ax − b) − 4e−x (a − ax − b) + 3 e−x (ax + b) = 5xe−x .

Сокращаем на e−x и приводим подобные

−2a + ax + b − 4a + 4ax + 4b + 3ax + 3b = 5x,

8ax − 6a + 8b = 5x.

Приравниваем коэффициенты при одинаковых степенях х

			5
x	8a = 5,	a =		,
x	8a = 5,	a =	8	,
x			8		3		3	5		15
x	− 6a + 8b = 0.		6		3		3	5		15
		b =		a =		a =			=		.
		b =		a =		a =			=		.
			8		4		4	8		32
			8		4		4	8		32

		5		15		−x
Частное решение имеет вид	y* (x) =		x +		e		.
		8
				32


Общее решение исходного ДУ есть
			5		15
y (x) = C e x + C	2	e3x +		x +		e−x , C		, C	2	− const.
y (x) = C e x + C		e3x +		x +		e−x , C		, C		− const.
1		8			32		1
		8			32

Пример 5. y′′− 4 y′+3y = (8x − 4) ex. y = y (x) + y* (x).

y (x) = C1e x + C2 e3x , т.к. соответствующее однородное ДУ

осталось тем же.

Ищем частное решение y* (x) ; f (x) = (8x − 4) e x , P1 (x) = 8x − 4, α =1 = k1 , поэтому

y* (x) = x (ax + b) e x = (ax 2 + bx) e x ,

y*′(x) =(2ax + b) e x + (ax2 + bx) e x =e x (ax2 + 2ax + bx + b),

y*″(x) = e x (ax2 + 2ax + bx + b + 2ax + 2a + b) = e x (ax2 + 4ax + bx + 2a + 2b).

Подставим выражения для y* , y*′, y*″ в левую часть

исходного уравнения

e x (ax2 +4ax +bx +2a +2b) −4e x (ax 2 +2ax +bx +b) +3 (ax2 +bx) = = (8x −4) e x .

Сокращая на e x и приводя подобные, будем иметь

− 2x + a − b = 4x − 2.

Приравниваем коэффициенты при одинаковых степенях х

x	− 2a = 4,	a = −2,

x			= 0.
	a − b = −2.	b = a + 2

Частное решение y*(x) = −2x 2 ex.

Общее решение исходного уравнения имеет вид

y (x) = C e x + C	2	e3x − 2x2 e x ,	C , C	2	− const.
1	2		1	2

Пример 6. y′′ − 6 y′ + 9 y = 4e3x .

y = y (x) + y* (x). y (x) = ? y′′ − 6 y′ + 9 y = 0, k 2 − 6k + 9 = 0,

(k − 3) 2 = 0, k1,2 = 3 y (x) = C1e3x + C2 x e3x .

y* = ? f (x) = 4 e3x , P0 (x) = 4, α = 3 = k1 = k2

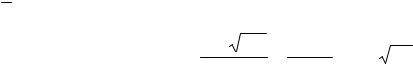
y* (x) = x2 a e3x .

y*′ = 2xa e3x + 3 ax2 e3x = a e3x = a e3x (2x + 3x2 ),

y*″ = a e3x (6x + 9x2 + 2 + 6x) = a e3x (9x2 +12x + 2),

y*″ − 6 y*′ + 9 y* = 4 e3x ,

a e3x (9x2 +12x + 2) − 6 a e3x (2x + 3x2 ) + 9 a e3x x2 = 4e3x .

Сокращая на e3x

и приводя подобные, получим 2a = 4, a = 2.

Следовательно,

(x) = 2x2 e3x ,

y (x) =e3x (C

+ C

x + 2x2 ),

C , C

− const.

Пример 7. y′′ − 6 y′ +10 y = 3 cos x − 4 sin x.

y =

(x) + y* (x).

y (x) = ? y′′ − 6 y′ +10 y = 0, k 2 − 6k +10 = 0,

D = 36 − 40 = −4,

= 6 ± − 4 = 6 ± 2i , i =

−1 − мнимаяединица.

1,2

k1,2 = 3 ± i, α = 3,

β =1.

(x) = C e3x cos x + C

e3x sin x,

C , C

− const.

y* (x) = ? f (x) = 3 cos x − 4 sin x y* (x) = a cos x + b sin x, a и b – пока неопределенные числа.

y*′(x) = −a sin x + b cos x, y*″(x) = −a cos x − b sin x.

y*″ − 6 y*′ +10 y* = 3 cos x − 4 sin x,

− a cos x − b sin x + 6 a sin x − 6b cos x +10a cos x +10b sin x = 3 cos x − 4 sin x.

Приравниваем коэффициенты при cos x и sin x .

cos x

− a − 6b +10a = 3,

9a −

6b = 3,

3a − 2b =1,

sin x

− b + 6a +10b = −4.

6a + 9b = −4.

a =

1 + 2b

+ 2b

1 + 2b

a =

1 + 2b

+ 9b

= −4.

+ 4b + 9b = −4.

13b = −6.

a =

1 −

b = −

Частное решение

y* (x) =

cos x −

sin x.

Общее решение данного уравнения имеет вид

y = C e3x cos x + C

e3x sin x +

cos x −

sin x,

C , C

− const.

Пример 8.

y′′ + 25y = cos 5x.

y =

(x) + y* (x).

(x) = ?

y′′ + 25 y = 0, k 2 + 25 = 0,

k 2 = −25,

k1,2

= ±

− 25 = ±5i ; α = 0,

β = 5.

(x) = C1 cos 5x + C2 sin 5x,

C1 , C2 − const.

y* (x) = ?

f (x) =1 cos 5x + 0 sin 5x y* = x(a cos 5x + b sin 5x),

а и b – const

y*′ = (a cos 5x + b sin x) + 5x (−a sin 5x + b cos 5x),

y*″ = 5 (−a sin 5x + b cos 5x) + 5 (−a sin 5x + b cos 5x) + 25x (−a cos 5x −.

− b sin 5x).

y*″ подставляем в исходное уравнение

Выражения для y* ,

y*″ + 25 y* = cos 5x.

10 (−a sin 5x + b cos 5x) − 25x (a cos 5x + b sin 5x) + 25x (a cos 5x + b sin 5x) = = cos 5x.

10 (−a sin 5x + b cos 5x) = cos 5x.

Приравниваем коэффициенты при sin 5x и cos 5x.

cos 5x	10b =1,	b = 0,1,

sin 5x
	−10a = 0.	a = 0.

Частное решение y* (x) = 0,1x sin 5x.
Общее	решение
y (x) = C1 cos 5x + C2 sin 5x + 0,1x sin 5x,	C1 , C2 − const.

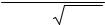
Задание 6.

∞

Примеры. Исследовать сходимость числовых рядов ∑un :

n=1

а) un =

; б)

;

в)

un =

7 n +1

;

(n2 +1) n!

(n + 3) ln 4 (n +

(n + 3) n

+ 3

г)

3n2

+ 4n + 7

n5 + 6

∞

а)

∑

+...

2 +

n=1 (n

1) n!

2 1

5 2

10 6

Здесь

;

(n2 +1)

3n+1

un+1

((n +1) 2 +1)

2 + 2n + 2)

(n +

(n +1)! (n

1)!

n! = (эн-факториал) = 1 2 3 ... n ;

(n +1)!= n!(n +1).

Здесь удобно применить признак Д'Аламбера.

lim

un+1

= lim

3n+1 (n2 +1) n!

= lim

3 (n2 +1)

n→∞

n→∞ (n2 + 2n + 2) n!(n +1) 3n

n→∞ (n

2 + 2n + 2) (n +1)

= 3 lim

= 3 0 = 0 <1,

n→∞

1 +

значит данный ряд сходится.

∞

б) ∑

+ ...

n=1 (n +1) ln 4 (n +

1) 2 ln 4

2 3 ln 4

3 4 ln 4 4

Нетрудно проверить, что в примерах б)-г) признак Д'Аламбера

ответа

не

дает,

поскольку

un =

(n +1) ln

(n +1)

un+1

(n + 2) ln 4

(n + 2)

lim

n+1

= lim

(n +1) ln 4

(n +1)

=1.

(n + 2)

n→∞

n→∞ (n + 2) ln 4

В данном случае применим интегральный признак Коши. Составим несобственный интеграл, соответствующий ряду

f (n) =	1	, 1 ≤ n < +∞;	f (x) =	1	, 1 ≤ x < +∞.
	(n +1) ln 4 (n +1)			(x +1) ln 4 (x +1)

∞

ln (x +1) = t

d(ln(x +1)) = dt

∫ f (x) dx = ∫

dx = ∫

d( ln(x +1))

(x +1) ln 4

(x +1)

1 ln 4 (x +1)

x =1 t = ln 2

x = ∞ t = ∞

+∞ dt

−4

t −3

= ∫

lim

∫t

= lim

−

3 N

3 +

3 ln

ln 2 t

N →∞ ln 2

N →∞

− 3

ln 2

N →∞

= 0 +

=1,001 (равен конечному числу).

3 ln 3

Так как несобственный интеграл сходится, то сходится и числовой ряд.

∞

7n +1

в) ∑

n=1 (n

+ 3)

n + 3

Признак Д’Аламбера ответа не дает, т.к.

u n =

7n +1

u n+1 =

7 (n +1)+1

7 n + 8

(n + 3) 3

(n + 4) 3

(n + 4) 32

u n+1

(7n + 8) (n + 3) 32

(7n

+ 8)

+ 3

lim

= lim

lim

=1.

(n + 4) 3

n→∞ u n

n→∞

2 (7n +1)

n→∞ (7n +1)

+ 4

Несложно составить соответствующий несобственный интеграл

∞	7 x +1
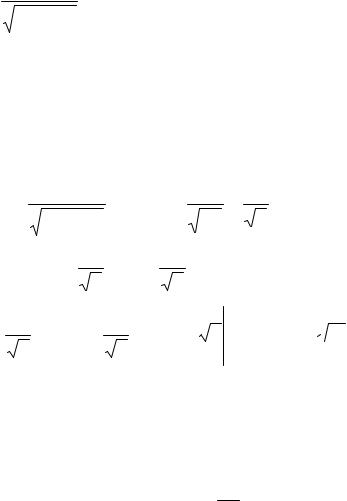
∫	7 x +1	dx .
1	(x + 3)	3

Сложнее вычислить этот интеграл или доказать его расходимость. Поэтому воспользуемся признаком сравнения.

Выпишем общий член un данного ряда и найдем общий член vn нового ряда из условия их эквивалентности

un ~ vn при n → ∞, т.е.							lim	un
un ~ vn при n → ∞, т.е.							lim
un = 7n +1						n→∞ vn
un = 7n +1					vn = 7n =
		(n + 3)3					n3
∞		∞	7		∞	1
∑ vn =∑			7	= 7 ∑		1	,
n=1		n=1	n		n=1	n		N
∞	dx		N	dx				N
∞			N
∫		= lim	∫		= lim		2 x
1	x	N →∞ 1		x	N →∞			1

=1.

7n ,

= 2 lim ( N −1) = ∞

N →∞

несобственный интеграл расходится, значит расходятся и сравниваемые ряды.

∞	3n	2	+ 4n + 7
г) ∑				.

n=1		n5 + 6

Сравним его с рядом ∑∞ 1 , который сходится как обобщенный

n=1 n3

гармонический ряд с p = 3 >1.

un =

3n2

+ 4n + 7

vn =

lim

= lim

(3n2 + 4n +

7) n3

5 + 6

n5 + 6

n→∞ vn

n→∞

3 +

= lim

= 3.

n→∞

1 +

Отсюда следует, что оба ряда ведут себя одинаково, т.е.

сходятся.

Задание 7.

а) an =	5n + 2				, x0 = 4.
а) an =	(n + 3) 7 n				, x0 = 4.
	(n + 3) 7 n
б) an =	4n2	−1	, x0			= −6.
б) an =	n4	+ 3	, x0			= −6.
	n4	+ 3
Решение.
а) Дан степенной ряд
				∞		∞	5n + 2
				∑ an (x − x0 ) n = ∑			5n + 2	(x − 4) n .
				∑ an (x − x0 ) n = ∑			(n + 3) 7 n	(x − 4) n .
(15)				n=1		n=1	(n + 3) 7 n
(15)

Найдем интервал его абсолютной сходимости. Для этого применим к ряду из модулей признак Д'Аламбера

un (x)

5n + 2

x − 4

n ,

un+1

(x)

5n + 7

x − 4

n+1

(n + 3) 7 n

(n + 4) 7 n+1

lim

un+1 (x)

= lim

(5n + 7)

x − 4

n+1 (n + 3) 7 n

x − 4

un (x)

n→∞

n→∞ (n + 4) 7 n+1 (5n + 2)

x − 4

5n2

× lim

(5n + 7)(n + 3)

x − 4

lim

x − 4

n→∞ (n + 4)(5n + 2)

n→∞ 5n2

Если

x − 4

< 7 − 7 < x − 4 < 7

− 3 < x <11, то ряд

(15) сходится абсолютно.

Если

x − 4

> 7 т.е.

x − 4 > 7,

x >11,

x − 4 < −7.

x < −3,

т.е. x (−∞;−3) (11; + ∞),

то ряд (15) расходится.

Если

x − 4

= 7 x = 4 ± 7, то

признак Д'Аламбера

ответа не дает.

расходится

абс. сходится

расходится

поведение ряда

-3

Исследуем поведение ряда (15) на концах интервала сходимости, т.е. при x = −3 и x =11.

∞

5n + 2

∞

5n + 2

x = −3.

∑ (−1) n

= ∑ (−1) n un , un

n + 3

n=1

n + 3

5n + 2

Так как lim un = lim

= 5 ≠ 0, то ряд расходится.

n→∞

n + 3

∞

5n + 2

∞

(5n + 2) 7

∞

5n + 2

x =11. ∑

(11 − 4) n = ∑

= ∑

(n + 3) 7 n

n + 3

n=1

ряд расходящийся, т.к. его общий член не стремится к нулю при n → ∞ (не выполняется необходимый признак сходимости ряда). Таким образом, областью сходимости степенного ряда (15) является интервал − 3 < x <11.

∞

−1

( x + 6) n .

б)

Рассматриваем степенной ряд вида∑

(16)

n=1

n4 + 3

Составляем ряд из модулей и применяем признак Д'Аламбера

∞

−1

n ,

∑

x + 6

n=1

n4 + 3

n+1 (n4 + 3)

(4 (n +1) 2 −1)

x + 6

lim

un +1

= lim

x + 6

n→∞

n→∞ ((n +1) 4 + 3) (n4 −1)

x + 6

× lim

4n2 n4

x + 6

n→∞ n4

4n2

Если

x + 6

<1 −1 < x + 6 <1 − 7 < x < −5,

то

ряд (16)

сходится абсолютно.
Если	x + 6	>1, т.е. x (−∞;−7) (−5 ; + ∞) , то ряд (16) расходится.
Если	x + 6	>1, т.е. x (−∞;−7) (−5 ; + ∞) , то ряд (16) расходится.
При x = −7 и x = −5 нужно дополнительное исследование.					2
		∞	(−1) n	4n	2	−1
1)		x = −7. ∑		4n		−1	,
1)		x = −7. ∑					,
(17)		n=1		n4 + 3
(17)

	∞	4n	2	−1
2)	x = −5. ∑				.

	n=1	n4 + 3

(18)

Очевидно, что ряд (18) сходится по признаку сравнения с рядом

∞

−1

(4n

−1) n

∑

, т.к.

lim

= lim

= 4.

n4 + 3

n=1

n→∞ n4 + 3 n2

n→∞

Значит, ряд (17) сходится абсолютно. Следовательно, областью сходимости степенного ряда (16) является отрезок x [−7 ; − 5].

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
01.03.201683.76 Кб66вышка(Rutegs).docx
#
01.03.2016702.19 Кб55вышка.docx
#
01.03.20161.77 Mб124Вышмат. Часть 1. Первый семестр. БрГТУ.pdf
#
01.03.2016605.31 Кб102Контрольная работа по математике №2.pdf
#
01.03.2016706.61 Кб148Контрольная работа №1 по высшей математике.pdf
#
01.03.2016720.84 Кб81Контрольная работа №2 по высшей математике.pdf
#
01.03.2016944.4 Кб81Контрольная работа №3 по высшей математике.pdf
#
01.03.2016900.21 Кб88Кр № 4 по математике (ФЗО техн).pdf
#
01.03.201612.6 Mб81математика.doc
#
01.03.2016566.31 Кб253Методичка по математике.1 курс.1 семестр.ФЭИС.pdf