
Сложная функция
-
Если задана некоторая функция
 ,
например,
,
например,
 ,
то это значит, что задано правило
соответствия
,
то это значит, что задано правило
соответствия
 .
Это правило предписывает произвести
над значением аргумента
.
Это правило предписывает произвести
над значением аргумента
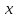 определенные действия, а именно, в нашем
случае, умножить его на 2 и затем к
произведению прибавить 1. В итоге
получаем определенное число -
соответствующее значение функции
определенные действия, а именно, в нашем
случае, умножить его на 2 и затем к
произведению прибавить 1. В итоге
получаем определенное число -
соответствующее значение функции
 .
Так, если
.
Так, если
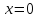 ,
то
,
то
 ,
а если
,
а если
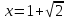 ,
то
,
то
 .
При
.
При
 получаем
получаем
 .
Областью определения функции является
числовое множество, в нашем примере –
это
.
Областью определения функции является
числовое множество, в нашем примере –
это
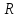 .
.
Рассмотрим
следующее выражение
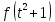 ,
в котором вместо аргумента данной
функции подставляется некоторая функция
от другого аргумента, а именно
,
в котором вместо аргумента данной
функции подставляется некоторая функция
от другого аргумента, а именно
 .
Можно записать это выражение в виде
.
Можно записать это выражение в виде
 .
Таким образом, мы имеем «функцию от
функции». Аргументом этой новой функции
является переменная
.
Таким образом, мы имеем «функцию от
функции». Аргументом этой новой функции
является переменная
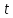 .
Значения функции
.
Значения функции
 ,
то есть
,
то есть
 ,
вычисляются следующим образом. Берется
значение аргумента
,
вычисляются следующим образом. Берется
значение аргумента ,
например, равное 2, и находится значение
функции
,
например, равное 2, и находится значение
функции
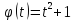 при
при
 .
Имеем
.
Имеем
 .
Далее вычисляем значение функции
.
Далее вычисляем значение функции
 при
при
 .
Получаем
.
Получаем
 .
Таким образом,
.
Таким образом,
 .
Для произвольного значения
.
Для произвольного значения
 имеем
имеем
 , то есть
, то есть
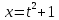 ,
значит
,
значит
 .
Поэтому формула функции
.
Поэтому формула функции
 имеет вид
имеет вид
 .
Отметим, что фактически в
.
Отметим, что фактически в были проделаны те действия, которые
предусматриваются правилом
были проделаны те действия, которые
предусматриваются правилом
 ,
однако эти действия были проделаны не
над аргументом х, а над выражением
,
однако эти действия были проделаны не
над аргументом х, а над выражением
 .
Функция
.
Функция
 получена в результате описанной операции
называется сложной. Термин «сложная»
используется здесь в смысле «составная»,
то есть сложная функция составлена из
других функций.
Дадим
точное определение сложной функции.
получена в результате описанной операции
называется сложной. Термин «сложная»
используется здесь в смысле «составная»,
то есть сложная функция составлена из
других функций.
Дадим
точное определение сложной функции.
Определение.
Пусть функция
 определена на множестве
определена на множестве
 ,
а функция
,
а функция
 – на множестве
– на множестве
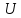 ,
причем множество значений функции
,
причем множество значений функции
 содержится в области определения функции
содержится в области определения функции
 .Поставим
в соответствие каждому числу
.Поставим
в соответствие каждому числу
 из
из
 число
число
 .
Тем самым на множестве
.
Тем самым на множестве
 будет задана функция
будет задана функция
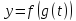 .
Эту функцию называют сложной функцией
или композицией функций
.
Эту функцию называют сложной функцией
или композицией функций
 и
и
 .
.
При
этом
 называют внешней, a
называют внешней, a
 — внутренней функцией композиции.
— внутренней функцией композиции.
Пример
1. Пусть
 .
Составьте сложную функцию
.
Составьте сложную функцию
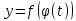 ,
если
,
если
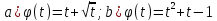 .
.
Решение.
Подставим вместо
 в формулу функции
в формулу функции
 ,
соответственно,
,
соответственно,
 и
и
 :
:
1. Получаем 1
 .
В итоге
.
В итоге
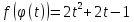 .
.
Пример
2. Даны две функции
 ,
соответственно,
,
соответственно,
 .
Найдите сложную функцию
.
Найдите сложную функцию

Решение.
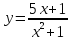 ,
,
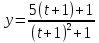 ,
,
 .
.
Рассмотрим
следующую задачу, в которой требуется
найти композицию функций
 и
и
 ,
причем первая функция – внешняя, а
вторая - внутренняя. Для удобства имеет
смысл ввести новые обозначения для
переменных второй функции, обозначив
ее аргумент буквой
,
причем первая функция – внешняя, а
вторая - внутренняя. Для удобства имеет
смысл ввести новые обозначения для
переменных второй функции, обозначив
ее аргумент буквой
 ,
а зависимую переменную – буквой
,
а зависимую переменную – буквой
 .
Имеем
.
Имеем
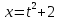 .
Важно понимать, что введение других
обозначений переменных никак не повлияло
на функцию. Записи
.
Важно понимать, что введение других
обозначений переменных никак не повлияло
на функцию. Записи
 и
и
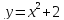 представляют одну и ту же функцию, с
областью определения
представляют одну и ту же функцию, с
областью определения
 ,
действие которой состоит в возведении
аргумента в квадрат и прибавлении числа
2.
,
действие которой состоит в возведении
аргумента в квадрат и прибавлении числа
2.
Композицией
функций
 и
и
 является функция
является функция
 .
В этом случае также ничего не мешает
обозначить другой буквой аргумент
сложной функции, а именно - буквой
.
В этом случае также ничего не мешает
обозначить другой буквой аргумент
сложной функции, а именно - буквой
 ,
то есть так, как обозначены аргументы
обеих функций в условии задачи. Таким
образом, получаем ответ:
,
то есть так, как обозначены аргументы
обеих функций в условии задачи. Таким
образом, получаем ответ:
 .
Заметим, что тот же результат можно
получить, если формально подставить в
формулу первой функции
.
Заметим, что тот же результат можно
получить, если формально подставить в
формулу первой функции
 вместо
вместо
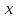 выражение
выражение
 .
На практике, конечно, можно пользоваться
этим приемом, при этом понимая
математический смысл произведенной
операции.
.
На практике, конечно, можно пользоваться
этим приемом, при этом понимая
математический смысл произведенной
операции.
Пример
3. Найдите сложную функцию, составленную
из функций
 и
и
 ,
где первая функция будет внешней, а
вторая - внутренней.
,
где первая функция будет внешней, а
вторая - внутренней.
Решение.
В первую функцию вместо
 подставим выражение
подставим выражение
 . В итоге получаем
. В итоге получаем
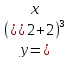 .
.
