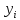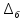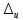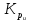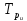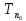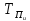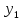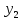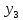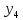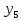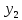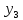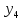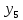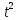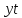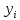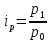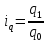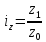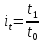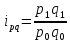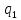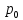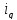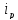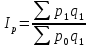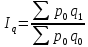Статистика.docx1789472326Статистика
.docxСписок литературы.
-
Н. В. Коник. Общая теория статистики: конспект лекций.
-
Годунов Б.А. Статистика, часть1, 2 (конспект лекций). 2008г..
-
Ефимова М.Р. и др. Общая теория статистики: Учебник. 1997 г.
-
Теория статистики./ Под ред. Р. А. Шмойловой. 1998г.
-
Практикум по теории статистики: Учебное пособие/ Под ред. Р. А. Шмойловой. 1999г.
Ряды динамики (продолжение).
Пример. Имеются условные данные о производстве телевизоров:
|
Годы |
2008 |
2009 |
2010 |
2011 |
|
Производство телевизоров, тыс. шт. |
886 |
953 |
995 |
996 |
Решение. Рассчитаем аналитические показатели динамики производства.
|
Годы |
|
Абсолютный прирост, тыс. шт. |
Коэффициент роста |
Темп роста, % |
Темп прироста, % |
Абсолютное значение 1% прироста (цеп.) |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
2008 |
886 |
– |
– |
1 |
– |
100 |
– |
– |
– |
– |
||||
|
2009 |
953 |
67 |
67 |
1,076 |
1,076 |
107,6 |
107,6 |
7,6 |
7,6 |
8,86 |
||||
|
2010 |
995 |
109 |
42 |
1,123 |
1,044 |
112,3 |
104,4 |
12,3 |
4,4 |
9,53 |
||||
|
2011 |
996 |
110 |
1 |
1,124 |
1,001 |
112,4 |
100,1 |
12,4 |
0,1 |
9,95 |
||||
|
Итого |
3830 |
|
|
|
|
|
|
|
|
|
||||
Средний уровень ряда (интервальный с равными интервалами):
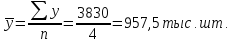
Таким
образом, среднегодовое производство
телевизоров за 2008-2011 гг. составит
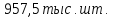
Средний
абсолютный прирост:
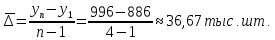 Таким образом, за 2008-2011 гг. производство
телевизоров в среднем росло на
Таким образом, за 2008-2011 гг. производство
телевизоров в среднем росло на
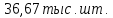 в год.
в год.
Средний
коэффициент роста:
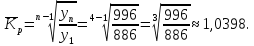
Средний
темп роста:
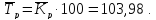
Средний
темп прироста:
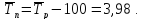 Таким образом, за 2008-2011 гг. производство
телевизоров в среднем росло на
Таким образом, за 2008-2011 гг. производство
телевизоров в среднем росло на
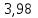 в год.
в год.
Пример. Имеются данные о стоимости основных средств предприятия на начало каждого квартала года: на 01.01.2011 г. – 14 млн. руб.; на 01.04. – 15 млн. руб.; на 01.07. – 17 млн. руб.; на 01.10. – 15 млн. руб.; на 01.01.2012 г. – 18 млн. руб. Какова средняя стоимость основных средств за 2011 год?
Решение. Моментный ряд с равными интервалами.
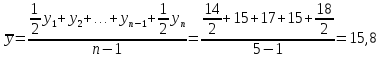 млн.
руб.
млн.
руб.
Одной из задач, возникающих при анализе рядов динамики, является установление закономерности изменения уровней изучаемого показателя во времени. Выявление основной тенденции развития (тренда) называется в статистике также выравниванием временного ряда.
Выявление тренда может быть произведено 3 методами:
-
укрупнение интервалов;
-
скользящая средняя;
-
аналитическое выравнивание.
При
аналитическом выравнивании находят
уравнение, выражающее закономерность
изменения явления как функцию времени
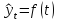 .
.
Виды трендовых моделей, наиболее часто используемые для аналитического выравнивания:
-
Линейная функция:
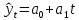 ;
; -
Парабола второго порядка:
 ;
; -
Показательная функция:
 ;
; -
Гиперболическая функция:
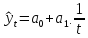 …
…
Рассмотрим
технику выравнивания ряда динамики по
прямой линии. Уравнение тренда будет
иметь вид:
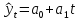 .
Система нормальных уравнений для
нахождения параметров уравнения имеет
вид:
.
Система нормальных уравнений для
нахождения параметров уравнения имеет
вид:
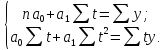
Вычислительный
процесс нахождения параметров уравнения
может быть значительно упрощен, если
ввести обозначения показателей времени
с помощью натуральных чисел так, чтобы
их была равна нулю
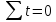 .
Так, если количество уровней в ряду
динамики нечетное, то временные даты
обозначаются так:
.
Так, если количество уровней в ряду
динамики нечетное, то временные даты
обозначаются так:
Таблица 3
|
Временные даты (периоды) |
Январь |
Февраль |
Март |
Апрель |
Май |
|
Уровни ряда динамики |
|
|
|
|
|
|
Обозначения временных дат (t) |
-2 |
-1 |
0 |
+1 |
+2 |
Если же количество уровней в ряду динамики четно, то обозначения временных дат (t) принимают следующий вид:
Таблица 4
|
Временные даты (периоды) |
Январь |
Февраль |
Март |
Апрель |
Май |
Июнь |
|
Уровни ряда динамики |
|
|
|
|
|
|
|
Обозначения временных дат (t) |
-5 |
-3 |
-1 |
+1 |
+3 |
+5 |
В
этом случае система нормальных уравнений
при выравнивании по прямой примет вид
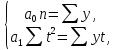 откуда
откуда
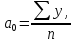 ;
;
 .
.
Пример. Имеются условные данные по одному из городов:
|
Годы |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
|
Численность населения, тыс. чел. |
50 |
52 |
54 |
55 |
52 |
55 |
Найти линию тренда. Определить численность населения в 2015 г. (прогноз).
Решение.
Предположим, что численность населения
изменяется по прямой
 .
.
|
Годы |
|
|
|
|
|
2008 |
50 |
-5 |
25 |
-250 |
|
2009 |
52 |
-3 |
9 |
-156 |
|
2010 |
54 |
-1 |
1 |
-54 |
|
2011 |
55 |
+1 |
1 |
55 |
|
2012 |
52 |
+3 |
9 |
156 |
|
2013 |
55 |
+5 |
25 |
275 |
|
Итого |
318 |
0 |
70 |
26 |
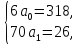 откуда
откуда
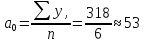 ;
;
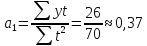 .
Уравнение тренда численности населения
примет вид:
.
Уравнение тренда численности населения
примет вид:
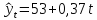 .
.
Для
2015 г.
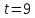 ,
следовательно численность населения
будет
,
следовательно численность населения
будет
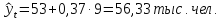
|
Годы |
|
Скользящая сумма 3-х членов |
Скользящая средняя 3-х членов |
|
2008 |
50 |
- |
- |
|
2009 |
52 |
156 |
52,00 |
|
2010 |
54 |
161 |
53,67 |
|
2011 |
55 |
161 |
53,67 |
|
2012 |
52 |
162 |
54,00 |
|
2013 |
55 |
- |
- |
Пример. По данным предыдущей задачи осуществить сглаживание ряда методом трехлетней скользящей средней.
В одной системе координат изобразить эмпирическую, сглаженную линии, а также линию тренда.
По
полученной модели тренда для каждого
периода (каждой даты) определяются
теоретические уровни тренда (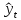 )
и стандартная ошибка аппроксимация
(среднее квадратическое отклонение
тренда) по формуле
)
и стандартная ошибка аппроксимация
(среднее квадратическое отклонение
тренда) по формуле
 ,
где y и
,
где y и
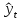 – соответственно фактические и расчетные
значения уровней динамического ряда;
n – число уровней ряда; m – число параметров
в уравнении тренда.
– соответственно фактические и расчетные
значения уровней динамического ряда;
n – число уровней ряда; m – число параметров
в уравнении тренда.
Нахождение по имеющимся данным за определенный период времени некоторых недостающих значений приказа внутри этого периода называется интерполяцией, за пределами анализируемого периода экстраполяцией.
При
составлении прогнозов уровней
социально-экономических явлений обычно
оперируют интервальной оценкой,
рассчитывая доверительные интервалы
прогноза. Границы интервалов определяются
по формуле
 ,
где
,
где
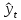 – точечный прогноз рассчитанный по
модели;
– точечный прогноз рассчитанный по
модели;
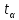 – коэффициент доверия по распределению
Стьюдента при уровне значимости
– коэффициент доверия по распределению
Стьюдента при уровне значимости
 .
.
Лекция 3.
Индексы.
Индекс – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Различия условий могут проявляться во времени, в пространстве и в выборе в качестве базы сравнения какого-либо условного уровня.
В
международной практике индексы принято
обозначать символами
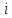 и
и
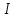 :
буквой
:
буквой
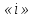 обозначаются индивидуальные индексы,
буквой
обозначаются индивидуальные индексы,
буквой
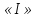 – общие индексы. Используются определенные
символы
для обозначения индексируемых показателей:
– общие индексы. Используются определенные
символы
для обозначения индексируемых показателей:
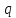 – количество
(объем) какого-либо товара в натуральном
выражении;
– количество
(объем) какого-либо товара в натуральном
выражении;
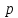 – цена
единицы товара;
– цена
единицы товара;
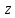 – себестоимость
единицы продукции;
– себестоимость
единицы продукции;
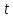 – затраты
времени на производство единицы
продукции;
– затраты
времени на производство единицы
продукции;
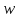 – выработка
продукции в стоимостном выражении на
одного рабочего или в единицу времени;
– выработка
продукции в стоимостном выражении на
одного рабочего или в единицу времени;
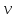 – выработка
продукции в натуральном выражении на
одного рабочего или в единицу времени;
– выработка
продукции в натуральном выражении на
одного рабочего или в единицу времени;
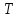 – общие
затраты времени (tq) или численность
рабочих;
– общие
затраты времени (tq) или численность
рабочих;
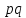 – стоимость
продукции или товарооборот;
– стоимость
продукции или товарооборот;
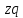 – издержки
производства.
– издержки
производства.
Индивидуальный индекс характеризует изменение во времени (или в пространстве) отдельных элементов той или иной совокупности.
Индивидуальные
индексы (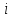 с подстрочным знаком индексируемого
признака:
с подстрочным знаком индексируемого
признака:

 )
вычисляются как отношение показателя
отчетного периода (со знаком 1) к
одноимённому показателю базисного (со
знаком 0)
)
вычисляются как отношение показателя
отчетного периода (со знаком 1) к
одноимённому показателю базисного (со
знаком 0)
|
|
– |
|
|
|
– |
|
|
|
– |
|
|
|
– |
|
|
|
– |
|
Индивидуальные
индексы повторяют связь признаков.
Например, признаки взаимосвязаны
равенством (количество) (цену)=(выручка),
тогда
(цену)=(выручка),
тогда
 .
.
|
№ п/п |
Товар |
Объем продаж, кг. |
Цена за 1 кг., ден. ед. |
Индивидуальные индексы |
||||||
|
Баз. период |
Отч. период |
Баз. период |
Отч. период |
объема продаж |
цен |
общей стоимости |
||||
|
|
|
|
|
|
|
|
||||
|
1 2 |
А Б |
10 15 |
12 13 |
100 150 |
150 200 |
1,2 0,9 |
1,5 1,33 |
1,8 1,2 |
||
Например,
для товара А индивидуальные индексы
получены так:
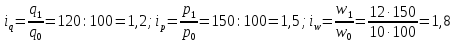 .
Для проверки вычислим
.
Для проверки вычислим
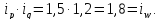
Таким образом, индексы увязаны в систему.
Замечание.
Индексы можно выражать в процентах.
Например, для товара А
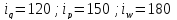 .
.
Выводы. В отчетном периоде по сравнению с базисным периодом:
объем продаж товара А увеличился на 20%, а цена за кг. увеличилась на 50%, при этом общая сумма продаж увеличилась на 80%;
объем товара Б уменьшился на 10%, а цена увеличилась на 33%, в результате общая сумма продаж возросла на 20%;
Сводный (агрегатный) индекс – это сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из непосредственно несоизмеримых элементов.
Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина), а другая остается неизменной (вес) индекса.
Индексируемая величина – признак, изменение которого изучается.
Вес индекса – величина, используемая для сравнения индексируемых величин.
К агрегатным индексам относятся:
|
|
сводный индекс товарооборота (показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным. Если из значения индекса вычесть 100 %, то разность покажет, на сколько процентов возросла (сократилась) стоимость продукции в текущий период по сравнению с базисным); |
|
|
сводный индекс цен (по методу Пааше) (показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен); |
|
|
сводный индекс физического объема продукции (по методу Ласпейреса) (показывает, во сколько раз возросла (сократилась) стоимость продукции из-за роста (снижения) объема ее производства; весом будет цена. Если из значения индекса вычесть 100 %, то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущий период по сравнению с базисным из-за роста (снижения) объема ее производства). |
Между рассчитанными индексами существует следующая взаимосвязь:
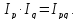
Пример.
Расчет общего индекса выручки:
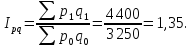
Вывод: выручка от реализации всех товаров в отчетном периоде по сравнению с базисным выросла на 35 %.
Определение общего индекса цен:
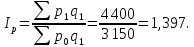
Вывод: в отчетном периоде по сравнению с базисным цены на товары выросли на 39,7 %.
Общий индекс физического объема товарооборота:
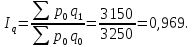
Вывод: в отчетном периоде по сравнению с базисным физический объем продаж снизился на 3,1 %.
Используя между показателями взаимосвязь, проверим правильность расчетов:
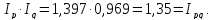
Аналогично рассмотренным индексам строятся и рассчитываются агрегатные индексы других взаимосвязанных экономических показателей.
Достоинством агрегатных индексов является то, что с их помощью можно определять не только относительные, но и абсолютные изменения явлений. К примеру, абсолютный прирост товарооборота (выручки) в целом определяется разностью между числителем и знаменателем индекса товарооборота (выручки):
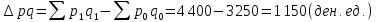
В том числе за счет изменения уровня цен:
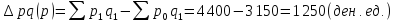
За счет изменения физического объема товарооборота:
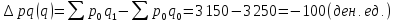
При этом общий прирост товарооборота представляет собой сумму приростов за счет изменения цен и за счет изменения объема продаж:


Вывод:
выручка от продажи товаров в отчетном
периоде по сравнению с базисным
увеличилась на 35%, что составило
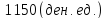 При этом за счет роста цен на товары на
39,7 % выручка возросла на
При этом за счет роста цен на товары на
39,7 % выручка возросла на
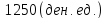 ,
хотя за счет снижения объемов продаж
на 3,1 % ее значение уменьшилось на
,
хотя за счет снижения объемов продаж
на 3,1 % ее значение уменьшилось на

В ряде случаев на практике вместо индексов в агрегатной форме удобно использовать средние арифметические и средние гармонические индексы.
Например,
нам известен товарооборот в текущем
периоде
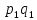 и индивидуальные индексы цен
и индивидуальные индексы цен
 .
Тогда сводный индекс цен
.
Тогда сводный индекс цен
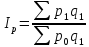 можно выразить в форме средней
гармонической из индивидуальных индексов
можно выразить в форме средней
гармонической из индивидуальных индексов
 ,
где
,
где
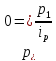 .
.
Если
известен товарооборот в базисном периоде
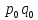 и индивидуальные индексы физического
объема
и индивидуальные индексы физического
объема
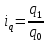 ,
то сводный индекс физического объема
товарооборота
,
то сводный индекс физического объема
товарооборота
 можно выразить в средней арифметической
форме, то есть
можно выразить в средней арифметической
форме, то есть
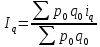 ,
где
,
где
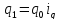 .
.