Аттестационная работа

Таким образом, уравнение плоскости запишется в виде:

Расстояние от точки до плоскости находится по формуле:

В нашем случае:

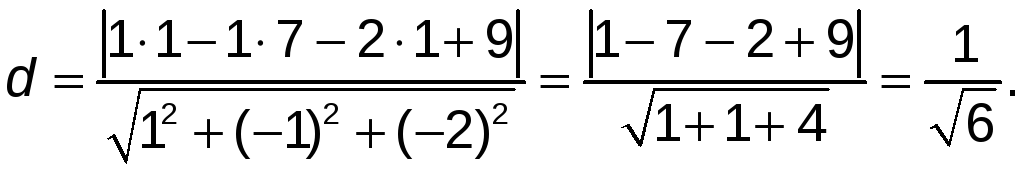
Ответ:

№10. Вычислить пределы:

а) .

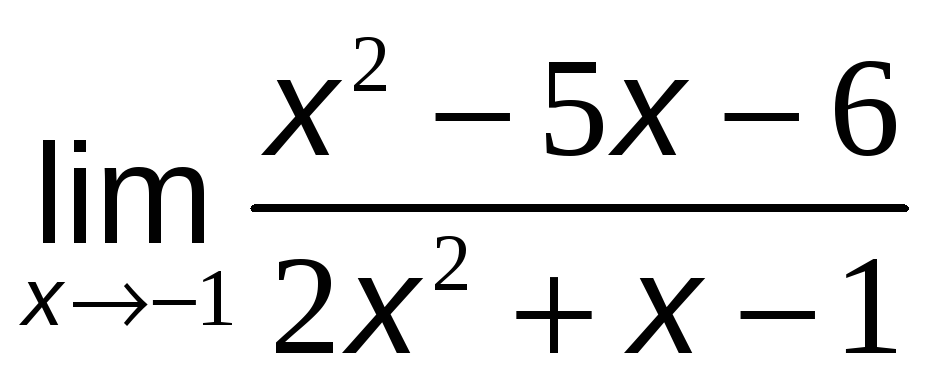Решение:

При числитель и знаменатель дроби обращаются в нуль, то есть мы имеем неопределённость вида . Разложим числитель и знаменатель на множители:

Квадратное уравнение имеет корни , . Значит, .

Квадратное уравнение имеет корни , . Значит, .

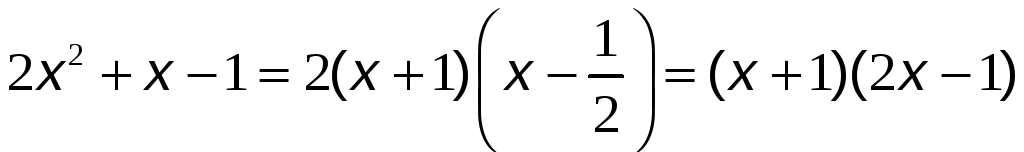Поэтому .

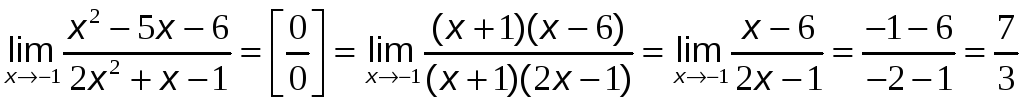Ответ:

б) .

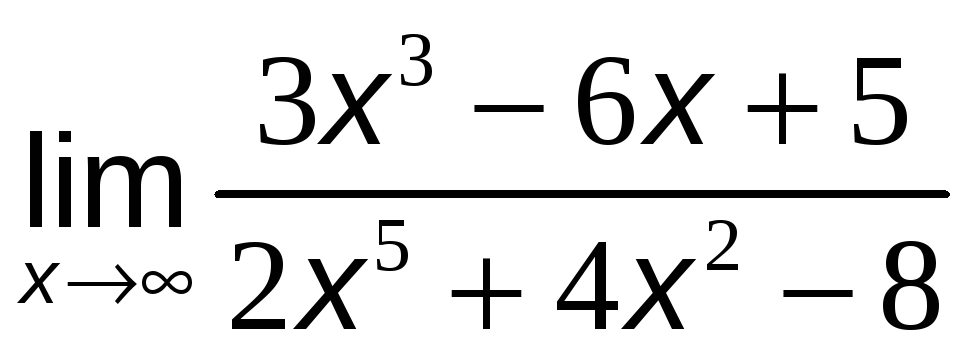Решение:

При числитель и знаменатель дроби также стремятся к бесконечности, то есть мы имеем неопределённость вида .

,

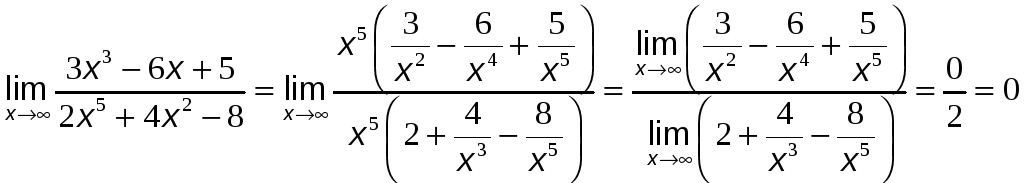так как частные стремятся к нулю при .

Ответ:

в) .

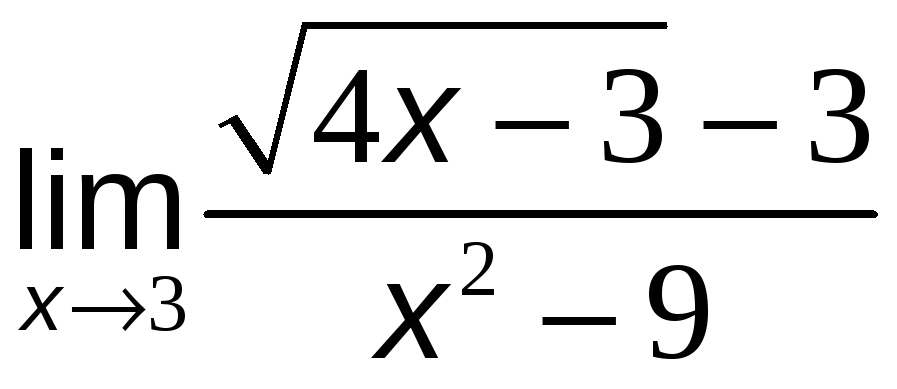Решение:

При числитель и знаменатель дроби обращаются в нуль, то есть мы имеем неопределённость вида . Для раскрытия этой неопределённости умножим числитель и знаменатель дроби на выражение, сопряжённое числителю:

.

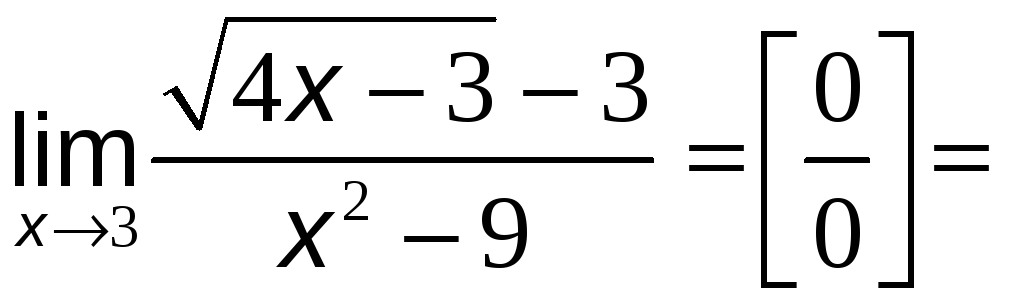
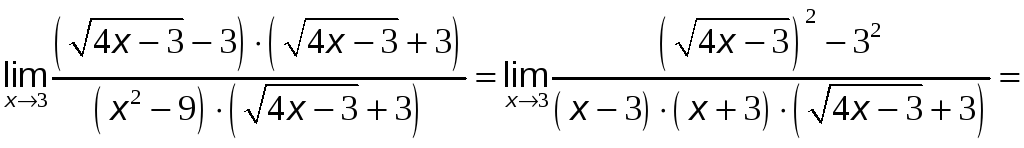
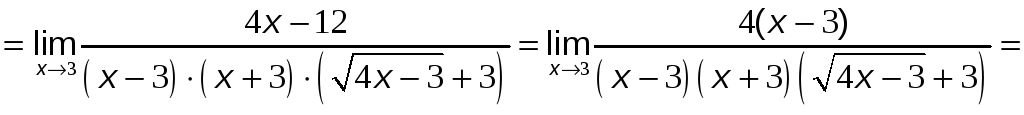
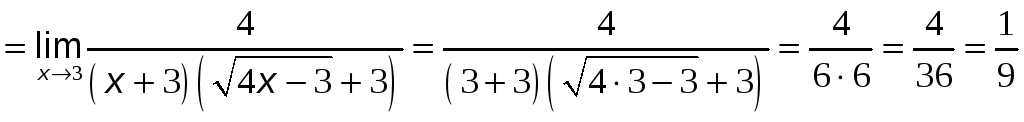Ответ: .

г) .

Решение:

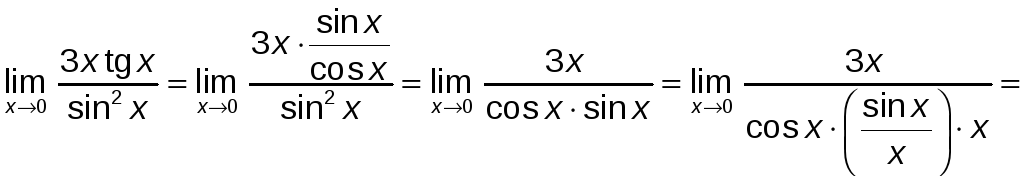
так как (первый замечательный предел), а .

Ответ: .

№11. Вычислить , используя эквивалентные бесконечно малые функции.

Решение:

так как , , при .

Ответ: .

№12. Исследовать функцию на непрерывность и построить её график.

Решение.

Функция определена и непрерывна на интервалах , где она задана непрерывными элементарными функциями. Следовательно, разрыв возможен только в точках и .

Для точки имеем:

, , . Так как , то функция в точке является непрерывной.

Для точки имеем:

, , , т.е. функция в точке имеет разрыв первого рода. При этом скачок функции в точке равен .

График функции имеет вид:

№13. Найти производную функций

а) .

Решение:

б) .

Решение:

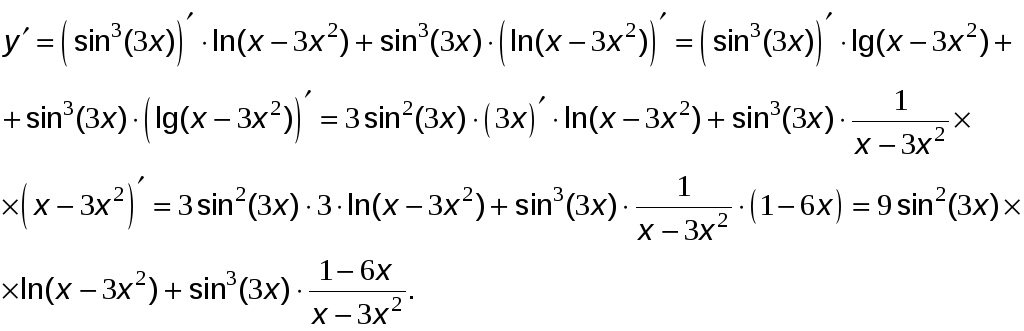
в) .

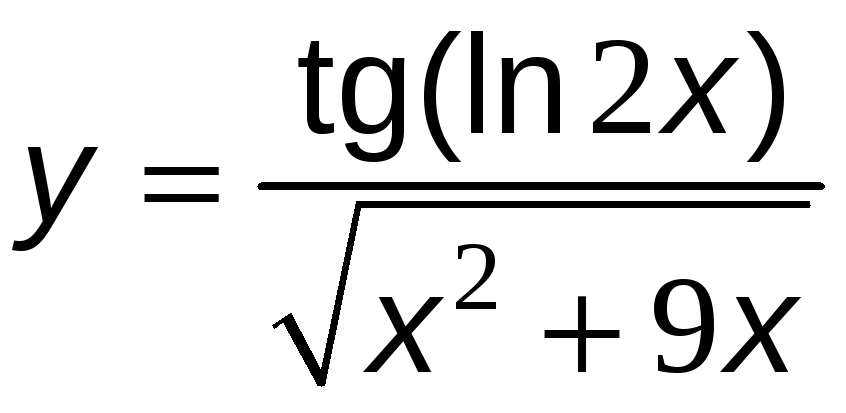Решение.

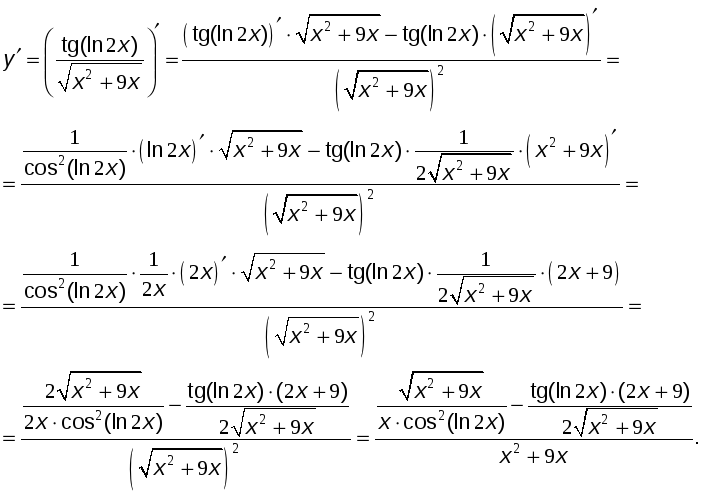
№14. Найти , используя правило Лопиталя.

Решение:

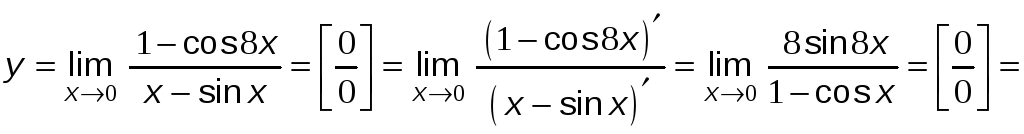
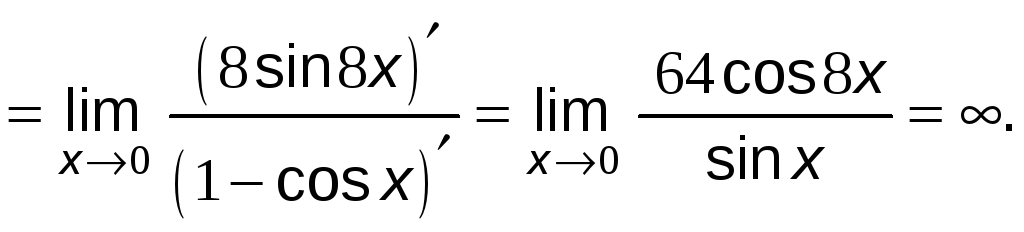
№15. Найти промежутки возрастания и убывания, точки максимума и минимума функции, промежутки вогнутости и выпуклости, точки перегиба графика функции .

Решение:

Находим критические точки функции из равенства :

.

– критические точки функции .

Эти точки разбивают область определения функции на промежутки , , . Определим знак производной на каждом их этих промежутков:

Т.о., функция возрастает на промежутках и и убывает на промежутке . При этом точка является точкой максимума функции, а точка – её точкой минимума.

Для определения промежутков выпуклости и вогнутости находим вторую производную и приравниваем её к нулю:

.

.

Т.о., точка графика с абсциссой является подозрительной на перегиб. Точка разбивает область определения функции на промежутки и . Определим знак второй производной на каждом их этих промежутков:

Т.о., график функции является выпуклым на промежутке и вогнутым на промежутке .

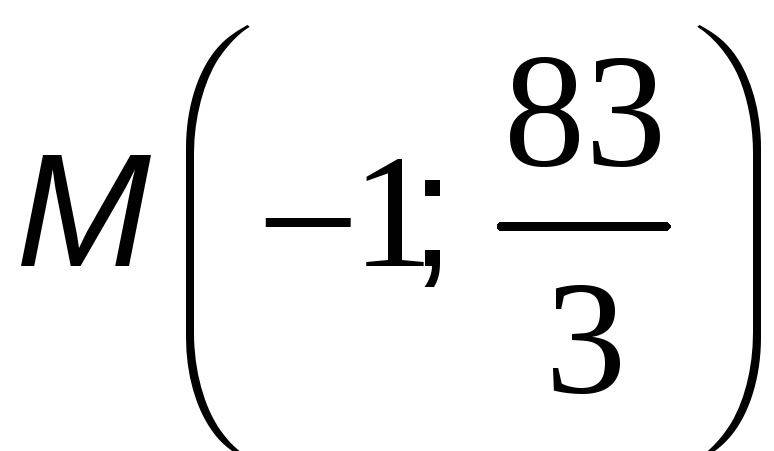Поскольку , то точка является точкой перегиба графика функции.