Типовой расчет (2): «Кинематика и динамика вращательного движения. Законы сохранения. Элементы механики колебательного движения» Задание для самостоятельной работы (2)
Диск массой m и
радиусом
вращается с угловой скоростью
.
В момент времени
к ободу диска прижимают тормозную
колодку с силой
,
направленной перпендикулярно оси
вращения. Коэффициент трения между
диском и колодкой равен
.
Сколько оборотов сделает диск до остановки, если вещество, из которого изготовлен диск, распределено по нему равномерно?
Найти работу сил трения от начала торможения до остановки диска в случае равномерного распределения массы по диску.
Определите число оборотов диска от начала торможения до остановки и работу сил трения за это время, если масса вещества диска распределена по закону:
,
а прижимающая сила зависит от времени
по закону:
,
где
,
и
— постоянные величины.
Однородный
стержень массой
и длиной
может вращаться без трения в вертикальной
плоскости вокруг оси, проходящей через
его конец. В другой конец вертикально
висящего стержня попадает летящий
горизонтально со скоростью
шарик
массой
и прилипает к нему.
Определить начальную угловую скорость и угол максимального отклонения стержня после попадания шарика.
Найти угол максимального отклонения стержня и выделившееся при ударе количество теплоты, если шарик попадает в стержень под углом
.
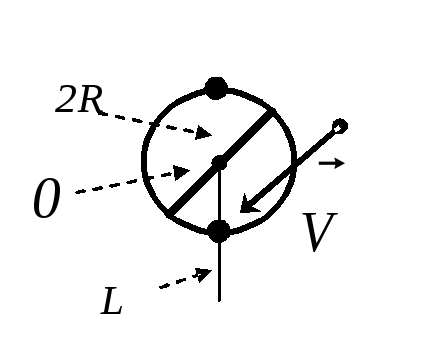
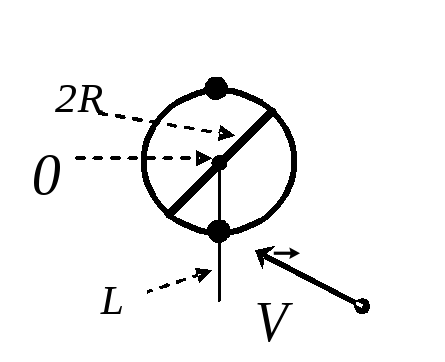
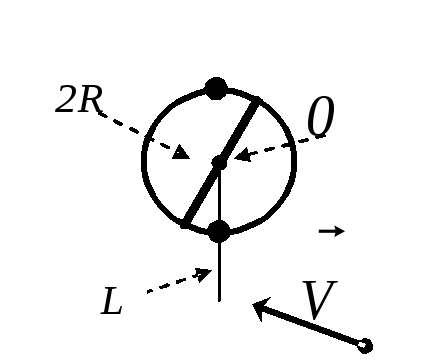
Механическая система состоит из
горизонтально расположенной оси в форме
цилиндра радиуса
и массой
,
двух стержней и тела массой
в виде обруча или дискарадиуса
,
прикрепленных к оси. К телу прикреплены
два шарика массой
.
Способ крепления элементов системы
указан в таблице вариантов
(2). Масса
и длина первого стержня
и
,
второго —
и
,
соответственно. В нижнем конце второго
стержня прикреплен шарик массой
.
В один из элементов системы попадает,
как показано в таблице вариантов
(2), шарик
массой
,
летящий со скоростью
,
направленной под углом
к горизонту и
прилипает к нему. Трением оси с креплением пренебречь.
Определить начальную угловую скорость системы после попадания шарика, угол максимального отклонения системы и выделившееся при ударе количество теплоты.
Определить период установившихся малых колебаний системы.
Варианты условий (2)
ТАБЛИЦА ИСХОДНЫХ ДАННЫХ (2)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер варианта N равен порядковому номеру студента в журнале группы. Число k задается для всей группы преподавателем, ведущим занятия. Размерности в таблице исходных данных и сами данные проставляются студентами самостоятельно, кроме случаев, указанных в таблице.
ТАБЛИЦА ВАРИАНТОВ (2)
|
N |
Система |
Шарик попадает в |
|
|
|
нижний
конец стержня длиной
|
|
|
|
нижний
конец стержня длиной
|
|
|
|
правый
конец стержня длиной
|
|
|
|
правый
конец стержня длиной
|
|
|
|
нижний
шарик массой
|
|
|
|
нижний
шарик массой
|
|
|
|
правый
конец стержня длиной
|
|
|
|
правый
конец стержня длиной
|
|
|
|
нижний
шарик массой
|
|
|
|
нижний
шарик массой
|
|
|
|
верхний
шарик массой
|
|
|
|
верхний
шарик массой
|
|
|
|
верхний
шарик массой
|
|
|
|
левый
конец стержня длиной
|
|
|
|
правый
конец стержня длиной
|
|
|
|
правый
конец стержня длиной
|
|
|
|
нижний
конец стержня длиной
|
|
|
|
нижний
конец стержня длиной
|
|
|
|
правый
конец стержня длиной
|
|
|
|
правый
конец стержня длиной
|
|
|
|
правый
шарик массой
|
|
|
|
правый
шарик массой
|
|
|
|
правый
конец стержня длиной
|
|
|
|
правый
конец стержня длиной
|
|
|
|
правый
шарик массой
|
|
|
|
правый
шарик массой
|
|
|
|
левый
шарик массой
|
|
|
|
левый
шарик массой
|
|
|
|
левый
конец стержня длиной
|
|
|
|
левый
конец стержня длиной
|
