Подбор площади сечения арматуры полки плиты

Рабочая высота сечения полки плиты равна , где с - величина защитного слоя бетона, . Тогда .

Определим граничное значение относительной высоты сжатой зоны бетона:

, где предельное значение относительной деформации арматуры равно , относительная деформация бетона . Тогда относительная высота сечения бетона

Определим граничное значение коэффициента ,

где ; .

.

Расчет арматуры для усилия М₁

Определим значение .

Т. о. .

Определим коэффициент , где

Требуемая площадь сечения арматуры

Минимальная площадь , где - минимальный процент армирования, . Тогда . Учитывая , принимаем по сортаменту 5о4 шаг 200 с площадью .

Расчет арматуры для момента М₂

Определим значение .

Т. о. .

Определим коэффициент

Требуемая площадь сечения арматуры

Минимальная площадь равна . Учитывая , принимаем по сортаменту 5о3 шаг 200 с площадью .

2.4.4 Расчет поперечного ребра плиты Исходные данные

Поперечное ребро рассматривается как балка на двух свободных опорах с расчетным пролетом, равным расстоянию между осями продольных ребер (схема 11).

Поперечное ребро загружено постоянной и снеговой нагрузкой по следующей схеме:

Грузовой площадью для поперечного ребра будет являться расстояние равное расстоянию между поперечными ребрами (т.е. 1500мм). Расчетным сечением ребра является тавровое сечение с шириной сжатой полки (схема 12).

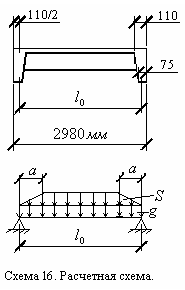
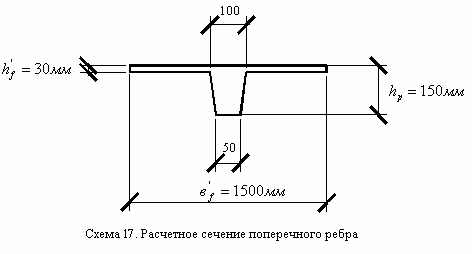
Рис.2.16. Расчётная схема плиты и размеры поперечного ребра плиты.

Нагрузки, действующие на поперечное ребро:

1. Постоянная нагрузка, передаваемая плитой: ;

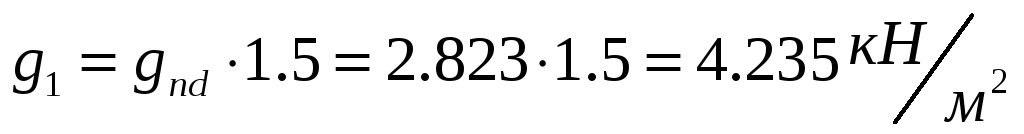2. От собственного веса поперечного ребра: 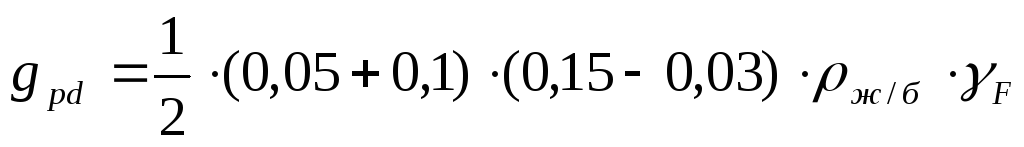, где . Тогда .

Тогда полная постоянная нагрузка равна .

3. Снеговая нагрузка, действующая на поперечное ребро:

Изгибающий момент будет равен , где

.

Поперечная сила на опоре равна:

.

Расчет прочности нормальных сечений

Поперечное ребро армируем одним плоским каркасом с однорядным расположением рабочей арматуры. Принимаем величину защитного слоя бетона , где в I приближении принимаем , а . Тогда . Принимаем .

Определяем рабочую высоту сечения бетона .

В I приближении принимаем, что относительная высота сжатой зоны равна , где . .

При полученной высоте сжатой зоны определяем область деформирования и коэффициент : , значит 2 область деформирования.

Проверим условие положения нейтральной оси относительно высоты сечения ребра.

,

где

. Следовательно, нейтральная ось проходит в пределах полки, и сечение рассматриваем как прямоугольное с шириной .

, где .

Тогда . По определим .

Определим .

,

Определим .

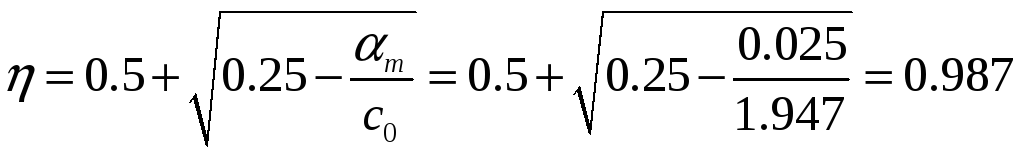, где - средняя ширина ребра.

Учитывая , по сортаменту принимаем 2о16 S500 с площадью .

Расчет прочности наклонных сечений

Проверим условие необходимости поперечного армирования:

,

где ,

где ;

. Принимаем ;

.

.

где

и следовательно, поперечное армирование устанавливается конструктивно. Принимаем арматуру о4 класса S500 с шагом 100 мм.

2.4.5 Расчет продольного ребра плиты Исходные данные

Расчетная схема продольного ребра плиты представляет собой решетку на двух опорах, загруженную постоянной и переменной снеговой нагрузкой. Принимаем, что

расстояние осей опор находиться не ближе 6 см от торца плиты, определяем расчетный пролет плиты: (схема 13).

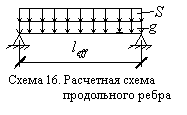
Для определения погонной нагрузки на продольное ребро плиты равномерно распределенную нагрузку с учетом веса плиты и снеговую нагрузку умножаем на грузовую площадь, равную шагу плит, т.е. на 3м. Тогда нагрузка равна:

1. Расчетная нагрузка при основной комбинации

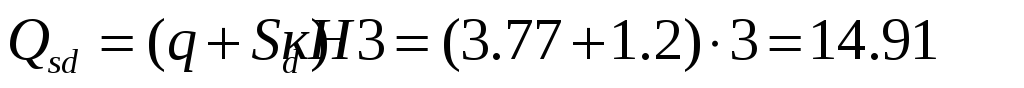
2. Нормативное значение нагрузок

- для редкой комбинации

Тогда соответствующий изгибающий момент будет равен:

.

Поперечная сила от расчетной нагрузки будет равна:

.

Определим площадь сечения рабочей арматуры в продольном ребре. Действительное П-образное сечение плиты приводим к эквивалентному тавровому сечению, при этом в качестве полки таврового сечения будет выступать полка плиты, в качестве ребра таврового сечения будет выступать удвоенное среднее значение размера продольного ребра плиты, т.е. , .