
Кинематика
.docКИНЕМАТИКА
Задача К22. Диск радиусом R вращается вокруг своего неподвижного вертикального диаметра с угловой скоростью ω. По ободу этого диска перемещается точка М так, что угол О1ОМ= φ = f(t). Определить абсолютную скорость и абсолютное ускорение точки М в момент t1 (рис. 52, табл. 61, где φ – в рад, R – в см , t1- сек, ω - в с-2).
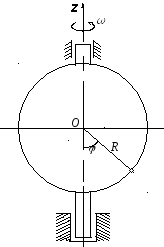
Рис. 52
Таблица 61
|
№ |
|
|
|
|
|
1 |
|
15 |
|
2.5 |
|
2 |
|
21 |
|
1 |
|
3 |
|
10 |
|
3 |
|
4 |
|
15 |
|
2.5 |
|
5 |
|
18 |
|
2 |
|
6 |
|
20 |
|
3.5 |
|
7 |
|
12 |
|
2 |
|
8 |
|
18 |
|
1.5 |
|
9 |
|
18 |
|
3 |
|
10 |
|
12 |
|
2 |
З адача
К23.
Прямоугольный треугольник ABC
с гипотенузой BC=a
и углом α вращается вокруг катета AC
с угловой скоростью ω. По его гипотенузе
перемещается точка М по закону СМ= s
= f(t).
Определить абсолютную скорость и
абсолютное ускорение точки М в момент
t1
(рис. 53, табл. 62, длины заданы в см, t1-
сек, ω - в с-1).
адача
К23.
Прямоугольный треугольник ABC
с гипотенузой BC=a
и углом α вращается вокруг катета AC
с угловой скоростью ω. По его гипотенузе
перемещается точка М по закону СМ= s
= f(t).
Определить абсолютную скорость и
абсолютное ускорение точки М в момент
t1
(рис. 53, табл. 62, длины заданы в см, t1-
сек, ω - в с-1).
Рис. 53
Таблица 62
|
№ |
|
|
|
|
|
|
1 |
48 |
60° |
|
|
2 |
|
2 |
50 |
45° |
|
|
2 |
|
3 |
36 |
60° |
|
|
2.5 |
|
4 |
60 |
30° |
|
|
5 |
|
5 |
60 |
45° |
|
|
3 |
|
6 |
80 |
45° |
|
|
2 |
|
7 |
80 |
45° |
|
|
2.5 |
|
8 |
40 |
30° |
|
|
1.5 |
|
9 |
24 |
30° |
|
|
3 |
|
10 |
98 |
60° |
|
|
3 |
Задача К24.
В кулисном механизме при качании
кривошипа ОС вокруг неподвижной оси О,
перпендикулярной к плоскости чертежа,
ползун А, перемещаясь вдоль кривошипа
ОС, приводит в движение стержень АВ,
соединенный с ползуном А шарнирно и
перемещающийся в наклонных направляющих,
образующих с осью Ох угол
![]() .
Определить скорость и ускорение стержня
АВ в момент t1,
если заданы угол поворота кривошипа φ,
отсчитываемый от положительного
направления оси Ох как функция времени
t, и расстояние h (рис. 54, табл. 63, где h —
в см, φ — в рад).
.
Определить скорость и ускорение стержня
АВ в момент t1,
если заданы угол поворота кривошипа φ,
отсчитываемый от положительного
направления оси Ох как функция времени
t, и расстояние h (рис. 54, табл. 63, где h —
в см, φ — в рад).


Рис. 54
Таблица 63
|
№ |
|
|
|
|
|
1 |
20 |
0° |
|
4 |
|
2 |
30 |
60° |
|
|
|
3 |
16 |
90° |
|
1 |
|
4 |
40 |
45° |
|
|
|
5 |
24 |
45° |
|
3 |
|
6 |
20 |
60° |
|
|
|
7 |
24 |
30° |
|
|
|
8 |
30 |
90° |
|
|
|
9 |
28 |
0° |
|
1.5 |
|
10 |
18 |
90° |
|
3.5 |
Задача К25. Кран вращается вокруг вертикальной оси по закону φ= f1(t). Крановая тележка перемещается по закону s = f2 (t). Определить абсолютную скорость и абсолютное ускорение тележки в момент t1 (рис. 55, табл. 64, где φ — в рад, a t — в сек).


![]()
Таблица 64
|
№ |
|
|
|
|
1 |
|
|
3 |
|
2 |
|
|
2 |
|
3 |
|
|
2 |
|
4 |
|
|
2 |
|
5 |
|
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
3 |
|
10 |
|
|
3 |
Задача К26.
Прямоугольник ABCD вращается вокруг оси
Oz по закону φ= f1(t).
По его диагонали АС перемещается точка
М по закону AM=s = f2(t).
Определить абсолютную скорость и
абсолютное ускорение точки М в момент
t1
сек, если диагональ АС составляет с осью
вращения угол
![]() (рис. 56, табл. 65, где s
– в см, а угол φ- в рад).
(рис. 56, табл. 65, где s
– в см, а угол φ- в рад).


![]()
Таблица 65
|
№ |
|
|
|
|
|
1 |
|
|
2 |
45° |
|
2 |
|
|
3 |
30° |
|
3 |
|
|
3 |
30° |
|
4 |
|
|
4 |
60° |
|
5 |
|
|
2 |
45° |
|
6 |
|
|
5 |
60° |
|
7 |
|
|
4 |
30° |
|
8 |
|
|
3 |
45° |
|
9 |
|
|
2 |
60° |
|
10 |
|
|
1.5 |
45° |
Задача К27.
Диск вращается вокруг своего горизонтального
диаметра с угловой скоростью ω. По его
диаметру, наклоненному к оси вращения
под углом
![]() ,
перемещается точка М по закону OM = s=f
(t). Определить абсолютную скорость и
абсолютное ускорение точки М в момент
t1
(рис. 57, табл. 66,
где s — в см, ω — в с-1,
t — в сек).
,
перемещается точка М по закону OM = s=f
(t). Определить абсолютную скорость и
абсолютное ускорение точки М в момент
t1
(рис. 57, табл. 66,
где s — в см, ω — в с-1,
t — в сек).
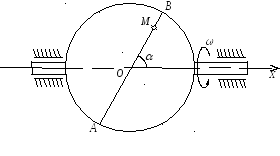
Рис. 57
Таблица 66
|
№ |
|
|
|
|
|
1 |
|
45° |
|
1 |
|
2 |
|
60° |
|
1 |
|
3 |
|
30° |
|
2 |
|
4 |
|
45° |
|
2.5 |
|
5 |
|
30° |
|
2 |
|
6 |
|
90° |
|
0.75 |
|
7 |
|
45° |
|
0.5 |
|
8 |
|
90° |
|
0.75 |
|
9 |
|
60° |
|
3 |
|
10 |
|
30° |
|
3 |
Задача К28.
Точка М движется по образующей конуса
по закону s = OM=f1(t).
Конус вращается вокруг своей оси с
угловой скоростью ω = f2(t).
Определить абсолютную скорость и
абсолютное ускорение точки М в момент
t1,
если угол МОА =
![]() (рис. 58, табл. 67;
s задано в см, t — в сек, ω — в с-1).
(рис. 58, табл. 67;
s задано в см, t — в сек, ω — в с-1).
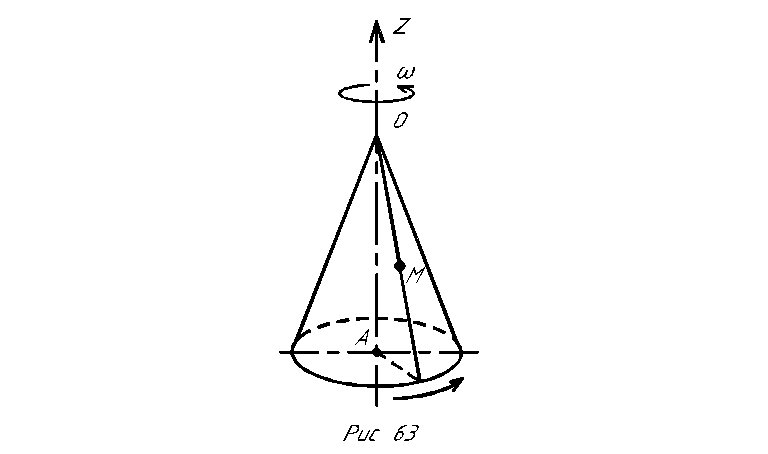

![]()
Таблица 67
|
№ |
|
|
|
|
|
1 |
|
|
30° |
1.5 |
|
2 |
|
|
45° |
2 |
|
3 |
|
|
60° |
2.5 |
|
4 |
|
|
30° |
2.5 |
|
5 |
|
|
45° |
2.5 |
|
6 |
|
|
60° |
2 |
|
7 |
|
|
30° |
3 |
|
8 |
|
|
45° |
4 |
|
9 |
|
|
45° |
4 |
|
10 |
|
|
60° |
3 |
