Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

TeorVer / Лекция 8. Распределения непрерывных случайных величин

.pdf

Скачиваний:

Добавлен:

01.03.2016

Размер:

383.82 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Лекция 8

РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

ЦЕЛЬ ЛЕКЦИИ: определить функции плотности и числовые характеристики случайных величин, имеющих равномерное, показательное, нормальное и гамма-распределение.

Равномерное распределение

Непрерывная случайная величина X имеет равномерное распреде-

ление на участке от		a	до	b , если ее плотность распределения	f (x) на
этом участке постоянна:
		1	, x	(a,b);
f (x)					(4.24)
	b	a
	0, x		(a,b).

В дальнейшем для непрерывных случайных величин выражение для плотности f (x) записывается только для тех участков, где она отлична от нуля:

f (x) b a , a x b .

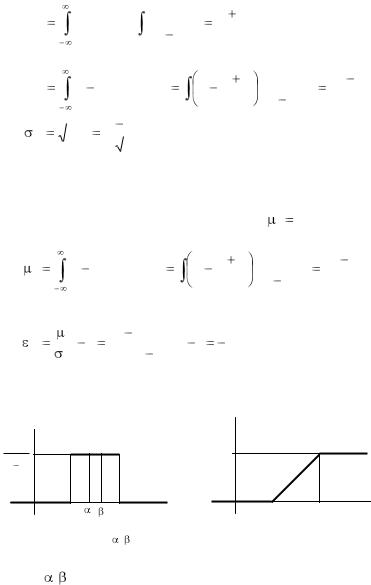
Значения f (x) в крайних точках a и b промежутка (a,b) не указываются, так как вероятность попадания в любую из этих точек равна

нулю. Кривая

распределения приведена

f ( x)

на рис. 4.19. Иногда это распределение

называют прямоугольным. Математиче-

ское ожидание случайной величины X

равно середине участка (a,b) :

a b

Рис. 4.19. Кривая равномерного

распределения

Этот же результат можно получить, вычисляя интеграл вида

mX xf (x)dx

x	1		dx	a b	.
x			dx		.
	b	a		2

Дисперсия и среднее квадратичное отклонение равны:

DX	(x mX )2 f (x)dx	b	x	a b 2	1		dx	(b a)2	;
				2	b			12
		a				a

				b	a	.
X	D	X

			2		3

Моды равномерное распределение не имеет. Медиана равна математическому ожиданию, так как равномерное распределение симметрично относительно математического ожидания. Из этого же свойства следует,

что третий центральный момент тоже равен нулю (	3	0 ).
	3

Для определения эксцесса вычислим четвертый центральный момент:

	(x mX )4 f (x)dx				b	x	a b 4	1		dx	(b a)4	.
4	(x mX )4 f (x)dx					x	2	b		dx	80	.
					a		2	b	a		80
					a
Таким образом, эксцесс случайной величины X равен
	4	3	(b a)4	(12)2		3	1,2 .
	4
X	4		80(b	a)4
X

	X

Следовало ожидать, что эксцесс этой случайной величины будет отрицательным.

	f ( x)			F ( x)
				F ( x)
	1			1
				1
b	a
	a	b	x	a	b	x
	Рис. 4.20. Вероятность попада-			Рис. 4.21. Функция распределения
	ния на участок (	,	)

Вычислить вероятность попадания случайной величины X на любую часть ( , ) участка (a,b) можно путем геометрических представлений (см. рис. 4.20):

}

Функция

распределения F (x) является функцией,

линейно взра-

стающей от нуля до единицы,

при изменении аргумента от a до b . При

любом x функция распределения равна площади,

ограниченной кривой

распределения и лежащей левее точки x (см. рис. 4.20).

0, x

x a

F (x)

f (x)dx

dx, a x b

, a x b .

a b

b a

1, x

Моделью равномерного распределения является гармоническое ко-

лебание со случайной начальной фазой

x(t)

cos(

0 ) ,

где 0 – частота, а начальная фаза

0 является непрерывной случайной

величиной с равномерным законом распределения:

f ( 0 )

, 0

2 .

Показательное распределение

Непрерывная случайная величина X имеет показательное (экспоненциальное) распределение, если ее плотность распределения имеет вид

	f (x)	e	x , x 0	,
	f (x)	0, x		,
		0, x	0
или
	f (x)	e	x , (x 0) ,			(4.25)
где	0 – единственный параметр распределения.
	Функция распределения:
			x		x
		F (x)	f (x)dx		e xdx 1 e x , (x 0) .	(4.26)

f ( x)	F ( x)
	F ( x)

		1

				x					x
	0			x				0	x
	0							0

Рис. 4.22. Плотность распределения							Рис. 4.23. Функция распределения
Математическое ожидание показательного распределения:
mX		xf (x)dx	x e	x	dx	1	.		(4.27)
mX		xf (x)dx	x e		dx		.		(4.27)
		0	0
При интегрировании по частям необходимо учесть, что при x									e x

стремится к нулю быстрее, чем возрастает любая степень x .

Выражение (4.27) показывает, что математическое ожидание случайной величины, имеющей показательное распределение, обратно его пара-

метру . При этом параметр			имеет размерность,					обратную размерно-
сти случайной величины X .
Дисперсия и среднее квадратичное отклонение:
DX	2 mX2	x2	e x dx	1	1					1
				1	1		, X		DX	1	. (4.28)

				2		2
		0

Среднее квадратичное отклонение случайной величины X , распределенной по показательному закону, равно ее математическому ожиданию.

Третий центральный момент:

			3
	x	1	e x dx	2	,
3	x		e x dx	3	,
	0

и соответственно коэффициент асимметрии

SX	3	2 .
	3

Следовало ожидать, что асимметрия показательного распределения будет положительной.

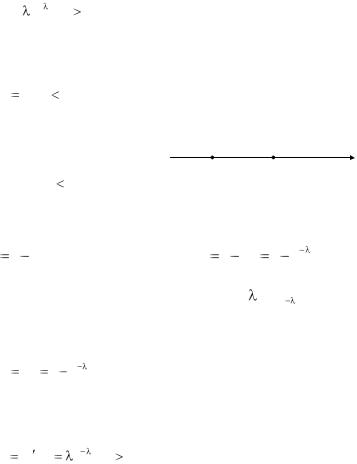
Показательное распределение связано с простейшим потоком событий. Покажем, что интервал времени между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром, равным интенсивности потока, т. е.

f (t) 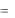e t , (t 0) .

Для этого найдем функцию распределения F(t) случайной величины T – интервала времени между соседними событиями в потоке:

F (t) P{T

t} .

На оси времени

отметим ин-

тервал T между соседними событиями

потока (см. рис. 4.24). Чтобы выполня-

лось неравенство

t ,

необходимо,

Рис. 4.24. Случайная величина Т

чтобы хотя бы одно событие потока

попало на участок длины t . Вероятность того, что это так,

R 1

P{ни одно событие не попало}

1 P

e t ,

(

t)0

где вероятность

для пуассоновского потока равна

откуда функция распределения будет иметь вид

F (t)

t ,

после дифференцирования которой получаем искомую плотность распределения

f (t) F (t)

e t , (t 0) .

Показательное распределение широко используется в теории марковских случайных процессов, теории массового обслуживания и теории надежности.

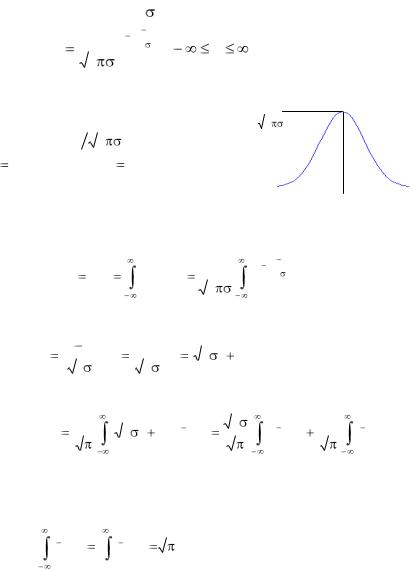
Нормальное распределение

Случайная величина X распределена по нормальному (гауссовому) закону с параметрами m и , если ее плотность распределения имеет вид

( x m)2

f (x)

(4.29)

Кривая

нормального

распределения

f ( x)

(см. рис. 4.25) имеет симметричный холмо-

образный вид. Максимальное значение кри-

вой,

равное

, достигается

при

m , т. е. мода M X

m .

Вычислим

основные

характеристики

случайной величины

X ,

распределенной

по

нормальному

закону.

Математическое

Рис. 4.25. Кривая нормального

ожидание

распределения

( x m)2

M [ X ]

xf (x)dx

dx .

Сделаем замену переменной интегрирования

; dt

; x

(4.30)

и получим

(

2 t m)e t

te t

e t

dt .

Первый из интегралов равен нулю, как интеграл в симметричных пределах от нечетной функции; второй – это известный интеграл Эйлера – Пуассона

e t 2 dt 2 e t 2 dt
e t 2 dt 2 e t 2 dt	.
0

Таким образом, математическое ожидание нормального распределения

mX m

(4.31)

совпадает с параметром распределения m . Иногда m называют центром рассеивания случайной величины X .

Дисперсия гауссовой случайной величины X

								1					( x m)2
D[ X ]		DX		(x mX )		2	f (x)dx	1		(x m)	2	e	2	2		dx .

								2
								2
Используя замену переменной (4.30), получаем
	2		2				интегриров ание по частям :
			2				интегриров ание по частям :

D				2t2e t dt					2						2


X					u t; du dt; dv 2te t ; v								e t
					u t; du dt; dv 2te t ; v								e t
	2			te t 2			e t 2 dt .

Первое слагаемое в фигурных скобках равно нулю, так как при t

e t 2	0 быстрее, чем возрастает t . Второе слагаемое равно
			.
	Таким образом, дисперсия
	DX	2 .	(4.32)

Значит, параметр распределения есть не что иное, как среднее квадратичное отклонение гауссовой случайной величины X :

X	DX	.
Размерности		и m совпадают с размерностью случайной величи-

ны X .

Положение кривой распределения и ее форма полностью определяются параметрами m и .

Вычислим моменты нормальной случайной величины X . Так, s -й центральный момент будет

			1				( x m) 2
(x m)	s	f (x)dx	1	(x m)	s	e	2	2	dx .

			2
			2

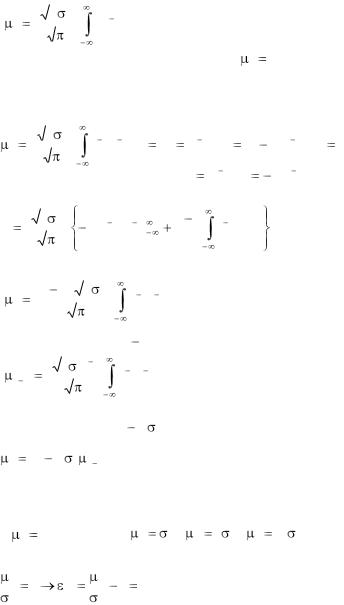
После замены переменой (4.30) получаем

					s
( 2			)		s									2
( 2			)							t se t				2	dt .
																										(4.33)

s
s
Естественно,			что при любом нечетном s																						s	0 , как интеграл в
																									s
симметричных пределах от нечетной функции. Для четных s :
				s																	интегриров ание по частям :
																					интегриров ание по частям :
( 2			)													2
( 2			)					t s 1te t								2	dt				u t s 1; du (s 1)t s 2dt;


s
s
																							dv	te t 2 ; v			1	e t 2
																							dv	te t 2 ; v		2		e t 2
																										2

	( 2 )s								1		e t 2 t s 1												s 1	t s 2et 2 dt .
	( 2 )s								1														s 1
									2														2


Первый член в фигурных скобках равен нулю, и поэтому получаем
		(s	1)(							)		s
							2					s									2
							2								t s 2e				t		2	dt .
																			t							(4.34)
s			2



Подставим в формулу (4.33) (s																	2)			вместо s :
(						)	s			2
			2				s			2								2
			2										t s				2e t		dt .

																										(4.35)
s 2

Сравнение выражений (4.35) и (4.34) показывает, что эти формулы различаются только множителем (s 1) 2 . Следовательно,

s (s 1) 2 s 2 .

Получено простое рекуррентное соотношение, позволяющее выражать центральные моменты более высоких порядков через центральные моменты более низких порядков. Если учесть, что для любой случайной

величины		0	1, то получаем			2	2 ;	4	3	4 ;	6	15 6 .
		0				2		4			6
Эксцесс нормального распределения равен нулю:
	4	3		4	3 0 .
	4	3	X	4	3 0 .
	4		X	4

Вероятность попадания случайной величины X на участок от 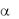до 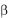определятся следующим образом:

( x m)2

замена :

}

f (x)dx

x m

t 2

2 dt

(4.36)

t 2

где (x)

2 dt

– функция Лапласа.

Вероятность того, что абсолютная величина отклонения гауссовой случайной величины X от своего математического ожидания m окажется меньше любого 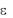0 , равна

	P{\| X		m \|	}		2 ( ) .			(4.37)
Если в выражении (4.36) положить								,	x и учесть, что
( )	12 ,	то получаем функцию распределения нормальной слу-
чайной величины X в виде
	F (x)		1		x	m	.		(4.38)
	F (x)	2					.		(4.38)
		2

Модель нормального распределения. Складывается большое количество независимых случайных величин X1 , X2 , , Xn

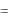X X i ,

i 1

при этом предполагается, что каждая из Xi сравнима по степени своего влияния на рассеивание суммарной случайной величины X . Закон рас-

F ( x)

1 / 2

Рис. 4.26. Функция распределения нормальной случайной величины

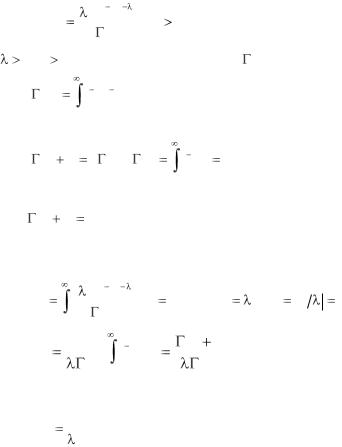
пределения суммы этих случайных величин (случайной величины X ) будет тем ближе к нормальному, чем больше число слагаемых n , вне зависимости от того, какие законы распределения имеют отдельные величи-

ны X1 , X2 , , Xn . Таково содержание центральной предельной теоремы теории вероятностей.

Гамма-распределение и распределение Эрланга

Неотрицательная случайная величина X имеет гамма-распределение, если ее плотность распределения выражается формулой

			k xk 1e	x
	fk (x)				, (x	0) ,	(4.39)
	fk (x)		(k)		, (x	0) ,	(4.39)
			(k)
где	0, k	0 – параметры распределения;					(k ) – гамма-функция
	(k)		e tt k 1dt ,				(4.40)
		0
которая обладает следующими свойствами:
	(k	1)	k (k);	(1)		e t dt 1.	(4.41)

Для целых неотрицательных k получаем

(k 1) k! .

Математическое ожидание случайной величины X , подчиняющейся гамма-распределению,

		x k xk	1e	x
mX		x k xk	1e		dx	замена : t		x, dx dt
mX	0	(k)			dx	замена : t		x, dx dt
		(k)

		1	e	ttk dt		(k 1)	.
			e	ttk dt			.
		(k)	0			(k)

Учитывая свойства (4.41), окончательно получаем

mX	k	.	(4.42)

1 / 21 2 > Следующая >>>

Соседние файлы в папке TeorVer

#
01.03.2016211.55 Кб101Лекция 3. Условная вероятность и независимость событий. Формула полной вероятности и теорема Байесса.pdf
#
01.03.2016324.38 Кб71Лекция 4. Независимые испытания.Формула Бернулли. Асимптотические формулы Муавра-Лапласа и Пуассона.pdf
#
01.03.2016301.94 Кб78Лекция 5. Случайные величины. Законы распределения случайных величин.pdf
#
01.03.2016265 Кб73Лекция 6. Числовые характеристики случайных величин.pdf
#
01.03.2016314.67 Кб61Лекция 7. Распределения дискретных случайных величин.pdf
#
01.03.2016383.82 Кб60Лекция 8. Распределения непрерывных случайных величин.pdf
#
01.03.2016357.14 Кб61Лекция 9. Закон распределения системы двух случайных величин.pdf
#
01.03.2016165.53 Кб47Литература и приложения.pdf
#
01.03.2016207.99 Кб43Титулный лист и предисловие.pdf
#
01.03.2016213.08 Кб43Учебная программа-временная.pdf