Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2014 КМ1 УСР3(пед)

.pdf

Скачиваний:

Добавлен:

01.03.2016

Размер:

229.96 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Для любой точки p l векторы N и (p - p0) взаимно перпендикулярны и, следовательно, имеет место условие (4).

Утверждение 5. В среде MathCAD общее уравнение прямой l (9)

может быть представлено в виде

NT ( p - p0 ) = 0 ,

(11)

где произвольная точка прямой p = (x, y) и точка p0

представлены в

каноническом виде (1), нормальный вектор N прямой

имеет вид (2).

Выражение (11) представляет модель общего уравнения прямой, если

она задана точкой p0

l и вектором нормали N.

Утверждение

вектором нормали N соотношением

6. Значение параметра D из общего уравнения прямой

(9) связано с точкой p0

l и

D = -NT p0 .

(12)

Обоснуйте утверждение

6. Для

этого

запишите

выражение

(11)

матричном

виде

(Nx

æ x - p

= 0

выполните

умножение

)ç

0 x

è y - p0 y ø

сопоставьте полученный результат с (9).

Рассмотрим

случай

3). Пусть

p = (x, y)

– произвольная

точка

плоскости, точка p

= (p0x, p0y),

V = (V

)

- направляющий вектор

прямой l.

Если

точка

то

векторы

(p - p0) коллинеарны и,

место условие (5). А именно,

следовательно, имеет

p - p0

= 0 .

(13)

Утверждение 7. В среде MathCAD общее уравнение прямой l (9)

может быть представлено в виде (13).

Выражение (13) представляет модель общего уравнения прямой, если

она задана точкой p0 l и направляющим вектором V.

Покажите, что выражение (13) представляет выражение (9). Для этого

запишите его в координатном виде	x - p0 x Vx			= 0 , выполните операцию
	x - p0 x Vx
	y - p	V	y
	0 y		y

вычисления определителя и преобразуйте результат.

Объясните, какие соглашения, принятые нами, не будут выполняться, если поменять местами столбцы определителя в модели (13).

Рассмотрим			случай				4). Пусть p = (x, y)		– произвольная точка
плоскости, точки a				l, b		l, a ≠ b.			(b - a) коллинеарны и,
Если точка		p l,			то		векторы (p - a) и

следовательно,	имеет место условие (5). А именно,
							p - a b - a	= 0,	(14)

									11

Утверждение 7. Уравнение (9), задающее прямую на плоскости, в среде MathCAD может быть представлено в виде (14).

В		Выражение (14) представляет модель общего уравнения прямой, если
В
она задана координатами двух различных точек, ей принадлежащих, т. е.
a		l, b	l, a ≠ b.
	координатном виде
				x - ax	bx - ax	= 0 .
				x - ax	bx - ax
				y - ay	by - ay

4.3.2 Параметрическое уравнение прямой

Рассмотрим задачу построения в среде MathCAD модели

параметрического уравнения прямой l
	p(t) = p0	+ Vt, t R ,			(15)

где точка p0 l и V - направляющий вектор прямой l.
Запишем уравнение (15) в координатной форме
	æ x(t)ö		æ p0 x ö	æVx ö	(16)
	ç	÷	= ç ÷	+ t ç ÷
	è y(t)ø		è p0 y ø	èVy ø

æ p		ö	. Тогда
Пусть прямая l представлена тензором L вида (7), L = ç	0	÷	. Тогда
èV		ø

параметрические

функции

æ x(t) ö

координат

точек

прямой

è y(t)ø

представляются в виде вектора L0 + t × L1 .

В случае, когда прямая l задана точкой p0 = (p0x, p0y), p0

l, и вектором

нормали N = (N

, N

)

направляющий вектор прямой можно записать,

используя координаты нормали: V = (−Ny , N x ) .

Рассмотрим случай, когда прямая l задана двумя точками a

l, b

l, a

≠ b. Здесь в качестве точки p0 можно взять точку a,

качестве

направляющего вектора V прямой – вектор b - a.

Параметрическое уравнение прямой, проходящей через точки a и b,

примет вид

p(t) = a + (b − a)t, t R

(17)

4.3.3 Уравнение прямой lort, перпендикулярной заданной прямой l

Пусть заданы прямая l и точка q l . При этом в среде MathCAD они

представлены соответственно в виде (7) и (1). Будем решать следующие задачи: представить в каноническом виде (7) прямую lort, перпендикулярную заданной прямой l и проходящую через точку q l , а

также построить модели общего и параметрического уравнений прямой lort. 12

Для представления прямой lort в виде (7) следует построить тензор

æ q	ö	, где заданная точка q	lort, Vort - направляющий вектор прямой lort.
ç	÷
èVort ø

Определим координаты направляющего вектора Vort прямой lort. Пусть заданная прямая l имеет направляющий вектор с координатами V = (Vx ,Vy ) . Согласно договоренности, вектор нормали к прямой имеет

правую ориентацию к направляющему вектору этой прямой: если V = (Vx ,Vy ) , то N = (Vy ,−Vx ) . Этот же вектор N можно взять в качестве

направляющего вектора прямой lort. Таким образом, Vort = N = (Vy ,−Vx ) .

Тогда координаты	нормального вектора	прямой	lort запишутся в виде
Nort = (−Vx ,−Vy ) , или Nort = −V .
Теперь, когда определены направляющий Vort и нормальный Nort
векторы прямой	lort, а также точка	q lort, модели общего и
параметрического	уравнений прямой lort	можно	построить, используя

представления (11), (13), (15).

4.4Точка и прямая

4.4.1 Принадлежность множества точек плоскости одной прямой

Пусть заданы n точек плоскости p1 , p2 ,..., pn .

Утверждение 8. Точки p1 , p2 ,..., pn принадлежат прямой тогда и только тогда, когда ранг матрицы, столбцами которой являются координаты векторов pi − p1 , i = 2,n , равен 1.

Смотри также [1, c. 18].

4.4.2 Ориентация точки относительно прямой

Компьютерная геометрия оперирует числами, формулами и алгоритмами. Поэтому многие свойства геометрических объектов, очевидные при визуализации этих объектов, трудно определить, имея лишь представление их в среде моделирования.

Свойство прямой. Прямая l делит плоскость на две полуплоскости. Полуплоскость – совокупность точек плоскости, лежащих по одну сторону от некоторой прямой этой плоскости.

Чтобы определить, по какую сторону от прямой лежит заданная точка, удобно использовать общее уравнение прямой l. Для представления общего уравнения прямой в MathCAD можно использовать одно из выражений (10), (11), (13), (14). Для удобства сведем эти выражения в таблицу.

Пусть в среде моделирования MathCAD произвольная точка плоскости представлена вектором вида p = (x, y), в проективных

координатах - pp = (x, y,1) . Тогда левая часть общего уравнения прямой Ax + By + D = 0 может быть представлена одним видов 1-4, см. таблицу.

Данные для представления

Модель для представления выражения

общего уравнения прямой l

Ax + By + D

Вектор F параметров

FT pp

общего уравнения прямой

Вектор нормали N и точка

(p - p )

p l

Направляющий вектор прямой V

p - p0

и точка p0 l

Точки a Îl , bÎl , a ¹ b

p − a

b − a

Левую часть уравнения

Ax + By + D = 0 , независимо от модели, его

задающей, обозначим f ( p),

где

p –

произвольная точка

плоскости с

координатами x, y.

Выражение f ( p) = 0 удобно

тем, что оно позволяет

эффективно

определять

∙принадлежность произвольной точки p прямой линии l;

∙взаимное расположение двух точек a и b относительно прямой f ( p) = 0 .

Утверждение 9.

Точка q принадлежит прямой l тогда и только тогда, когда f (q) = 0.

С учетом соглашения о левой ориентации направляющего вектора V относительно вектора нормали N, получим тест, определяющий положение точки q относительно направления движения по прямой l вдоль вектора V: при f(q) > 0 точка q лежит справа от прямой l,

при f(q) < 0 точка q лежит слева от прямой l.

Утверждение 10.

Точки плоскости a и b расположены по одну сторону от прямой l тогда и только тогда, когда f (a) f (b) > 0 . Точки плоскости a и b

расположены по разные стороны от прямой l тогда и только тогда, когда f (a) f (b) < 0 .

4.4.3 Расстояние от точки до прямой

Пусть заданы прямая l и точка q l . При этом в среде MathCAD они

представлены соответственно в виде (7) и (1). Представим в MathCAD выражение, вычисляющее расстояние от точки q l до прямой l.

Из курса аналитической геометрии известно, что расстояние от точки q l до прямой l равно результату подстановки координат данной точки в

левую часть уравнения прямой l в нормальном виде.

Уравнение вида Ax + By + D = 0 называют уравнением прямой в

нормальном виде, если N = 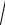(A, B) o (A, B) =1. Если N ¹ 1, то общее уравнение (9) прямой можно привести к нормальному виду, умножив обе

его части на множитель N .

Утверждение 11. Расстояние от точки q до прямой l в среде MathCAD может быть представлено в виде

d =	FT	× qq	,	(18)
		N


æ A ö				æ qx	ö
где F = çç B ÷÷ - вектор параметров общего уравнения прямой l,				ç	÷	-
				qq = ç qy ÷		-
ç ÷				ç	÷
è D ø				è1	ø

проективный вектор точки q.

Знак величины d указывает взаимное расположение точки q и вектора нормали относительно прямой l.

Смотри также [1, c. 20].

4.4.4 Зеркальное отражение точки относительно прямой

Пусть заданы прямая l и точка q l . Рассмотрим задачу зеркального отражения точки относительно прямой l.

Результатом отображения точки q является точка, назовем ее qIm . Точка qIm лежит на прямой, перпендикулярной заданной прямой l на

расстоянии 2|d| от точки q, где d - расстояние от точки до прямой. Смотри также [1, c. 20].

4.5Расположение прямых

4.5.1Взаимное расположение двух прямых

Смотри [1, c. 19].

4.5.2Расстояние между двумя параллельными прямыми

Смотри [1, c. 19].

4.5.3Точка пересечения двух прямых

Пусть каждая из прямых l1 и l2 ,				пересекающихся в точке q = l1 Ç l2 ,
задана точкой p0i		li,	p0i = (x0i y0i )T	и вектором нормали Ni = ( Ai	Bi )T
к прямой l	, i = 1, 2.		Вычислить координаты точки пересечения		этих
i

прямых.

Согласно (11), если прямая задана точкой p0

l и вектором нормали

N, то произвольная точка p

l удовлетворяет условию

NT ( p - p

) = 0 .

Так как q = l

Ç l

ïN1

(q p01 ) = 0

, то í

ïN

T (q - p ) = 0

или в координатном виде

æ x

- x

(Ai

)

= 0 , i = 1, 2

ç y

- y

откуда

A B

öæ xq ö

A x + B y

÷ =

1 01

A B

÷ç y

A x + B y

øè

q ø

2 02

Тогда искомый вектор-столбец координат точки q пересечения двух

прямых может быть вычислен по формуле

æ xq

A B

ö−1 æ

A x + B y

(19)

÷=

1 01

ç y

A B

A x + B y

q ø

2 02

	Смотри также [1, c. 24].
	Пусть каждая из прямых l1 и l2 , пересекающихся в точке q = l1 Ç l2 ,
задана точкой p0i		li и направляющим вектором Vi = (Vxi Vyi )T						к прямой
l	, i = 1, 2. Вычислим значения параметров точки пересечения этих прямых.
i	Пусть точке	q = l1 Ç l2 соответствует вектор параметров						(t* ,τ * ) .
	Пусть точке	q = l1 Ç l2 соответствует вектор параметров						(t* ,τ * ) .
		ì			*
		ì		+ V1t ,
		ïq = p01		+ V1t ,			,
Тогда имеет место í				+ V τ		*	,
		ïq = p	02	+ V τ		*
		î	02	2

откуда,

вычитая

из

первого

уравнения

второе,

получим

V t* - V τ * = p

- p

Запишем последнее выражение в координатном виде

æV

æ x - x

÷t* -

÷τ *

= ç

÷ ,

èVy1 ø

èVy 2 ø

è y02 - y01 ø

- Vx2τ

= x02 - x01

ïVx1t

что соответствует системе уравнений íV

- V

τ *

= y

- y

которую можно представить в матричной форме

æV

- V

öæt* ö

æ x - x

÷ç

= ç

÷ .

* ÷

è y02 - y01

èVy1

- Vy2 øèτ

Искомый вектор параметров точки пересечения прямых может быть вычислен по формуле

æt* ö		æVx1
ç	÷	= ç
ç	* ÷	ç
èτ	ø	èVy1

Смотри также [1, c. 25].

4.5.4 Пучок прямых

Смотри [1, c. 25-27].

- V	x2	ö−1	æ x	- x	ö	(20)
	x2	÷	ç 02	01	÷ .	(20)
- Vy2 ø			è y02 - y01 ø

5. Задачи и упражнения

5.1Точка, вектор, прямая

1.Построить функцию PointPol2Dek(PhiRho), которая по заданным координатам точки p в полярной системе координат определяет ее положение в декартовой системе координат. Системы координат соотносятся следующим образом: полюс совпадает с началом координат

вдекартовой системе, а полярная ось – с положительным направлением оси ОХ. Входной аргумент PhiRho – вектор вида [φ, ρ]Т, где φ –

полярный угол, ρ – полярный радиус точки p. Функция возвращает вектор вида [px, py]Т, где px и py – соответственно координаты x и y точки p в прямоугольной декартовой системе координат.

2.Построить функцию VectorOrt(Vec), возвращающую орт заданного вектора Vec.

3.Построить функцию ShowVector(Vec, apPoint), возвращающую модель вектора Vec для его отображения. Входные параметры: Vec – каноническое представление вектора в MathCAD, apPoint – точка приложения вектора.

4.Построить функцию, вычисляющую направление биссектрисы угла между двумя заданными векторами.

5.Создать функцию, возвращающую проекцию вектора V на вектор W.

6.Создать функцию Line(a, b), которая представляет в MathCAD прямую l на плоскости. Входные аргументы – точки a l, b l, a ≠ b. Выход: структура данных тензор – вектор, первый элемент которого – точка p0 l, второй – направляющий вектор прямой V вида [Vx, Vy]Т. Каждая точка представлена в каноническом виде.

7.Создать функцию Line(p0, N), которая представляет в MathCAD прямую l на плоскости. Входные аргументы – точка p0 l, N – нормальный вектор

прямой вида [Nx, Ny]Т. Выход: структура данных тензор – вектор,

первый элемент которого – точка p0 l, второй – направляющий вектор прямой l. Точка p0 представлена в каноническом виде.

8. Построить функцию ShowLineX(line, xLeft, xRight, ), которая возвращает
ɛ	ɛ			указанных по оси ОХ пределах
данные для отображения прямой line в					ɛ
[xLeft - , xRight + ].		Входной	параметр		line	–	каноническое
представление прямой в MathCAD.
9. Построить функцию ShowLineY(line, yLow, yTop, ), которая возвращает
ɛ	ɛ			указанных по оси ОY пределах
данные для отображения прямой line в					ɛ
[yLow - , yTop +	].	Входной	параметр		line	–	каноническое
представление прямой в MathCAD.


10.	Прямая line на плоскости задана вектором параметров общего
уравнения прямой F = [A B D]. Написать функцию, тестирующую
принадлежность заданной точки p прямой line.
11.	Прямая line на плоскости задана точкой		p0 l	и направляющим
вектором V. Написать функцию,		тестирующую		принадлежность

заданной точки p прямой line.
12.	Прямая line на плоскости задана точкой p0		l и вектором N нормали к

прямой. Написать функцию, тестирующую принадлежность заданной
точки p прямой line.
13. Прямая line на плоскости задана двумя точками a l, b l, a ≠ b.

Написать функцию, тестирующую принадлежность заданной точки p прямой line.

14. Прямая line на плоскости задана вектором параметров общего уравнения прямой F = [A B D]. Написать функцию, тестирующую взаимное расположение двух заданных точек p и q относительно прямой

15.Прямая l на плоскости задана точкой p0 l и направляющим

вектором V. Написать функцию, тестирующую взаимное расположение двух заданных точек p и q относительно прямой l.

16.Прямая l на плоскости задана точкой p0 l и вектором N нормали к прямой. Написать функцию, тестирующую взаимное расположение двух

17.Прямая l на плоскости задана двумя точками a l, b l, a ≠ b.

Написать функцию, тестирующую взаимное расположение двух заданных точек p и q относительно прямой l.

18. Для прямой line на плоскости, заданной вектором параметров общего уравнения прямой F = [A B D], написать функцию, возвращающую

направляющий вектор этой прямой. Вектор имеет левую ориентацию относительно нормального вектора прямой.

19.Написать функцию, возвращающую вектор параметров F = [A B D] общего уравнения прямой, если прямая l задана точкой p0 l и направляющим вектором V.

20.Написать функцию, возвращающую вектор параметров F = [A B D] общего уравнения прямой, если прямая l задана точкой p0 l и вектором

N нормали к прямой.

21.Создать функцию, тестирующую, лежат ли заданные n точек плоскости на одной прямой.

22.Создать функцию, тестирующую взаимное направление двух векторов плоскости. Варианты ответов:

-1 против направлены 0 не параллельны и не перпендикулярны 1 со направлены 2 перпендикулярны

23.Написать функцию, возвращающую представление в MathCAD прямой lOrt, которая перпендикулярна заданной прямой l и проходит через заданную точку q. Прямая l задана вектором параметров общего уравнения прямой F = [A B D].

24.Написать функцию, возвращающую представление в MathCAD прямой lOrt, которая перпендикулярна заданной прямой l и проходит через заданную точку q. Прямая l задана точкой p0 l и направляющим вектором V.

25.Написать функцию, возвращающую представление в MathCAD прямой lOrt, которая перпендикулярна заданной прямой l и проходит через заданную точку q. Прямая l задана точкой p0 l и вектором N нормали к прямой.

26.Написать функцию, вычисляющую расстояние от заданной точки q до прямой l. Прямая l задана вектором параметров общего уравнения прямой F = [A B D].

27.Написать функцию, вычисляющую расстояние от заданной точки q до прямой l. Прямая l задана точкой p0 l и направляющим вектором V.

28.Написать от заданной точки q до прямой l. Прямая l задана точкой p0 l и вектором N нормали кфункцию, вычисляющую расстояние

прямой.

29. На плоскости заданы прямая line и случайным образом распределенные n точек. Создать функцию, разделяющую множество заданных n точек на три подмножества: точки, лежащие на прямой, и 19

точки, лежащие по одну либо другую сторону прямой. Нарисовать заданные объекты, изобразив точки, лежащие по одну сторону от прямой line, синим цветом, по другую сторону от прямой – красным.

30. Прямые line1 и line2 заданы векторами параметров общего уравнения. Определить их взаимное расположение. Варианты ответов: -1 не пересекаются

0совпадают

1пересекаются не ортогонально

2пересекаются ортогонально

Изобразить прямые и точку пересечения, если она существует.

31. Каждая из прямых l1 и l2 задана точкой p0i li и направляющим вектором Vi, i = 1,2. Определить взаимное расположение прямых. Варианты ответов:

-1 не пересекаются

0совпадают

1пересекаются не ортогонально

2пересекаются ортогонально

Изобразить прямые и точку пересечения, если она существует.

32. Каждая из прямых l1 и l2 задана точкой p0i li и вектором нормали к прямой Ni, i = 1,2. Определить взаимное расположение прямых. Варианты ответов:

-1 не пересекаются

0совпадают

1пересекаются не ортогонально

2пересекаются ортогонально

Изобразить прямые и точку пересечения, если она существует.

33.Две параллельные прямые line1 и line2 заданы векторами параметров общего уравнения. Написать функцию, вычисляющую расстояние между ними.

34.Написать функцию, вычисляющую расстояние между двумя параллельными прямыми l1 и l2, каждая из которых задана точкой p0i li

инаправляющим вектором Vi, i = 1,2.

35.Написать функцию, вычисляющую расстояние между двумя параллельными прямыми l1 и l2, каждая из которых задана точкой p0i li и

вектором нормали к прямой Ni, i = 1,2.

36. Написать функцию, вычисляющую точку пересечения двух прямых l1 и l2, каждая из которых задана вектором параметров общего уравнения прямой.

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.11.2018107.52 Кб32011г.План сем. зан.ОЭТ.doc
#
21.08.20193.92 Mб272012-ОТВЕТЫ-ГЭК.docx
#
03.05.20192.6 Mб42012_ИГФ-ФК_Лабораторная_работа_№1.doc
#
03.05.20191.73 Mб62012_ИГФ_ФК_Приложение_к_Лабораторной_работе_№1...doc
#
15.11.2019113.15 Кб22012г.План сем. зан.ОЭТ.doc
#
01.03.2016229.96 Кб72014 КМ1 УСР3(пед).pdf
#
29.02.2016134.21 Кб132014-2015_ekz_bil_upravl_riskami_1 (2).docx
#
15.04.201960.42 Кб120_Politika_rossyskogo_tsarizma_v_Belarusi.doc
#
02.08.201931.42 Кб121,22,23,24,25,26,28,29,30.docx
#
29.02.201645.53 Кб2121-24.docx
#
21.04.201931.76 Кб221-24.docx