
Основы автоматизации Ямный,Яновский
.pdf
Лекция 5 КОМБИНАЦИОННЫЕ СХЕМЫ
Комбинационными называются такие цифровые схемы, выходные сигналы которых в каждый момент времени определяются совокупностью входных сигналов и не зависят от их предыдущих состояний. В комбинационных схемах (КС) нет памяти, которая могла бы содержать ранее полученную информацию. Их работа полностью определяется таблицами истинности и описывается с помощью структурных формул.
5.1.Анализ и синтез комбинационных схем
Втеории комбинационных схем рассматриваются две основные задачи: задача анализа и задача синтеза.
Анализ КС. Задача анализа КС может быть сформулирована как задача нахождения структурной формулы, описывающей работу заданной схемы.
При решении этой задачи устанав-
ливается однозначное соответствие между логическими элементами КС и ее математическим описанием.
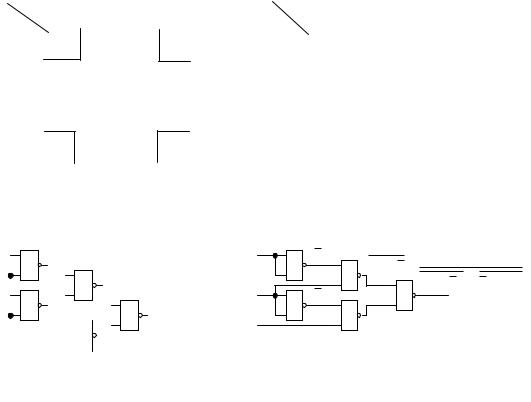
С решением задачи анализа ознакомимся на примере КС, приведенной на рис. 5.1. Непосредственно из схемы имеем
x1 A1
A3 y1
x2 A2
y2
x3 A4
Рис.5.1. Комбинационная схема
A1 = x1 , A2 = x2 , A3 = x1 x2 ,
A4 = x2 + x3 , y1 = A3 + A4 = x1 x2 +(x2 + x3 ),
y2 = A3 A4 = x1 x2 (x2 + x3 ) .
Как видно из приведенного примера, анализ КС не вызывает принципиальных затруднений.
Синтез КС. Задача синтеза может быть сформулирована как задача построения цифрового устройства, реализующего заданную булеву функцию в заданном базисе логических элементов.
Синтез КС производится в несколько этапов. На первом этапе составляют аналитическое описание (систему структурных формул в СДНФ или в СКНФ) заданных, как правило, таблично булевых функций. На втором этапе минимизируют полученные структурные формулы и осуществляют переход в заданный базис. При этом при переходе в базис
51

И-НЕ обычно используют структурные формулы в СДНФ, а при переходе в базис ИЛИ-НЕ – структурные формулы в СКНФ.
На заключительном этапе синтеза осуществляют переход от минимизированных структурных формул к структурной схеме КС.
В качестве примера рассмотрим синтез КС, реализующей функцию у', заданную таблично (табл. 5.1). На первом этапе синтеза получим структурную формулу функции у' в СДНФ
y'1= x3 x2 x1x0 + x3 x2 x1 x0 + x3 x2 x1x0 + x3 x2 x1x0 + x3 x2 x1x0 + |
|
+ x3 x2 x1x0 + x3 x2 x1x0 + x3 x2 x1x0 |
(5.1) |
и структурную формулу этой же функции в СКНФ
y'2 = (x3 + x2 + x1 + x0 )· (x3 + x2 + x1 + x0 )· (x3 + x2 + x1 + x0 )х
х(x3 + x2 + x1 + x0 )· (x3 + x2 + x1 + x0 )· (x3 + x2 + x1 + x0 )х |
|
х(x3 + x2 + x1 + x0 )·(x3 + x2 + x1 + x0 ). |
(5.2) |
Таблица 5.1
Номер |
x3 |
x2 |
x1 |
x0 |
y' |
y" |
набора |
||||||
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
Ф |
2 |
0 |
0 |
1 |
0 |
1 |
1 |
3 |
0 |
0 |
1 |
1 |
0 |
1 |
4 |
0 |
1 |
0 |
0 |
0 |
1 |
5 |
0 |
1 |
0 |
1 |
0 |
1 |
6 |
0 |
1 |
1 |
0 |
1 |
0 |
7 |
0 |
1 |
1 |
1 |
1 |
0 |
8 |
1 |
0 |
0 |
0 |
1 |
Ф |
9 |
1 |
0 |
0 |
1 |
0 |
0 |
10 |
1 |
0 |
1 |
0 |
1 |
0 |
11 |
1 |
0 |
1 |
1 |
0 |
0 |
12 |
1 |
1 |
0 |
0 |
0 |
0 |
13 |
1 |
1 |
0 |
1 |
0 |
0 |
14 |
1 |
1 |
1 |
0 |
1 |
Ф |
15 |
1 |
1 |
1 |
1 |
1 |
1 |
На втором этапе булевы функции (5.1) и (5.2) минимизируются, например, с помощью представленных на рис. 5.2 карт Карно. Полученная при этом структурная формула в сокращенной дизъюнктивной нормальной форме используется для представления функции у' в базисе И-НЕ
у'1 = x2 x1 + x2 x0 = x2 x1 x2 x0 . (5.3)
Полученная в результате минимизации булевой функции структурная формула в сокращенной конъюнктивной нормальной форме используется для представления функции у' в базисе ИЛИ-НЕ
у'2 = |
(x2 + x1 )(x2 + x0 ) |
= |
x2 + x1 |
+ |
x2 + x0 |
. |
(5.4) |
Структурные схемы синтезированного цифрового устройства в базисе И-НЕ и в базисе ИЛИ-НЕ приведены на рис. 5.3, а и рис. 5.3, б соответственно.
52
x1x0 |
00 |
01 |
11 |
10 |
|
|
x1x0 |
00 |
|
|
01 |
11 |
|
|
10 |
|
|
|||
x3x2 |
|
|
x3x2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
00 |
1 |
0 |
0 |
1 |
|
|
00 |
|
1 |
|
|
0 |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
|
01 |
|
0 |
0 |
|
1 |
|
|
1 |
|
|
|||||||
11 |
0 |
0 |
1 |
1 |
|
|
11 |
|
0 |
0 |
|
1 |
|
|
1 |
|
|
|||
10 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
а |
|
1 |
|
0 |
|
0 |
|
|
1 |
|
б |
||||||||
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|||
|
y1′ = x2 x1 + x2 x0 |
|
= (x2 + x1)(x2 + x0 ) |
|
||||||||||||||||
|
|
y2 |
|
|||||||||||||||||
Рис. 5.2. Минимизация функции у' в СДНФ (а) и в СКНФ (б)
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
& |
x |
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x2 |
|
& |
|
|
|
|
|
|
|
х |
х |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
х |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
х |
|
х |
|
|
|
|
||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
& |
|
|
|
2 |
0 |
2 |
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
а) |
|
|
а |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2 х |
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x 0 |
1 |
x0 |
|
|
|
|
|
|
1 |
х2 |
+ х0 |
|
|
||
x2 |
|
х2 |
+ х0 + х2 + х1 |
||||
|
|
||||||
|
x2 |
|
|
1 |
|||
x1 |
1 |
1 |
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 + х |
1 б) |
б |
х |
Рис. 5.3. Комбинационная схема в базисе И-НЕ (а) и в базисе ИЛИ-НЕ (б)
5.2. Сумматоры и вычитатели
Сложение является основной арифметической операцией, выполняемой в цифровых устройствах. Другие арифметические операции – вычитание, умножение, деление – сводятся к сложению. КС, выполняющие операцию «сложение», называются сумматорами. Применяются одноразрядные и многоразрядные сумматоры.
Одноразрядные двоичные сумма-
торы. Одноразрядные двоичные сумматоры могут быть полными и неполными. Неполный двоичный сумматор (полусумматор) предназначен для сложения двух одноразрядных двоичных чисел. Составленные в соответствии с таблицей истинности полусумматора (табл. 5.2) структурные формулы булевых функций SM и CR имеют вид:
Таблица 5.2
Таблица истинности двоичного полусумматора
Слагаемые |
Сумма |
Перенос |
|
|
|
SM |
CR |
a |
b |
||
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
SM = |
a |
b + a |
b |
= a b, CR = a b. |
(5.5) |
53
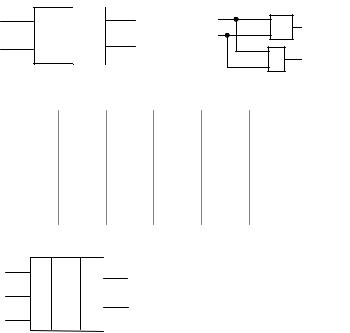
Условное обозначение полусумматора и его структурная схема приведены на рис. 5.4. Временные диаграммы сигналов полусумматора, реализованного на ИС КР1533, приведены на рис. 5.5. Из них видно, что выходные сигналы полусумматора формируются с задержкой относительно его входных сигналов.
a b
HS ∑
CR
|
b |
|
SM |
SM |
a |
=1 |
|
a |
SM |
||
CR |
b |
|
CR |
|
& |
Рис. 5.4. Условное обозначение (а) и структурная схема (б) полусумматора
|
|
а |
|
|
|
|
|
|
|
|
б |
|||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.5. Временные диаграммы |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
SM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сигналов полусумматора |
|
CR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 нс |
100 нс 150 нс 200 нс 250нс |
||||||||||||
ai |
А SM |
∑ |
|
|
SMi |
|
Полный (одноразрядный) двоичный сумма- |
|||||||
|
|
|
||||||||||||
bi |
|
|
||||||||||||
B |
|
|
|
CRi |
|
тор формирует сигнал суммы SMi и сигнал пере- |
||||||||
CRi–1 |
СR |
CR |
|
|
носа CRi в старший разряд в соответствии с сиг- |
|||||||||
|
|
|
|
|
|
|
|
|
налами ai и bi двух i-х разрядов слагаемых и сиг- |
|||||
Рис. 5.6. Условное |
|
|||||||||||||
|
нала CRi–1 переноса из предыдущего (i–1)-го раз- |
|||||||||||||
обозначение полного |
|
|||||||||||||
одноразрядного |
|
|
ряда. Условное обозначение полного двоичного |
|||||||||||
|
|
сумматора приведено на рис. 5.6. |
||||||||||||
|
сумматора |
|
|
|||||||||||
Составленные в соответствии с табл. 5.3 структурные формулы булевых функций SMi и CRi полного двоичного сумматора в СДНФ имеют вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SMi = ai bi CRi–1 + ai |
bi |
|
CR i–1 + |
a |
i |
b |
i |
CRi–1 + |
a |
ibi CR i–1, |
|
|||||||
CRi = ai bi CRi–1 + ai bi |
|
i–1 + ai |
|
CRi–1 + |
|
ibi CRi–1. |
(5.6) |
|||||||||||
CR |
||||||||||||||||||
bi |
a |
|||||||||||||||||
Можно различным образом преобразовать выражения (5.6) и получить много различных вариантов реализации функций суммы и переноса. Например, выражения
SMi = ai bi CRi–1,
CRi = ai·bi + CRi–1 (ai bi) |
(5.7) |
показывают возможность реализации полного одноразрядного сумматора на двух полусумматорах и логическом элементе ИЛИ (рис. 5.7). Временные диаграммы сигналов такого сумматора, реализованного на ИС КР1533, приведены на рис. 5.8.
54
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.3 |
CRi–1 |
|
|
|
|
|
|
|
|
SMi |
||||||||||||||
Таблица истинности полного двоичного |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
HS |
Σ |
|||||||||||||||||||||||||||||||
|
|
|
|
|
сумматора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Слагаемые |
|
Перенос |
|
|
Сумма |
|
|
|
Перенос |
|
|
|
|
|
|
|
|
|
CR |
|
|
|
|
|
|
|
|
|
||||||||
ai |
|
bi |
|
|
CRi–1 |
|
|
|
SMi |
|
|
|
CRi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
0 |
|
0 |
|
0 |
|
0 |
|
|
|
ai |
|
|
|
|
HS |
Σ |
|
|
|
|
|
|
|
CRi |
|||||||||||
0 |
0 |
|
1 |
|
1 |
|
0 |
|
|
|
bi |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||
0 |
1 |
|
0 |
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
CR |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
1 |
|
1 |
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
0 |
|
0 |
|
1 |
|
0 |
|
|
|
Рис. 5.7. Структурная |
|||||||||||||||||||||||||
1 |
0 |
|
1 |
|
0 |
|
1 |
|
|
|
|
|
|
схема полного |
||||||||||||||||||||||
1 |
1 |
|
0 |
|
0 |
|
1 |
|
|
|
|
одноразрядного |
||||||||||||||||||||||||
1 |
1 |
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
сумматора |
|||||||||||||||||||||
CRi–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ai |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
SMi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
CRi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 нс |
|
100 нс |
150 нс 200 нс 250 нс |
300 нc 350 нс |
400 нс |
|||||||||||||||||||||||||||||
Рис. 5.8. Временные диаграммы сигналов полного сумматора
Параллельные многоразрядные сумматоры. Параллельные многораз-
рядные сумматоры состоят из группы одноразрядных сумматоров, число которых определяется разрядностью суммируемых чисел. Простейшими из параллельных сумматоров являются сумматоры с последовательным переносом (рис. 5.9). Сложение многоразрядных чисел в подобных сумматорах предусматривает одновременную подачу всех разрядов слагаемых, а процесс суммирования осуществляется последовательно, так как сигнал суммы в каждом разряде сумматора может быть сформирован лишь при наличии сигнала переноса из предыдущего разряда.
Реализация параллельных сумматоров с последовательным перено-
|
|
|
|
|
|
|
SM0 |
|
|
SM1 |
|
|
|
SM2 |
|
|
|
|
|
|
SM3 CR3 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
SM |
SM |
|
|
|
|
|
A |
SM |
|
SM |
|
|
|
|
|
A |
SM |
SM |
|
|
|
|
|
A |
SM |
|
SM |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
B |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
CR |
|
CR |
|
|
|
|
|
CR |
|
|
CR |
|
|
|
|
|
CR |
|
CR |
|
|
|
|
|
CR |
|
|
CR |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 |
|
b0 |
|
«1» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а1 b1 |
|
|
|
|
|
|
а2 |
b2 |
|
|
|
|
а3 b3 |
|
|
|
|
|
|
|||||||||||||||
Рис. 5.9. Параллельный сумматор с последовательным переносом
55
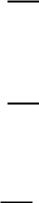
сом не вызывает затруднений, однако быстродействие их невелико. Более высокое быстродействие обеспечивают параллельные сумматоры со сквозным переносом.
Дальнейшее увеличение быстродействия имеет место в сумматорах с ускоренным переносом, в которых операция сложения выполняется как поразрядная операция и на распространение сигнала переноса дополнительное время не требуется. В таких сумматорах сигнал переноса в каждом разряде формируется одновременно с поступлением сигнала переноса в младший разряд.
Вычитатели двоичных чисел. Операцию вычитания двоичного чис-
ла B = bn–1 bn–2 ... b1 b0 из числа A = an–1 an–2 ... a1 a0 можно выполнить с помощью многоразрядного вычитающего устройства, построенного на
одноразрядных полных вычитателях.
Однако более предпочтительным является устройство, в котором арифметические операции сложения и вычитания выполнены на полных сумматорах. Принципиальная возможность построения такого устройства основана на возможности замены операции арифметического вычитания операцией алгебраического сложения чисел, представленных в дополнительном или в обратном коде.
В общем случае в зависимости от используемого для представления двоичных чисел кода различают многоразрядные сумматоры прямого кода, дополнительного кода и обратного кода (рис. 5.10).
Двоичный сумматор прямого кода можно использовать для сложе-
|
|
|
|
|
|
|
|
|
|
|
|
|
SM0 |
|
|
|
|
|
|
|
|
|
|
|
SM1 |
|
|
|
|
|
|
|
|
|
|
|
SMn–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
SMЗН |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
а0 |
|
|
|
|
|
|
|
|
|
|
а1 |
|
|
|
|
|
|
|
|
|
|
|
аn–1 |
|
|
|
|
|
|
|
|
|
|
|
|
азн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
A |
|
SM |
SM |
|
|
A |
|
SM |
SM |
|
|
|
A |
|
SM |
SM |
|
|
|
|
A |
|
SM |
SM |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
b0 |
|
B |
|
|
|
|
|
b1 |
|
B |
|
|
|
|
|
|
bn–1 |
|
|
B |
|
|
|
|
|
|
bзн |
|
|
|
B |
|
|
|
|
|
|
|
CRЗН |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
«0» |
|
|
CR |
|
|
CR |
|
|
|
|
|
CR |
|
|
CR |
|
|
|
|
|
|
|
CR |
|
|
CR |
|
«0» |
|
|
|
|
CR |
|
|
CR |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
а |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
SM0 |
|
|
|
|
|
|
|
|
|
|
|
SM1 |
|
|
|
|
|
|
|
|
|
|
|
SMn–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
SMЗН |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
а0 |
|
|
|
|
|
|
|
|
|
|
|
а1 |
|
|
|
|
|
|
|
|
|
|
|
|
аn–1 |
|
|
|
|
|
|
|
|
|
|
|
|
азн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
A |
|
SM |
SM |
|
|
A |
|
SM |
SM |
|
|
|
A |
|
SM |
SM |
|
|
|
|
A |
|
SM |
SM |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
b0 |
|
|
B |
|
|
|
|
|
b1 |
|
|
B |
|
|
|
|
|
|
bn–1 |
|
|
B |
|
|
|
|
|
|
bзн |
|
|
|
B |
|
|
|
|
|
|
|
CRЗН |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
«0» |
|
|
CR |
|
|
CR |
|
|
|
|
|
CR |
|
|
CR |
|
|
|
|
|
|
|
CR |
|
|
CR |
|
|
|
|
|
|
|
|
CR |
|
|
CR |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CRn-1 |
|
|
|
|
|
|
|
б |
б |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
SM0 |
|
|
|
|
|
|
|
|
|
|
|
SM1 |
|
|
|
|
|
|
|
|
|
SMn–1 |
|
|
|
|
|
|
|
|
|
|
|
|
SMЗН |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
а0 |
|
|
|
|
|
|
|
|
|
а1 |
|
|
|
|
|
|
|
|
аn–1 |
|
|
|
|
|
|
|
|
|
|
азн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
A |
|
SM |
SM |
|
|
A |
|
SM |
SM |
|
A |
|
SM |
SM |
|
|
|
|
A |
|
SM |
SM |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
b0 |
|
B |
|
|
|
|
|
|
b1 |
|
B |
|
|
|
|
|
bn–1 |
|
B |
|
|
|
|
|
|
|
bзн |
|
|
B |
|
|
|
|
|
CRЗН |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
CR |
|
|
|
CR |
|
|
|
|
|
CR |
|
|
|
CR |
|
|
|
|
|
|
|
CR |
|
|
|
CR |
|
|
|
|
|
|
|
CR |
|
|
|
CR |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
в |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 5.10. Структурная схема двоичных сумматоров прямого (а), дополнительного (б) и обратного (в) кодов
56
ния чисел, имеющих одинаковые знаки. Характерной особенностью такого сумматора является отсутствие поразрядного переноса между старшим значащим и знаковым разрядами (рис. 5.10, а).
Двоичный сумматор с цепью поразрядного переноса из старшего значащего разряда в знаковый (рис. 5.10, б) является двоичным сумматором дополнительного кода. Он выполняет алгебраическое сложение двоичных чисел, представленных в дополнительном коде.
Алгебраическое сложение двоичных чисел, представленных в обратном коде, осуществляет двоичный сумматор обратного кода. Характерной особенностью такого сумматора является наличие не только цепи поразрядного переноса из старшего значащего разряда в знаковый разряд, но и цепи циклического переноса из знакового разряда в младший значащий разряд (рис. 5.10, в).
Сложение и вычитание десятичных чисел, представленных в коде
8-4-2-1. Сложение десятичных чисел, представленных в двоичнодесятичном коде, выполняется, как правило, в рамках каждого десятичного разряда, т. е. в рамках каждой тетрады. Сумматор для одной тетрады представляет собой устройство, которое имеет 8 входов для ввода двоичных символов ai', bi', ci', di' и ai'', bi'', ci'', di'', образующих десятичные разряды слагаемых, и один вход для сигнала десятичного переноса из младшей тетрады. Такой сумматор имеет 4 выхода суммы SM0, SM1, SM2, SM3 и выход десятичного переноса в старшую тетраду.
При реализации подобных суммирующих устройств на основе двоичных сумматоров возникают определенные трудности, обусловленные необходимостью вырабатывать десятичный перенос и производить коррекцию результата, из-за того, что тетрада реализует 16 различных комбинаций, а в любом двоично-десятичном коде используется только десять.
Большинство микропроцессоров и микроконтроллеров содержат программно-управляемые средства выполнения десятичной коррекции. Они осуществляют коррекцию результата сложения двоичным сумматором десятичных чисел, представленных в двоично-десятичном коде 8-4-2-1, когда при сложении получаются недопустимые комбинации (1010,…,1111) или формируется перенос из младшей тетрады в следующую старшую. Коррекция полученного при сложении результата осуществляется путем прибавления к нему числа 610 = 01102, причем возникающие в процессе коррекции переносы учитываются.
57
5.3.Схемы сравнения двоичных чисел
Вцифровых устройствах наибольшее распространение получили два способа сравнения двоичных чисел А и В, устанавливающих факт их равенства.
Первый способ заключается в вычитании одного числа из другого и определении по полученной разности равенства или неравенства сравниваемых чисел. Этот способ нашел широкое применение в микропроцессорах и микроконтроллерах.
Операция сравнения может выполняться также с помощью комбинационной схемы, формирующей соответствующий сигнал только в случае совпадения цифр во всех разрядах сравниваемых чисел.
Для установления равенства одноразрядных двоичных чисел можно воспользоваться функцией «эквивалентность»
Ri = aibi |
+ |
a |
|
|
b |
i = |
ai |
bi |
|
ai |
|
|
(5.8) |
|||||||
i |
bi |
|||||||||||||||||||
или функцией «отрицание неравнозначности» |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ri = |
|
|
|
|
= ai |
|
|
+ |
|
|
|
. |
(5.9) |
|||||||
ai |
bi |
aibi |
||||||||||||||||||
bi |
||||||||||||||||||||
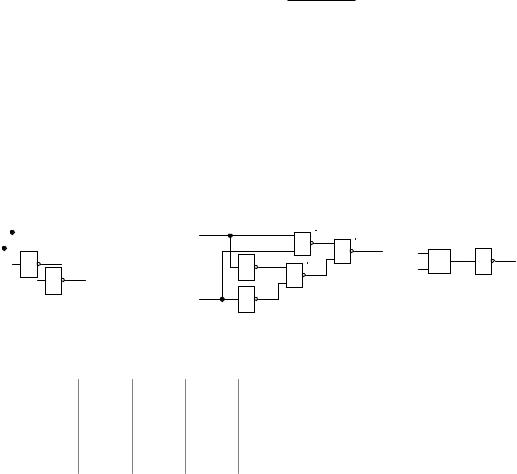
На рис. 5.11 приведены различные варианты реализации схем равенства одноразрядных двоичных чисел и изображено их условное обозначение. Временные диаграммы сигналов схемы равенства кодов (рис. 5.11, в), реализованной на ИС КР1533, приведены на рис. 5.12.
ai |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ai |
|
|
|
|
Ri ai |
|
||||
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
Ri |
|
|
& |
& |
Ri |
||||||||
bi |
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
=1 |
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
& |
|
|
bi |
|
||||
|
|
|
|
|
|
a |
|
|
|
|
bi |
1 |
б |
|
в |
|||||||||||||
|
аi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Ri |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
bi |
|
|
|
|
=1 |
|
|
|
|
г |
|
Рис. 5.11. Схемы равенства одноразрядных двоичных |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
чисел (а, б, в) и их условное обозначение (г) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
ai |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.12. Временные диаграммы |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
bi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сигналов схемы равенства одно- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разрядных двоичных чисел |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Ri |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
25 нс |
50 нс |
|
75 нс |
|
|
|
|
|
|
|
|
|||||||||
Для установления равенства n-разрядных двоичных чисел А и В необходимо реализовать функцию Ri для каждого их разряда, то есть
58
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
n−1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1(A, B) = ∏Ri |
= ∏(ai |
bi ). |
(5.10) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=0 |
|
i=0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
R0 |
|
|
|
|
|
|
|
|
|
Схема установления равенства двух- |
|||||||||||||
a0 |
|
|
|
1 |
|
|
|
|
A=B |
разрядных двоичных чисел, реализован- |
||||||||||||||||||||||
=1 |
|
|
|
|
||||||||||||||||||||||||||||
b0 |
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
ная на ИС КР1533, приведена на рис. 5.13, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
a1 |
|
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
|
а временные диаграммы ее сигналов – на |
||||||||||||||||
|
|
=1 |
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис. 5.14. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Рис. 5.13. Схема равенства двух- |
|
|
Кроме рассмотренных схем приме- |
|||||||||||||||||||||||||||||
разрядных двоичных чисел |
няются |
|
также |
|
комбинационные |
схемы, |
||||||||||||||||||||||||||
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
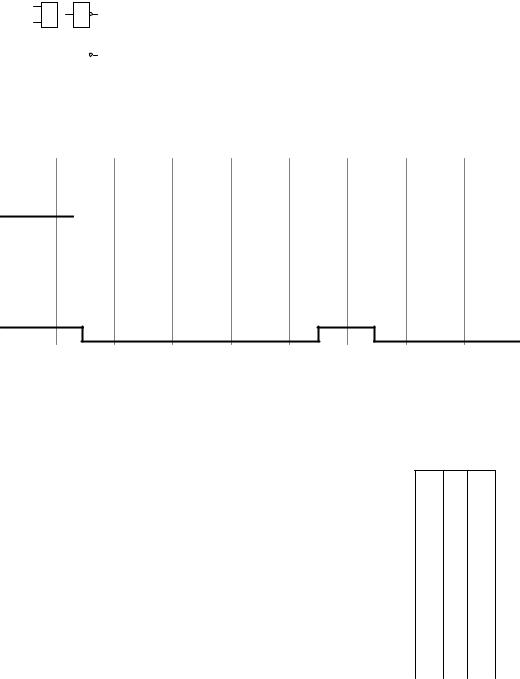
A=B
25 нс |
50 нс |
75 нс |
100 нс |
125 нс |
150 нс |
175 нс |
200 нс |
Рис. 5.14. Временные диаграммы сигналов схемы равенства двухразрядных двоичных чисел
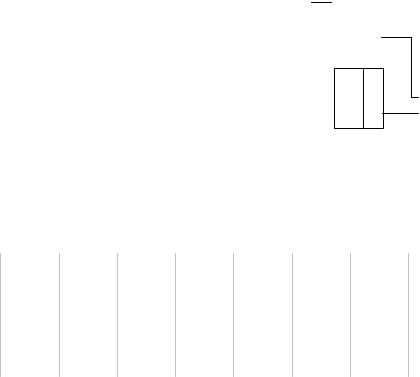
выявляющие большее или меньшее из двух сравниваемых многоразрядных двоичных чисел. Условное обозначение
такой |
схемы сравнения двух четырехразряд- |
|
|
|
A |
|
|
|
|
||
|
|
1 |
|
= = |
|
|
|
||||
|
|
|
|
|
|||||||
ных |
двоичных чисел приведено на рис. 5.15. |
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||
Четыре пары входов используются для приема |
|
|
4 |
|
A<B |
|
|
|
|||
|
|
|
|
|
|||||||
|
|
8 |
|
|
|
|
|||||
|
|
|
|
|
|
||||||
сравниваемых чисел А3А2А1А0 и В3В2В1В0. Вхо- |
|
|
|
|
|
|
|
|
|||
|
|
|
A<B |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
ды А<B, А=B и А>B предназначены для увели- |
|
|
|
A=B |
A=B |
|
|
|
|||
чения емкости схемы сравнения (соединения |
|
|
|
A>B |
A>B |
||||||
|
|
|
|||||||||
|
|
|
B |
|
|||||||
нескольких ИС при сравнении |
чисел с раз- |
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
рядностью n > 4). На выходах А<B, А=B и А>B |
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
4 |
|
|
|
|
|
|||
формируется логическая единица, если из двух |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
|
|
8 |
|
|
|
|
|
||||
сравниваемых чисел А и В А<В, |
А=В и А>В |
|
|
|
|
||||||
Рис. 5.15. |
Схема сравне- |
||||||||||
соответственно. |
|
ния четырехразрядных |
|||||||||
|
|
|
|||||||||
двоичных чисел
59
5.4.Преобразователи кода
Кпреобразователям кода (ПК) относятся цифровые схемы, осуществляющие преобразование входных слов { xn−1, xn−2 ,..., x0 } из одного
алфавита |
в выходные слова { ym−1, ym−2 ,..., y0} другого алфавита. Ус- |
|||||||
x0 |
|
|
|
|
|
|
y0 |
ловное графическое обозначение преобразователя |
|
1 |
|
x/y |
1 |
|
двоично-десятичного кода 8-4-2-1 в двоично- |
||
|
|
|
||||||
x1 |
|
2 |
|
|
2 |
|
y1 |
десятичный код 2-4-2-1 приведено на рис. 5.16. |
|
|
|
|
|||||
x2 |
|
4 |
|
|
4 |
|
y2 |
Для построения комбинационного преобразо- |
|
|
|
|
|||||
x3 |
|
8 |
|
|
2 |
|
y3 |
вателя кода необходимо располагать таблицей ис- |
|
|
|
|
|||||
Рис. 5.16. Условное |
тинности, в соответствии с которой синтезируется |
|||||||
обозначение преобра- |
многовыходная комбинационная схема, осуществ- |
|||||||
зователя кода 8-4-2-1 |
ляющая преобразование кода. Синтез подобных |
|||||||
|
в код 2-4-2-1 |
|
схем производится в соответствии с правилами, |
|||||
|
|
|
|
|
|
|
|
изложенными ранее. |
5.5. Шифраторы и дешифраторы
Шифраторы и дешифраторы являются частным случаем преобразователей кода.
Шифратором называется преобразователь кода 1 из N в двоичный код. Дешифратор реализует обратную функцию. Он является преобразователем двоичного n-разрядного кода в код 1 из N, где N = 2n.
Шифраторы. Синтез шифратора рассмотрим на примере преобразования кода 1 из 4 в двоичный код. Правила функционирования такого шифратора приведены в табл. 5.4. Непосредственно из нее следует: y0 =
= x1 + x3 и y1 = x2 + x3.
Схема шифратора, построенного в соответствии с этими формулами, и его условное обозначение приведены на рис. 5.17, а временные
диаграммы его сигналов – на рис. 5.18. |
|
|
|
|
|
|
|
||
Аналогичным |
образом синтезирует |
|
|
|
Таблица 5.4 |
||||
шифраторы кода 1 из n в любой другой |
|
|
|
||||||
Таблица истинности |
|
||||||||
код. |
|
|
|||||||
|
шифратора кода 1 из 4 |
|
|||||||
Дешифраторы. |
Дешифраторы по |
|
|
|
|
|
|
|
|
Номер |
x3 |
x2 |
x1 |
x0 |
y1 |
y0 |
|||
способу вывода информации подразделя- |
набора |
||||||||
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|||
ются на дешифраторы со стробированием |
|||||||||
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|||
и дешифраторы без стробирования, по ко- |
|||||||||
2 |
0 |
1 |
0 |
0 |
1 |
0 |
|||
личеству используемых выходов – на |
|||||||||
3 |
1 |
0 |
0 |
0 |
1 |
1 |
|||
полные и неполные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
60
