
- •ТЕМА I. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ.
- •§2.ЗАКОН КУЛОНА
- •§4 ЛИНИИ ВЕКТОРА НАПРЯЖЕННОСТИ. ПОТОК ВЕКТОРА НАПРЯЖЕННОСТИ.
- •§5 ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА.
- •§10 ОСНОВНАЯ ЗАДАЧА ЭЛЕКТРОСТАТИКИ.
- •§11 ПОЛЕ ЭЛЕКТРИЧЕСКОГО ДИПОЛЯ.
- •ТЕМА II. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ ПРИ НАЛИЧИИ ПРОВОДНИКОВ.
- •§12 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ЗАРЯЖЕННОГО ПРОВОДНИКА.
- •§15 КЛАССИФИКАЦИЯ ДИЭЛЕКТРИКОВ.
- •§ 21 СЕГНЕТОЭЛЕКТРИКИ.
- •ТЕМА V. СТАЦИОНАРНЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК.
- •§ 25. СИЛА И ПЛОТНОСТЬ ТОКА.
- •26. УРАВНЕНИЕ НЕПРЕРЫВНОСТИ.
- •§ 27. ЭКСПЕРИМЕНТАЛЬНЫЕ ЗАКОНЫ СТАЦИОНАРНОГО ТОКА.
- •§ 31. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ.
- •§ 32. ПРАВИЛА КИРХГОФА ДЛЯ ЛИНЕЙНЫХ РАЗВЕТВЛЕННЫХ ЦЕПЕЙ.
- •ТЕМА VI. МАГНИТНОЕ ПОЛЕ СТАЦИОНАРНОГО ТОКА В ВАКУУМЕ.
- •§ 38.КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ.
- •ТЕМА VII. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ.
- •§ 40. СВЯЗЬ МОЛЕКУЛЯРНЫХ ТОКОВ С ВЕКТОРОМ НАМАГНИЧИВАНИЯ.
- •ТЕМА VIII. НЕСТАЦИОНАРНОЕ МАГНИТНОЕ ПОЛЕ.
- •§ 44. ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.
- •§ 46. ЯВЛЕНИЕ САМОИНДУКЦИИ.
- •§ 47. ВЗАИМНАЯ ИНДУКЦИЯ.
- •§ 48 ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ.
- •ТЕМА IX. ЦЕПИ ПЕРЕМЕННОГО ТОКА.
- •§ 51. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С РАЗЛИЧНОЙ НАГРУЗКОЙ.
- •§ 53. ЭНЕРГИЯ И МОЩНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА.
- •§ 56 РЕЗОНАНС ТОКОВ.
- •§ 57.ТРЕХФАЗНЫЙ ТОК.
- •ТЕМА X. МАГНЕТИКИ
- •§ 58 МАГНИТОМЕХАНИЧЕСКИЕ ЯВЛЕНИЯ.
- •§ 59 ДИАМАГНЕТИЗМ. ЛАРМОРОВА ПРЕЦЕССИЯ.
- •§ 60 ПАРАМАГНЕТИКИ.
- •САМОСТОЯТЕЛЬНО: §61 ФЕРРОМАГНЕТИКИ.
- •ТЕМА XI. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- •§ 62 . ОБОБЩЕНИЯ МАКСВЕЛЛА. ТОК СМЕЩЕНИЯ.
- •§ 64. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ИХ СВОЙСТВА.
- •§ 66. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН.
- •§69.ОСНОВНЫЕ ПОНЯТИЯ ЗОННОЙ ТЕОРИИ ПРОВОДИМОСТИ ТВЕРДЫХ ТЕЛ.
- •§ 70 СОБСТВЕННАЯ И ПРИМЕСНАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ,
- •§ 71 РАБОТА ВЫХОДА. КОНТАКТНЫЕ ЯВЛЕНИЯ В МЕТАЛЛАХ.
- •§ 72 КОНТАКТ ПОЛУПРОВОДНИКОВ С РАЗЛИЧНЫМ ТИПОМ ПРОВОДИМОСТИ.
- •§ 73 ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ.
- •§ 74 ЭЛЕКТРОПРОВОДНОСТЬ ЖИДКОСТЕЙ.
- •§ 75 ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ.
- •§ 76 ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ.
- •§ 77 ПОНЯТИЕ О ПЛАЗМЕ.

РИС. 35 РИС.36
Напряжение (разность потенциалов) на всей батарее равно сумме напряжений на каждом конденсаторе, а заряды всех конденсаторов равны.
U = ∑Ui |
|
q |
= q |
2 |
= ... = q |
i |
= ... = q |
n |
|
|
||||||||||||||
|
i |
, |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Емкость батареи последовательно соединенных конденсаторов |
- это емкость такого конденсатора, которым, при этих |
|||||||||||||||||||||||
же напряжении и заряде, можно заменить всю батарею. |
|
|
|
|
|
|
|
|||||||||||||||||
U = |
q |
|
= ∑ |
q |
|
|
|
|
|
|
1 |
|
= ∑ |
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
C0 |
|
Ci |
|
|
|
||||||||||
|
C0 |
|
|
|
i Ci , |
|
|
|
|
i |
|
|
|
|||||||||||
При параллельном подключении конденсаторов (рис.36) соединяются между собой одноименно заряженные обкладки. |
||||||||||||||||||||||||
В этом случае суммарный заряд батареи равен сумме зарядов каждого конденсатора, а напряжение для всех одинаково: |
||||||||||||||||||||||||
q = ∑qi |
|
U =U |
|
=U |
|
|
= ... =U |
i |
= ... =U |
n |
||||||||||||||
|
i |
, |
|
1 |
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В этом случае емкость всей батареи можно заменить конденсатором с емкостью: |
||||||||||||||||||||||||
C0 |
|
|
q |
|
|
|
∑qi |
= ∑Ci |
C0 = ∑Ci |
|||||||||||||||
= |
|
= |
|
i |
|
|||||||||||||||||||
|
|
|
|
U |
|
|||||||||||||||||||
|
|
|
U |
|
|
|
|
|
|
i |
|
|
|
|
, |
|
|
|
|
i |
|
|
||
ТЕМА III. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ПРИ НАЛИЧИИ ДИЭЛЕКТРИКОВ.
§15 КЛАССИФИКАЦИЯ ДИЭЛЕКТРИКОВ.
97-98% всех диэлектриков можно разделить на три класса.
1.Неполярные диэлектрики, атомы и молекулы которых имеют такую конфигурацию электронных облаков, что центры «тяжести» положительных и отрицательных зарядов совпадают. В этом случае атомы и молекулы не имеют собственного дипольного момента.
К неполярным диэлектрикам относятся некоторые газы (напр., Не), жидкости (напр., бензол), сложные вещества (напр., парафин).
2.Полярные диэлектрики, это вещества, атомы и молекулы которых имеют такую конфигурацию электронных облаков, что центры «тяжести» положительных и отрицательных зарядов не совпадают. Атом или молекулу можно рассматривать как диполь и характеризовать определенным дипольным моментом. К полярным диэлектрикам относятся вода, спирт. Вне электрического поля молекулы – диполи ориентированы беспорядочно.
3.Ионные кристаллы можно рассматривать как систему двух подрешеток из положительных и отрицательных ионов.
§16 ДИПОЛЬ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ.
Диполь используется как модель для описания поведения молекул диэлектриков в электрическом поле.
Поэтому рассмотрим поведение диполя во внешнем электрическом поле. Для упрощения будем считать, что напряженность поля создаваемого самим диполем по сравнению с напряженностью внешнего поля очень мала, т.е. полем диполя можно пренебречь.
Рассмотрим жесткий диполь в однородном электрическом поле.
17

РИС.23 На заряды диполя со стороны поля действуют две равные по величине и противоположные силы, так называемая пара
сил, которая создает механический вращающийr момент (рис.23а).
F+ = F− = F Mr = [l × F ]= [l × qE]= [pr × E]
Так как поле потенциально, то работа сил поля идет на изменение энергии диполя:
dW = δA = Mdα = pE sinαdα W = −pE cosα + C = −( prE) + C
Если диполь расположен перпендикулярно линиям напряженности , то cos α=0 и энергия также равна нулю.
Если дипольный момент параллелен линиям напряженности, то энергия диполя в этом положении минимальна, а механический момент, действующий на диполь со стороны электрического поля, равен нулю (рис.23б).
Следовательно, положение, при котором диполь параллелен линиям напряженности – устойчивое, и свободный диполь в однородном электрическом поле будет располагаться вдоль линий напряженности.
Рассмотрим диполь в слабом неоднородном поле. В этом случае силы, действующие на заряды диполя, не равны.
|
|
r r |
r |
∂E |
|
|
|
F = qE+ − qE− = q(E+ − E_ ) |
E+ − E− = ∆E = |
|
l |
||
Результирующая этих сил : |
∂l |
|||||
, |
|
, |
||||
РИС.24 РИС.25
Под действием этих сил диполь будет поворачиваться, а его центр будет перемещаться в направлении результирующей силы.
МОЛЕКУЛЯРНАЯ КАРТИНА ПОЛЯРИЗАЦИИ ДИЭЛЕКТРИКОВ
Процессы, которые происходят в диэлектриках, помещенных в электрическое поле, рассматривают как три вида поляризации диэлектриков. Поляризацией диэлектрика называется явление ориентации или появления диполей под действием электрического поля.
1.Электронная или деформационная наблюдается для неполярных диэлектриков изза смещения (деформации) электронных облаков в электрическом поле (рис.37а).
18

а ) |
б) |
|
РИС.37 |
В результате этого у молекул или атомов возникает индуцированный дипольный момент, величина которого, как показывает опыт, пропорциональна напряженности
поля: pr = βEr, где β - поляризуемость молекулы.
2.Ориентационная или дипольная поляризация наблюдается для полярных диэлектриков, молекулы которых подобно жестким диполям способны ориентироваться вдоль линий напряженности поля, хотя этому препятствует тепловое движение
(рис.37б).
3.Ионной поляризацией называется смещение ионных подрешеток в кристаллических диэлектриках.
Представим диэлектрик в виде совокупности элементарных объемов, но содержащих настолько большое количество молекул, чтобы можно было ввести понятие температуры.
В результате поляризации элементарные объемы диэлектрика приобретают дипольные моменты, а на поверхности диэлектрика появляются связанные или поляризационные заряды.
Вектором |
|
поляризации или поляризованностью называется дипольный момент единичного объема. |
|||
r |
∑pri |
|
|
||
P = |
i |
|
, |
[Р]=Кл/м2 |
|
∆V |
|||||
|
|
|
|||
Поляризованность зависит от: химического состава и примесей, агрегатного состояния, от величины напряженности поля и от его направления по отношению к кристаллической решетке для анизотропных сред, от температуры и давления для дипольной поляризации.
а) |
б) |
в) |
РИС.38 На рис.38а показано появление поверхностных зарядов под действием внешнего поля. На рис.38б – ориентация диполей
диэлектрика вокруг положительно заряженного тела.
Если диэлектрик неоднородный, то при ориентировке диполей под действием внешнего поля внутри него появятся объемные заряды (весь диэлектрик при этом остается нейтральным). На рис.38в показано, что при этом число диполей в единице объема различно и в объеме, очерченном пунктирной линией присутствует объемный заряд.
17. ВЕКТОР ПОЛЯРИЗАЦИИ И СВЯЗАННЫЕ ЗАРЯДЫ.
Рассмотрим плоскопараллельный слой однородного изотропного диэлектрика находящийся в однородном электрическом поле, созданном в вакууме. Пусть вектор напряженности поля составляет угол Θ с нормалью. В однородном изотропном диэлектрике вектор поляризации будет направлен по вектору напряженности (рис.39).
19

РИС.39 РИС.40
Врезультате поляризации на гранях диэлектрика появятся поляризационные заряды с поверхностной плотностью :
σ′ = dqds′
Построим на ds цилиндр с образующими параллельными вектору напряженности. Цилиндр можно рассматривать как диполь с величиной дипольного момента : dp = dq′l = σ ′dsl
|
|
dp |
|
dp |
|
′ |
|
σ |
′ |
|
P = |
= |
= |
σ dsl |
= |
|
|||
|
dV |
hds |
l cos Θds |
cos Θ |
|||||
По определению модуль вектора поляризации: |
|
|
|
||||||
Следовательно: |
σ′ = P cos Θ = Pnr |
|
|
|
|
|
|
|
|
Поверхностная плотность связанных зарядов равна проекции вектора поляризации на направление нормали к поверхности диэлектрика. Физический смысл этой величины в том, что она равна величине заряда, который смещается через единичную площадку в направлении нормали к ней.
Если диэлектрик не однородный или электрическое поле не однородное, то поляризационные заряды могут появиться и
внутри его объема, причем ρ′ = ρ′(x, y, z).
Рассмотрим случай диэлектрика с неполярными молекулами, хотя полученные результаты будут справедливы для всех изотропных диэлектриков. Выделим некоторый объем в диэлектрике, ограниченный поверхностью S (рис.40).
Из рис.40 видно, что через те участки поверхности, где напряженность направлена вовнутрь, часть отрицательных зарядов покинет рассматриваемый объем, а через участки, где напряженность направлена наружу, в область войдет дополнительно отрицательный заряд.
Если вошедший и вышедший заряды не равны друг другу, то внутри области
′ |
|
|
|
|
|
′ |
появится объемный поляризационный заряд qv , а на ее поверхности – поверхностный поляризационный заряд qs . |
||||||
|
ρ′= |
dq′ |
qv |
= ∫∫∫ρ dV |
|
|
|
|
′ |
′ |
|
||
Введем объемную плотность поляризационных зарядов: |
|
dV |
, |
|
v |
r r |
|
|
′ |
|
′ |
||
|
qs = |
∫∫σ ds = ∫∫Pds |
||||
Весь заряд на поверхности можно рассчитать: |
|
|
|
S |
S |
|
Так как диэлектрик не имел избыточного заряда, то qV′ + q′S = 0
∫∫Pdsr = −∫∫∫ρ′dV = −q′
Следовательно:
Теорема Остроградского-Гаусса для вектора поляризации: поток вектора поляризации через любую замкнутую поверхность равен полному поляризационному заряду внутри этой поверхности, взятому с противоположным знаком.
В дифференциальной форме: divP = −ρ′ или P = −ρ′
Физический смысл этого выражения в том, что источниками линий вектора поляризации являются только связанные заряды. При поляризации диэлектрика поверхностные поляризационные заряды возникают всегда, а объемные поляризационные
заряды могут возникать только в неоднородных диэлектриках или в неоднородных полях.
20

§ 18. ТЕОРЕМА ОСТРОГРАДСКОГО – ГАУССА ДЛЯ ВЕКТОРА НАПРЯЖЕННОСТИ В ДИЭЛЕКТРИКАХ. ВЕКТОР ЭЛЕКТРИЧЕСКОГО СМЕЩЕНИЯ.
Поляризационные или связанные заряды также создают электрическое поле. Поэтому поле в диэлектрике – это результирующее поле свободных или сторонних (не имеющих отношения к диэлектрику) и связанных зарядов.
Теорема Остроградского-Гаусса для вектора напряженности в этом случае:
|
r |
|
|
|
1 |
|
|
|
|
|
|
q + q |
′ |
||||
∫∫Edsr = |
|
∫∫∫(ρ + ρ′)dV = |
|
||||||||||||||
|
|
ε |
|
|
|
||||||||||||
|
|
|
|
|
|
ε |
0 |
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
r |
ρ + ρ′ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
divE = |
|
|
|
|
|
|
Из теоремы в дифференциальной форме |
|
ε0 |
|
|
следует, что источниками линий напряженности |
||||||||||||
|
|
|
|
|
|||||||||||||
являются как свободные (сторонние) так и связанные заряды, |
распределение которых в веществе чаще всего неизвестно, и |
||||||||||||||||
из-за этого расчет вектора напряженности может быть невозможен. |
|
|
|
||||||||||||||
Преобразуем последнее выражение: |
|
|
|
|
|
||||||||||||
r |
ρ |
|
ρ′ |
|
|
|
ρ |
divP |
|
|
|
|
|
||||
divE = |
|
|
+ |
|
|
= |
|
|
− |
|
|
|
div(ε0 E + P)= ρ |
||||
ε0 |
ε0 |
ε0 |
ε0 , |
|
|||||||||||||
Если ввести |
вектор электрического смещения (индукции) |
|
D = ε0 E + P , то его величина и направление |
||||||||||||||
опредяляются не только вектором напряженности, но и вектором поляризации, т.е. связанными зарядами, а источниками |
|
линий этого вектора являются только свободные (сторонние) заряды: |
|
r |
r |
divD = ρ |
или ∫∫Dds = ∫∫∫ρdV = q . |
Теорема Остроградского-Гаусса для вектора смещения: поток вектора смещения через любую замкнутую поверхность равен суммарному свободному заряду внутри этой поверхности.
Следовательно, для расчета напряженности поля в диэлектриках, необходимо сначала определить вектор смещения, а затем рассчитать напряженность. [D]=Кл/м2
§ 19. ДИЭЛЕКТРИЧЕСКАЯ ВОСПРИИМЧИВОСТЬ И ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ.
Опытным путем установлено, что для однородных изотропных диэлектриков вектор поляризации: P = ε0 E ,
где (хи) - диэлектрическая восприимчивость, не зависящая от напряженности поля величина.
Для большинства диэлектриков эта величина порядка 1, но для воды она равна 80, а для спирта – 30.
Диэлектрическая восприимчивость зависит от: химического состава и примесей, |
агрегатного состояния и температуры |
||||||
для полярных диэлектриков. |
|
|
|
|
|
|
|
Рассмотрим |
электронную поляризацию. Как уже обсуждалось, |
в этом случае |
индуцированный дипольный момент |
||||
молекулы равен: |
pr = βEr |
Npr |
|
|
|
|
|
|
r |
|
NβE |
|
r |
||
|
P = |
|
= |
|
|
= nβE |
|
|
V |
V |
|
||||
Пусть в некотором объеме V содержится N молекул. Тогда: |
|
|
|
, т.е. диэлектрическая |
|||
восприимчивость |
зависит только от концентрации молекул, поляризуемости |
молекулы |
и не зависит от температуры |
||||
= nβ (рис.41 а)
При дипольной поляризации ориентации диполей препятствует тепловое движение и поляризуемость обратно пропорциональна абсолютной температуре (рис.41 б).
При наличии обоих типов поляризации график зависимости восприимчивости от температуры смещен (рис.41 с).
21
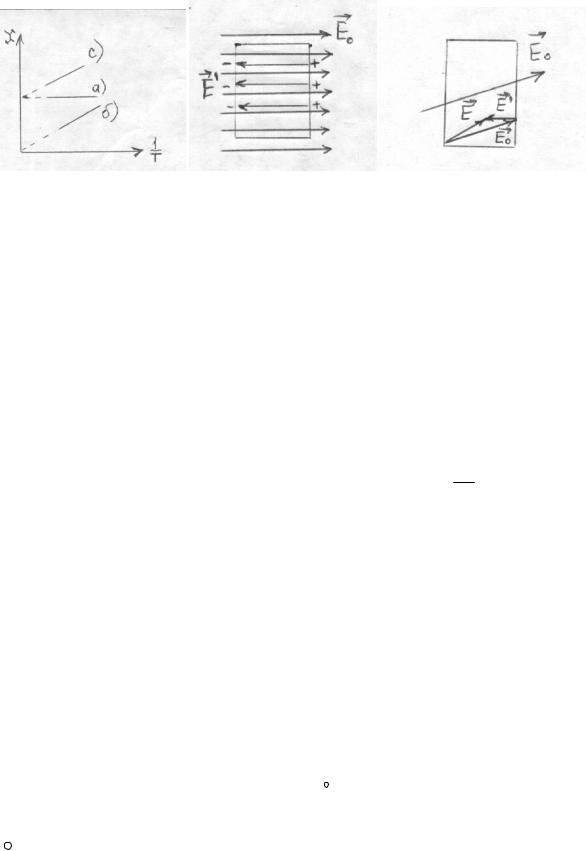
РИС.41 |
|
РИС.42 |
РИС.43 |
Получим выражение |
для вектора |
электрического смещения, используя связь между вектором поляризации и |
|
наrпряженностrи. |
r |
r |
|
D = ε0 E + P = ε0 E + ε0 E = ε0 (1+ )E = ε0εE |
|||
ε =1+ - относительная диэлектрическая проницаемость. |
|||
|
r |
r |
|
Формула связи |
D |
= ε0εE справедлива только для однородных изотропных диэлектриков и позволяет рассчитать |
|
напряженность поля по известным вектору смещения и диэлектрической проницаемости.
Рассмотрим плоскопараллельный слой однородного и изотропного диэлектрика, расположенного перпендикулярно линиям напряженности электрического поля, созданного в вакууме (рис.42).
Поляризационные заряды создают поле, направленное противоположно внешнему полю и тогда результирующее поле в диэлектрике равно:
|
|
′ |
|
σ ′ |
|
P |
|
|
E = E0 + E′, |
E = E0 − E |
= E0 |
− ε0 |
= E0 − ε0 |
= E0 − E , E0 = (1+ )E = εE |
|||
|
||||||||
Отсюда следует, что, в данном частном случае, диэлектрическая проницаемость – это число, показывающее во сколько раз напряженность поля в вакууме больше напряженности поля в диэлектрике: ε = EE0
Необходимо подчеркнуть, что это справедливо лишь при следующих условиях: 1)поле в вакууме и диэлектрике создается одними и теми же свободными зарядами, 2)диэлектрик однородный и изотропный,
3)диэлектрик безграничный или его поверхности совпадают с эквипотенциальными поверхностями внешнего поля. Если эти условия не выполняются, то данное соотношение не справедливо.
ПРИМЕР. Линии внешнего поля не перпендикулярны граням диэлектрика (т.е. грани не совпадают с эквипотенциальными поверхностями внешнего поля) как на рис.43.
Так как вектор напряженности поля поляризационных зарядов направлен перпендикулярно граням, то, в этом случае, напряженность результирующего поля в диэлектрике зависит не только от диэлектрической проницаемости и величины напряженности внешнего поля, но и от ее направления.
§ 20 ГРАНИЧНЫЕ УСЛОВИЯ.
Таким образом напряженность электрического поля меняется по величине и по направлению на границе вакуум – диэлектрик и, очевидно, будет изменяться на границе двух диэлектриков.
Рассмотрим границу раздела двух однородных изотропных диэлектриков, находящихся в однородном электрическом поле.
Пусть на границе раздела нет сторонних зарядов, нормаль направлена от первого диэлектрика ко второму, а вектор напряженности составляет с нормалью в первом диэлектрике угол Θ1, а во втором - Θ2.
критерий потенциальности электростатического поля ∫Edl = 0
Поскольку циркуляция вектора напряженности равна нулю по любому контуру, выберем замкнутый прямоугольный
контур 12341 так, чтобы d23→0 и d41→0. Тогда |
|||
r r |
r r |
r |
= E1 cos(90 −Θ1 )d12 − E2 cos(90 −Θ2 )= E1τ − E2τ = 0 |
∫Edl |
= ∫Edl |
+ ∫Edl |
|
|
12 |
34 |
|
Первое граничное условие: E1τ |
= E2τ |
||
22
