ТЕМА VIII. НЕСТАЦИОНАРНОЕ МАГНИТНОЕ ПОЛЕ.

§ 44. ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.

Связь магнитного поля с протекающим в проводнике током обусловила эксперименты по возбуждению тока в проводящем контуре с помощью магнитного поля. Эта задача была решена в 1831 г. английским физиком Майклом Фарадеем.

Явление электромагнитной индукции – в замкнутом проводящем контуре при всяком изменении магнитного потока через поверхность, охватываемую контуром, возникает индукционный магнитный ток.

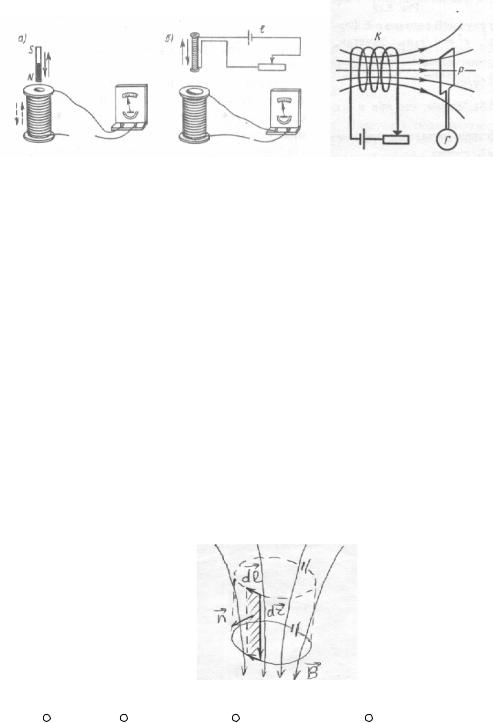
Суть классических опытов Фарадея представлена на рис.104-105. Магнитный поток через витки катушки, присоединенной к чувствительному гальванометру, можно изменять как взаимным перемещением постоянного магнита и катушки(рис.104а), так и перемещением одной катушки с током в магнитном поле другой катушки (рис.104б).

В обоих случаях возникает индукционный ток, но его направление определяется тем, убывает магнитный поток или возрастает. На рис.105 изменение магнитного потока через поверхность контура вызывается изменением тока в катушке с помощью реостата, включенного в цепь катушки.

Появление индукционного тока в проводнике означает, что при изменении магнитного потока через поверхность, им ограниченную, возникает фактор, который обеспечивает направленное движение зарядов. По аналогии с цепями постоянного тока можно ввести ЭДС индукции.

Фарадей установил, что ЭДС индукции совершенно не зависит от того, каким образом изменяется магнитный поток, и определяется лишь скоростью изменения магнитного потока, а в 1845 г. Ф.Э.Нейман ввел математическую запись закона

Знак (-) в законе соответствует эмпирическому правилу Э.Х.Ленца: индукционный ток всегда направлен так, что создаваемое им магнитное поле противодействует изменению магнитного потока, вызвавшего появление индукционного тока.

Возникновение ЭДС индукции в контуре, перемещающимся под действием магнитного поля, было впервые обосновано Гельмгольцем в 1894 г. на основании закона сохранения энергии.

Рассмотрим замкнутый на источник контур общим сопротивлением R. Если контур неподвижен и нет преобразований в другие виды энергии, то работа источника за некоторое время, по закону Джоуля-Ленца, равна количеству теплоты

выделяющейся в контуре за это время: A = Q = I 2 Rt .

Пусть в некоторый момент в пространстве, где расположен контур, возникает неоднородное магнитное поле (рис.106). В представленном случае под действием магнитного поля контур начнет втягиваться в область более сильного поля, а следовательно, за малый промежуток времени dt поток через площадь контура изменится от Ф0 до Фt.

По закону сохранения энергии: εIdt = I 2 Rdt +δA , где δA - работа по перемещению контура за это время. Рассчитаем величину той работы как сумму работ по перемещению малых элементов

контура под действием силы Ампера.

боковую часть указанной на рисунке замкнутой поверхности. По теореме о полном магнитном потоке:

48

Это выражение показывает, что сила тока в цепи обусловлена и источником постоянной ЭДС и ЭДС индукции, которая определяется аналогично установленному экспериментально закону электромагнитной индукции.

§ 45 ПРИРОДА СТОРОННИХ СИЛ ПРИ ЯВЛЕНИИ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.

Опыты, в которых проявляется явление электромагнитной индукции можно разделить на две группы. Появление индукционного тока наблюдается в проводниках, движущихся в магнитном поле, а также индукционный ток возникает в неподвижных проводниках, находящихся в переменном магнитном поле.

I. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ. При движении проводника (и зарядов внутри него) в магнитном поле (рис.107), в качестве сторонней силы выступает сила Лоренца, под действием которой возникает

направленное движение электронов. FΛ = qV ×B = FCΤ

Таким образом ЭДС индукции обусловлена магнитным потоком через поверхность, «покрываемую» или «заметаемую» проводником при его движении в магнитном поле(рис.109).

49

Возникновение индукционного тока означает, что, в этом случае, внутри проводника возникает электрическое поле, действием которого обусловлено направленное движение зарядов.

Впервые к такому выводу пришел Дж.Максвелл, который предположил, что нестационарное магнитное поле порождает

rotErB = − ∂∂Bt .

Физический смысл последнего выражения в том, что «вихри» переменного электрического поля охватывают вектор скорости изменения магнитной индукции в соответствии с правилом «левого» винта.

Вихревое электрическое поле всегда возникает в пространстве, в котором существует нестационарное магнитное поле. Замкнутый проводник с возникающим индукционным током играет роль зонда, позволяющего обнаружить вихревое электрическое поле.

Рассмотрим примеры проявления индукционных токов.

ПРИМЕР 1. Опыт показывает, что если вихревое электрическое поле возникает в сплошных металлических проводниках, то, в них также появляются индукционные токи, называемые токами Фуко по имени первого их исследователя. В общем случае распределение этих токов в проводнике может быть очень сложным. На рис.110 показаны токи Фуко возникающие в соленоиде с переменным током.

Как и все индукционные токи, токи Фуко подчиняются правилу Ленца, и поэтому тормозящее действие индукционных токов используется для «успокоения» (демпфирования) подвижных частей различных приборов.

ПРИМЕР 2. Из-за малого сопротивления сплошных проводников, при протекании индукционных токов может выделяться большое количество тепла, что используется в индукционных металлургических печах. Для предотвращения таких тепловых потерь якоря генераторов и сердечники трансформаторов делают не сплошными, а собирают из изолированных друг от друга тонких пластин.

ПРИМЕР 3. При протекании переменного тока по проводам также возникают индукционные токи, которые всегда противодействуют изменению первичного тока внутри проводника.

И при возрастании тока (рис.111) и при убывании (рис.112) вследствие возникновения индукционных токов переменный ток оказывается распределенным по сечению проводника неравномерно – он как бы вытесняется на поверхность проводника. Это явление называется скин-эффектом (от англ. skin – кожа), или поверхностным эффектом. Поскольку токи высокой частоты текут в тонком поверхностном слое, то провода для них могут быть полыми.

ПРИМЕР 4. При нагревании сплошных проводников токами высокой частоты, в результате skin-эффекта происходит нагревание только их поверхностного слоя, что лежит в основе метода поверхностной закалки металлов. Варьируя частоту, можно производить закалку на любой требуемой глубине.

§ 46. ЯВЛЕНИЕ САМОИНДУКЦИИ.

Как уже обсуждалось, явление электромагнитной индукции наблюдается при всяком изменении магнитного потока независимо от причины, вызвавшей это изменение.

Если в некотором контуре течет изменяющийся во времени ток, то изменяется магнитное поле этого тока, а, следовательно, магнитный поток через поверхность, ограниченную контуром.

Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется явлением самоиндукции.

Магнитный поток, обусловленный собственным током контура (сцепленный с контуром), пропорционален магнитной индукции, которая, в свою очередь, по закону Био-Савара-Лапласа, пропорциональна току.

50

Φ = LI , где L –коэффициент самоиндукции или индуктивность, «геометрическая» характеристика проводника, так как зависит от его формы и размеров, а также от магнитных свойств среды.

[L]=1 Гн=1Вб/1А.

При изменении силы тока изменяется и сцепленный с контуром поток, а следовательно возникает ЭДС самоиндукции. Если контур жесткий, ферромагнетики отсутствуют, распределение и магнитные свойства вещества среды неизменны,

Индуктивными свойствами обладают любые реальные проводники, но величина индуктивности наибольшая для соленоида, поэтому явление самоиндукции наиболее сильно проявляется в цепях, содержащих эти элементы.

Замкнем цепь, содержащую источник постоянной ЭДС, соленоид и сопротивление (рис.113).

Как уже обсуждалось, ЭДС индукции появляется при любом изменении магнитного потока, независимо от причины, вызывающей это изменение. Тогда, в соответствии с законом сохранения энергии, ток в цепи определяется как источником,

Следовательно, ток в цепи устанавливается не мгновенно, а возрастая по экспоненциальному закону до стационарного значения (рис.114).

При размыкании этой цепи сила тока также, по экспоненциальному закону, убывает в течение некоторого времени:

При большой величине индуктивности и малом времени размыкания цепи токи самоиндукции могут достигать очень большой величины, поэтому существует термин «экстратоки» самоиндукции.

51