13. Проблемы гетероскедастичности модели. Критерии ее диагностики.

Проблема гетероскедастичности возникает, когда точность наблюдений, проведенных в различные моменты времени, неодинакова, другими словами:

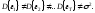
Различают явную и неявную гетероскедастичность. Явная гетероскедастичность возникает, когда шоковая переменная модели имеет различные дисперсии в различные моменты наблюдения правильно специфицированной модели.

Неявная гетероскедастичность возникает вследствие неправильной спецификации модели.

последствия гетероскедастичности:

1. Неявный тип гетероскедастичности является причиной смещения оценок параметров модели.

2. Дисперсия оценок параметров возрастает, что означает меньшую их значимость.

3. Возникает эффект недооценки величины дисперсии МНК-оценок параметров, поскольку средствами t и F-критерия не удается распознать эту проблему.

1. Критерий Парка (Park).

Шаг 1. С помощью МНК оценивают параметры модели и рассчитывают отклонения:

Шаг 2. Применяют полученные отклонения 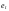для построения вспомогательной модели, оценивающей:

,

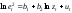где

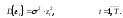
Шаг 3. Производят проверку значимости параметров вспомогательной модели по критерию Стьюдента. При получении вывода о значимости параметров диагностируют наличие гетероскедастичности.

2. Критерий Голдфелда-Кандта (Goldfeld-Quandt).

Шаг 1. Упорядочивают наблюдения над эндогенной переменной в соответствии с величиной фактора z:

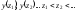
Шаг 2. Разбивают выборку на 3 части объемами: 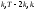Образуют вспомогательную регрессию, образованную из 1-й и 3-й частей упорядоченной выборки, рассчитывают остатки:RSS(3), RSS(1).

Шаг 3. Применяют F-критерий с решающей функцией вида:

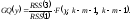
Если расчетное значение величины 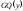превышает табличное, то делают вывод о наличии гетероскедастичности.

3. Критерий Бриша-Пагана (Breusch-Pagan).

Шаги 1 и 2 совпадают с критерием Парка, где учитывают _.

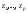Шаг 3. Гипотезу значимости параметров вспомогательной регрессии 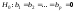осуществляют на основе решающей функции:

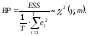
Если расчетное значение статистики ВР превышает табличное значение из таблиц 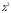-Пирсона, то делают вывод о наличии гетероскедастичности.

Четвертый критерий, хотя и относительно трудоемкий, но не требует задания фактора пропорциональности

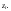
4. Критерий Вайта (White).

Шаг 1. Вычисляют остатки исходного эконометрического уравнения

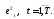
Шаг 2. Образовывают вспомогательную модель:

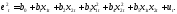
Шаг 3. Осуществляют МНК-оценивания регрессии, полученной на предыдущем шаге и проверяют значимость ее параметров по пра-вилу:

,

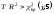где 5 – число экзогенных переменных, исключая константу.

При подтверждении данного неравенства делают вывод о наличии гетероскедастичности.

Основным методом, позволяющим производить оценивания и принимать решения по эконометрическим моделям, функционирующим в рамках гетероскедастичности, является взвешенный (обобщенный) МНК. Приведем его описание для случая множественной регрессии с двумя экзогенными переменными.

Пусть модель такова, что

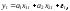
где 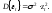Причем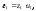где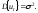

Тогда, преобразуя модель следующим образом:

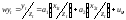
приходим к модели с отсутствием гетероскедастичности.

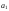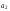Далее оценивают параметры ипо классическому МНК на основе преобразованных переменных: