18. Модели с распределенными лагами: структура лагов по Койку: Частные случаи (модель с неполной корректировкой и адаптивных ожиданий)

модель с распределённым лагом - это модель временного ряда, в которой в уравнение регрессии включено как текущее значение объясняющей переменной, так и значения этой переменной в предыдущих периодах.

Лаговые переменные – переменные, влияние которых характеризуется определенным запаздыванием. Это модели, содержащие в качестве лаговых переменных лишь независимые переменные.

Простейший пример модели с распределённым лагом:

В более общем случае:

Здесь можно говорить о краткосрочном воздействии объясняющей переменной на объясняемую , а также о долгосрочном.

Данная модель, в свою очередь, является частным случаем Модели авторегрессии и распредёленного лага.

Примеры макроэкономических моделей, в которых важен временной лаг:

• функция потребления;

• создание денег в банковской системе;

• связь между денежной массой и уровнем цен;

• лаг между расходами на НИОКР и производительностью;

• "кривая джей" (J-curve) связи между валютным курсом и торговым балансом;

• модель акселератора инвестиций.

Причин наличия лагов в экономике достаточно много, и среди них можно выделить следующие:

• Психологические причины – обычно выражаются через инерцию в поведении людей. Например, люди тратят свой доход постепенно, а не мгновенно. Привычка к определенному образу жизни приводит к тому, что люди приобретают те же блага в течение некоторого времени даже после падания реального дохода.

• Технологические причины – например, изобретение персональных компьютеров не привело к мгновенному вытеснению ими больших ЭВМ в силу необходимости замены соответствующего программного обеспечения, которое потребовало продолжительного времени.

• Институциональные причины – например, контракты между фирмами, трудовые договоры требуют определенного постоянства в течение времени контракта.

• Механизм формирования экономических показателей – например, инфляция во многом является инерционным процессом, денежный мультипликатор также проявляет себя на определенном временном интервале.

Основную сложность для эмпирической оценки модели с распределённым лагом представляет наличие мультиколлинеарности, т.к. в экономических данных соседние значения одного и того же ряда данных обычно высоко коррелированы друг с другом. Кроме того, не всегда возможно априори определить, сколько лаговых переменных стоит включать в модель. Существуют даже модели с бесконечным числом лаговых регрессов, коэффициенты при которых бесконечно уменьшаются (например, в геометрической прогрессии). Существует множество специальных технологий для работы с распределенными лагами: так, метод Тинбергена и Альта представляет собой "метод большого пальца" для определения оптимального числа лаговых переменных, не внося дополнительных предпосылок в модель. Модели Койка и Алмон, напротив, вводят предпосылки относительно лаговых коэффициентов, позволяющие упростить их оценку.

Подход Тинбергена и Альта

Подход Тинбергена и Альта позволяет нащупать баланс между точностью модели (числом включенных лаговых переменных) и качеством оценки (мультиколлинеарностью). Он предполагает последовательную оценку моделей:

Остановка процесса рекомендуется, когда какой-либо из коэффициентов при лаговых переменных меняет знак или становится статистически незначимым, что является следствием возникновения мультиколлинеарности. Кроме того, маловероятна, но возможна такая ситуация, когда просто не будет достаточно наблюдений для дальнейшего увеличения числа лаговых переменных.

Преобразование Койка

Преобразование Койка — приём, позволяющий оценить модель с распределёнными лагами путём простого предположения о том, что коэффициенты при лаговых переменных убывают в геометрической прогрессии с увеличением лага:

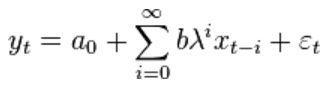
В этой модели несложно найти средний лаг , а также медианный лаг.

Вычтя из данного уравнения уравнение для ,умноженное на, получаем простую модель:

Эта модель легко может быть оценена обычным методом наименьших квадратов без потери степеней свободы. Здесь, однако, существует автокорреляция случайного члена с, и, что хуже, случайный член коррелирует с объясняющей переменной. Поэтому для оценки модели рекомендуется использовать метод инструментальных переменных или оценивать исходную модель с помощью нелинейного метода наименьших квадратов.

Преобразование Койка иллюстрирует взаимосвязь моделей с распределённым лагом и авторегрессионных моделей. Модели Койка соответствуют два широко применяемых теоретических подхода к распределённым лагам: модель адаптивных ожиданий и модель частичной подстройки.

Модель адаптивных ожиданий

Предполагается, что зависимая переменная является функцией от ожидаемого значения объясняющей переменной. Это характерно, например, для моделей инфляции.

Ожидания же формируются как средневзвешенное из предыдущих ожиданий и текущего значения переменной:

Алгебраические манипуляции приводят к построению модели, по форме совпадающей с моделью Койка:

Модель частичной подстройки

Модель частичной подстройки предполагает наличие долгосрочной зависимости:

Это характерно, например, для моделей экономического роста, где потенциальный выпуск определяется спросом. Однако объясняемая переменная не может моментально подстроиться под изменения объясняющей:

Таким образом, принципиальное различие моделей частичной подстройки и адаптивных ожиданий состоит в том, какая переменная изменяется не мгновенно: объясняемая или объясняющая. Однако функциональная форма у них схожая: после преобразований, получим

Можно заметить, что здесь, в отличие от модели адаптивных ожиданий, нет корреляции ошибок друг с другом и с объясняющей переменной. Однако выбор модели, конечно, должен объясняться не удобством её оценки, а теоретическими предпосылками, лежащими в основе исследуемого явления.

ЕЩЕ РАЗ

Модель адаптивных ожиданий

Ожидания играют весьма существенную роль в экономической активности. Этот факт в определенной мере затрудняет моделирование соответствующих экономических процессов, ведь измерение и моделирование является весьма сложной задачей. Одним из направлений решения такой задачи является модель адаптивных ожиданий. В данной модели происходит постоянная корректировка ожиданий на основе получаемой информации ореалезации исследуемого показателя. Если реальное значение показателя оказалось больше ожидаемого, то ожидаемое в следующем периоде значеине корректируется в сторону увеличения, в противном случае- наоборот. При этом величина корректировки должна быть пропорциональна разности между реальным и ожидаемым значениями.

В данной модели в уравнение регрессии в качестве объясняющей переменной вместо текущего значения х_t входит ожидаемое (долгосрочное) значение х⃰_t:

y_t = α + βx_t + ε_t (1)

Так как ожидаемые значения не являются фактически существующими, выдвигается предположение, что эти значения связаны следующим соотношением:

x⃰t− x⃰t−1= γ (x t− x⃰t−1) .

(2)

Именно модель (2) известна как модель адаптивных ожида-

ний. Коэффициент 0≤ γ ≤ 1 называетсякоэффициентом ожидания.

Иногда в модели (12.14) вместо текущего значения xt используют предыдущее xt-1:

x⃰t− x⃰t−1= γ (x t−1− x⃰t−1) .	(3)
Уравнение (2) можно переписать в виде
x⃰t = γ xt + (1− γ)xt−1 .	(4)

Из (4) видно, что ожидаемое значение x⃰_t является взвешенным средним между текущим значением x_t и его ожидаемым значением в предыдущий период с весами γ и (1− γ) соответственно. Если γ =0, то ожидания являются неизменными (статичными): x⃰_t = x⃰_t−1 . Если γ = 1, то x⃰_t = x_t, что означает мгновенно реализуемые ожидания. Подставив соотношение (4) в (1), получим:

yt = α + β (γ хt + (1− γ)x⃰t−1 )+ еt .

(5)

Вычитая из (5) аналогичное уравнение для yt−1, умноженное на (1− γ), получим:

yt − (1− γ ) yt-1 = γ α + γ β xt + (еt − (1− γ)е t −1) .
yt = γ α + γ β xt + (1− γ)yt −1 + υt ,	(6)

где υ_t =ε_t − (1− γ)ε _t−1.

Из (1) очевидно, что коэффициент β определяет величину изменения в среднем текущего значения y_t при изменении ожидаемого значения x⃰_t на единицу. По уравнению (6) при изменении текущего значения x_t на единицу значение y_t меняется в среднем наβγ. Эти коэффициенты пропорциональности будут равны лишь при γ = 1, т. е. когда текущее и ожидаемое в долгосрочном периоде значения СВ Х совпадают (x⃰_t = x_t).

На практике при оценивании параметров авторегрессионного уравнения (6) вначале оценивается параметр γ (коэффициент прилаговом значении y), а затем коэффициент при xt (β=βγ/γ) и свободный член (α = α γ/ γ)

Этот же вывод можно обосновать, если предположить, что зависимая переменная yt в текущий момент времени связана с ожидаемым в следующий период времени значением x⃰_t+1 объясняющей переменной соотношением yt = α + βx⃰t+1 + еt (7)

В этом случае желательно выразить yt через реальные текущие и предыдущие значения объясняющей переменной Х. Для этого можно воспользоваться соотношением, аналогичным (4), предположив, что ожидаемое в следующий период времени значение переменной определяется как взвешенное среднее ее реального и ожидаемого значений в текущий период времени:

x⃰t+1 = γ xt + (1− γ)x⃰t .

(8)

Воспользовавшись этим же соотношением для ожидаемого значения xt , получим:

x⃰t +1 = γ xt + (1− γ) [γ xt −1 + (1− γ )x⃰t −1] =

= γ xt + γ(1− γ)x_t−1 + (1− γ)² x⃰_{t−1 .}

Продолжив процедуру использования соотношения (4) для x⃰t −1 , затем для x⃰t −2 и так до бесконечности, получим:

x⃰t +1 = γ [xt + (1− γ )xt −1 + (1− γ )2x⃰t −2 + ...].	(9)
Подставив полученное x t+1 в (7), имеем:
yt = α + βγ[xt + (1− γ)xt −1 + (1− γ)2 x⃰t −2+ ...]+ еt .	(10)

Обозначив βγ черезβ0 и (1− γ) черезλ, получаем соотношение

yt =α +β0 xt +β0λxt−1 +β0λ2xt−2 + ... +εt,

к которому можно применить преобразование Койка.

Модель адаптивных ожиданий может использоваться при анализе зависимости потребления от дохода, спроса на деньги либо инвестиций от процентной ставки и в других ситуациях, где экономические показатели оказываются чувствительными к ожиданиям относительно будущего.

Модель частичной корректировки

Вмодели частичной корректировки (модели акселератора) в

уравнение регрессии в качестве зависимой переменной входит не фак-

тическое значение yt, а желаемое (долгосрочное) значение y⃰t :

y⃰t =α +βxt +εt.

(1)

Так как гипотетическое значение yt не является фактически существующим, то относительно его выдвигается предположениечас-

тичной корректировки:

yt − yt−1 =λ( y⃰t − yt−1),

(2)

по которому фактическое приращение зависимой переменной yt − yt−1пропорционально разнице между ее желаемым значением и значением в предыдущий период y⃰t − yt−1. 0≤ λ ≤ 1− коэффициент корректи-

ровки. Уравнение (2) преобразуется к следующему виду:

yt =λy⃰t + (1− λ)yt−1.	(3)
Подставив (1) в (3), получим следующую модель
yt =λα +λβ xt + (1− λ)yt−1 +λεt,	(4)

которая называется моделью частичной корректировки. Из (3)

видно, что текущее значение yt является взвешенным средним желаемого уровня y⃰t и фактического значения данной переменной в предыдущий период. Чем большеλ, тем быстрее идет корректировка. Приλ = 1 полная корректировка происходит за один период. Приλ = 0 корректировка не происходит вовсе.

Таким образом, в уравнении (1) определяется долгосрочное (желаемое) значение y⃰ переменной Y (иногда под y⃰ понимается равновесное значение). Можно сказать, что в уравнении (4) определяется краткосрочное значение yt переменной Y, которое далеко не всегда совпадает с долгосрочным. Однако, определив коэффициенты регрессии уравнения (4) (вначалеλ, стоящее при yt−1, затем β= λβ/β и α= λα/ λ), мы тем самым оцениваем параметры уравнения (1).

Модель частичной корректировки (4) аналогична модели Койка. Она также включает в себя случайную объясняющую переменную yt−1. Но в данной модели эта переменная не коррелирует с текущим значением случайного отклоненияεt (т. к.εt рассчитывается после того, как определилось значение yt−1). В этом случае МНК позволяет получить асимптотически несмещенные и эффективные оценки.