
- •1. Основные понятия математического моделирования социально-экономических систем
- •2. Предмет, цель и задачи эконометрики. Эконометрическая модель, основные этапы построения эконометрической модели.
- •Этапы эконометрического моделирования:
- •3. Простая (парная) линейная регрессия (плр). Классические предположения моделей.
- •Классические модельные предположения
- •4. Статистическое оценивание параметров плр по методу наименьших квадратов. Свойства мнк – оценок
- •Свойства мнк-оценок:
- •5. Проверка качества множественной линейной регрессии: значимость параметров, доверительные интервалы, адекватность модели. Прогнозирование.
- •6. Множественная линейная регрессия (млр). Классические предположения. Мнк-оценка параметров модели.
- •7. Свойства мнк-оценок множественной линейной регрессии. Теорема Гаусса- Маркова.
- •8. Проверка качества множественной линейной регрессии: значимость параметров, доверительные интервалы, адекватность модели. Прогнозирование.
- •5. Коэф. Детерминации
- •Прогнозирование по модели множественной линейной регрессии
- •9. Спецификация эконометрической модели: способы и диагностика отбора экзогенных переменных. Тесты Рамсея и Амемья.
- •Критерий Рамсея (Ramsey):
- •10. Спецификация эконометрической модели: выбор формы зависимости нелинейной модели
- •Принципы спецификаций
- •11. Проблема наличия мультиколлинеарности. Последствия наличия и диагностики мультиколлинеарности.
- •Методы диагноза мультиколлинеарности:
- •12. Методы устранения мультиколлинеарности. Метод главных компонент. Гребневая регрессия.
- •13. Проблемы гетероскедастичности модели. Критерии ее диагностики.
- •1. Критерий Парка (Park).
- •2. Критерий Голдфелда-Кандта (Goldfeld-Quandt).
- •3. Критерий Бриша-Пагана (Breusch-Pagan).
- •4. Критерий Вайта (White).
- •14. Обобщенный мнк (омнк). Свойства оценок млр по омнк. Взвешенный мнк в задаче оценивания параметров модели. Свойства оценок по взвешенному мнк.
- •Вопрос 15. Проблема автокорреляции остатков модели. Последствия автокорреляции при использовании модели.
- •Причины автокорреляции остатков
- •Последствия автокорреляции:
- •16. Критерий диагностики автокорреляции Дарбина-Уотсона
- •17.Методы устранения автокорреляции. Процедуры оценивания Кохрейна-Оркатта и Хильдрета-Лу
- •18. Модели с распределенными лагами: структура лагов по Койку: Частные случаи (модель с неполной корректировкой и адаптивных ожиданий)
- •19 Модели с распределенными лагами: линейно-арифметическая структура лагов и полиномиальная структура лагов по Алмон
- •20. Тест h-Дарбина и множественный тест Лагранжа проверки автокорреляции в лаговых моделях
- •21. Понятие временного ряда (вр). Модель вр, основные задачи анализа вр. Методы сглаживания вр (скользящего среднего, экспоненциального сглаживания, последовательных разностей)
- •22 Стационарность временного ряда (вр). Характеристики корреляции уровней вр.
- •23 Стационарные модели временных рядов: авторегрессии, скользящего среднего, арсс
- •24. Нестационарная модель арисс. Оценка параметров модели.
- •28. Прогнозирование временных рядов. Показатели точности прогнозов.
- •30. Тест Чоу диагностики включения фиктивных переменных в эконометрическую модель.
- •32. Системы одновременных эконометрических уравнений (соу). Структурная и приведенная форма соу (графическое и матричное представление).
- •33. Проблемы идентификации систем одновременных уравнений (соу). Идентифицируемость уравнений соу (порядковый и ранговый критерии)
- •34. Методы оценивания систем одновременных уравнений: косвенный мнк, двухшаговый мнк. Применимость и свойства оценок
- •35. Современное состояние эконометрики. Примеры больших эконометрических моделей
11. Проблема наличия мультиколлинеарности. Последствия наличия и диагностики мультиколлинеарности.
Если
имеется линейная
связь экзогенных переменных,
например
 ,
то МНК-оценки не будут существовать,
т.к. не существует обратная к матрице
,
то МНК-оценки не будут существовать,
т.к. не существует обратная к матрице ,
которая будет вырожденной. Такая ситуация
в эконометрике носит название проблемымультиколлинеарности.
,
которая будет вырожденной. Такая ситуация
в эконометрике носит название проблемымультиколлинеарности.
Причины мультиколлинеарности:
неправильная спецификация модели
небрежное проведение сбора статданных (использование повторных наблюдений).
Различают явную и неявную мультиколлинеарность.
Явная – известна точная линейная зависимость между переменными модели.
Например, если в модель инвестиционного процесса включить номинальную и реальную процентные ставки, т.е.

где
известна зависимость реальной и
номинальной ставок и темпа инфляции


то имеет место явная мультиколлинеарность.
Неявная возникает, когда существует стохастическая (неопределенная, случайная) линейная зависимость между экзогенными переменными.
преобладает неявная, ее наличие характеризуют 6 признаков:
1. МНК-оценки параметров модели теряют свойства несмещенности.
2. Дисперсия МНК-оценок возрастает:

Вследствие
того, что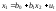 ,
коэффициент корреляции
,
коэффициент корреляции ,
тогда
,
тогда ,
что влечет
,
что влечет
3. Происходит уменьшение t-статистик, являющихся индикаторами значимости параметров:
4. Коэффициент детерминации уже не является мерой адекватности модели, так как низкие значения t-статистик влекут недоверие к подобранной модели зависимости.
5. Оценки параметров при неколлинеарных экзогенных переменных становятся очень чувствительными к изменению данных.
6. Оценки параметров при неколлинеарных экзогенных переменных становятся незначимыми.
Методы диагноза мультиколлинеарности:
Визуальный метод, который основан на факте, что уровень значимости всего уравнения
 значительно меньше указывает на наличие
мультиколлинеарности, чем уровни
значимости индивидуальных экзогенных
переменных
значительно меньше указывает на наличие
мультиколлинеарности, чем уровни
значимости индивидуальных экзогенных
переменных .
.Высокое значение коэффициента парной корреляции входящих в модель экзогенных переменных
 (в примере
(в примере ).
).Метод инфляционных факторов, который по трудоемкости доступен реализации только с помощью компьютерных прикладных программ.
Шаг 1. В модели (исходной) множественной линейной регрессии переберем все подмодели, в которых какая-либо экзогенная переменная становится эндогенной, т.е.
 .
.

Шаг
2. Вычисляем
коэффициенты детерминации всех полученных
моделей
 ,
на основе которых рассчитаем так
называемые инфляционные факторы:
,
на основе которых рассчитаем так
называемые инфляционные факторы:
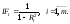
Если
 ,
то делают вывод о существовании
мультиколлинеарности.
,
то делают вывод о существовании
мультиколлинеарности.
Рекомендации, уменьшающие влияние мультиколлинеарности:
а) в модели не изменяют никакую структуру, а, применяя компьютерный МНК, анализируют наличие проблемы мультиколлинеарности по визуальным методам.
б) улучшают спецификацию модели, устраняя из исходной модели коллинеарные экзогенные переменные.
в) увеличивают объем статистических данных.
г) объединяют коллинеарные переменные и включают в модель общую экзогенную переменную.
12. Методы устранения мультиколлинеарности. Метод главных компонент. Гребневая регрессия.
Если основная задача модели − прогноз будущих значений зависимой переменной, то при достаточно большом коэффициенте детерминации R2 (≥ 0.9) наличие мультиколлинеарности зачастую не сказывается на прогнозных качествах модели.
Если целью исследования является определение степени влияния каждой из объясняющих переменных на зависимую переменную, то наличие мультиколлинеарности исказит истинные зависимости между переменными. В этой ситуации мультиколлинеарность представляется серьезной проблемой.
Отметим, что единого метода устранения мультиколлинеарности, годного в любом случае, не существует. Это связано с тем, что причины и последствия мультиколлинеарности неоднозначны и во многом зависят от результатов выборки.
МЕТОДЫ:
Исключение переменной(ых) из модели
Например, при исследовании спроса на некоторое благо в качестве объясняющих переменных можно использовать цену данного блага и цены заменителей данного блага, которые зачастую коррелируют друг с другом. Исключив из модели цены заменителей, мы, скорее всего, допустим ошибку спецификации. Вследствие этого возможно получение смещенных оценок и осуществление необоснованных выводов. в прикладных эконометрических моделях желательно не исключать объясняющие переменные до тех пор, пока коллинеарность не станет серьезной проблемой.
Получение дополнительных данных или новой выборки
Иногда достаточно увеличить объем выборки. Например, при использовании ежегодных данных можно перейти к поквартальным данным. Увеличение количества данных сокращает дисперсии коэффициентов регрессии и тем самым увеличивает их статистическую значимость. Однако получение новой выборки или расширение старой не всегда возможно или связано с серьезными издержками. Кроме того, данный подход может усилить автокорреляцию. Эти проблемы ограничивают возможность использования данного метода.
Изменение спецификации модели
В ряде случаев проблема мультиколлинеарности может быть решена изменением спецификации модели: либо изменением формы модели, либо добавлением объясняющих переменных, которые не учтены в первоначальной модели, но существенно влияющие на зависимую переменную.
Использование предварительной информации о некоторых параметрах
Иногда при построении модели множественной регрессии можно воспользоваться некоторой предварительной информацией, в частности, известными значениями некоторых коэффициентов регрессии. Вполне вероятно, что значения коэффициентов, полученные для каких-либо предварительных (обычно более простых) моделей, либо для аналогичной модели по ранее полученной выборке, могут быть использованы для разрабатываемой в данный момент модели.
Для иллюстрации приведем следующий пример. Строится регрессия. Предположим, что переменные X1 и X2 коррелированы. Для ранее построенной модели парной регрессии Y = γ0 + γ1X1+υ был определен статистически значимый коэффициент γ1 (для определенности пусть γ1 = 0.8), связывающий Y с X1. Если есть основания думать, что связь между Y и X1 останется неизменной, то можно положить γ1 = β1 = 0.8. Тогда:
Y = β0 + 0.8X1 + β2X2 + ε. ⇒ Y – 0.8X1 = β0 + β2X2 + ε.
Уравнение фактически является уравнением парной регрессии, для которого проблема мультиколлинеарности не существует.
Ограниченность использования данного метода обусловлена:
получение предварительной информации зачастую затруднительно,
вероятность того, что выделенный коэффициент регрессии будет одним и тем же для различных моделей, не высока.
Преобразование переменных
В ряде случаев минимизировать либо вообще устранить проблему мультиколлинеарности можно с помощью преобразования переменных.
Например, пусть эмпирическое уравнение регрессии имеет вид Y = b0 + b1X1 + b2X2
причем X1 и X2 − коррелированные переменные. В этой ситуации можно попытаться определять регрессионные зависимости относительных величин. Вполне вероятно, что в аналогичных моделях, проблема мультиколлинеарности будет отсутствовать.
Метод главных компонент является одним из основных методов исключения переменных из модели множественной регрессии.
Данный метод используется для исключения или уменьшения мультиколлинеарности факторных переменных модели регрессии. Суть метода: сокращение числа факторных переменных до наиболее существенно влияющих факторов. Это достигается с помощью линейного преобразования всех факторных переменных xi (i=0,…,n) в новые переменные, называемые главными компонентами, т. е. осуществляется переход от матрицы факторных переменных Х к матрице главных компонент F. При этом выдвигается требование, чтобы выделению первой главной компоненты соответствовал максимум общей дисперсии всех факторных переменных xi (i=0,…,n), второй компоненте – максимум оставшейся дисперсии, после того как влияние первой главной компоненты исключается и т. д.
Если ни одну из факторных переменных, включённых в модель множественной регрессии, исключить нельзя, то применяют один из основных смещённых методов оценки коэффициентов модели регрессии – гребневую регрессию или ридж (ridge). При использовании метода гребневой регрессии ко всем диагональным элементам матрицы (ХТХ) добавляется небольшое число τ: 10-6 ‹ τ ‹ 0.1. Оценивание неизвестных параметров модели множественной регрессии осуществляется по формуле:
![]() где
ln – единичная матрица.
где
ln – единичная матрица.
