28. Прогнозирование временных рядов. Показатели точности прогнозов.

29

30

30. Тест Чоу диагностики включения фиктивных переменных в эконометрическую модель.

Тест Чоу — применяемая в эконометрике процедура проверки стабильности параметров регрессионной модели, наличия структурных сдвигов в выборке. Фактически тест проверяет неоднородность выборки в контексте регрессионной модели.

Примером использования данного критерия может служить задача, которую решал Чоу. Он тестировал свой метод на рядах месячных данных о сделках на различные виды продукции: перчатки, смазочные материалы, сальники, подшипники и т.д. Данные представляли собой разнообразные образцы поведения экономических временных рядов, включая циклическое движение. В 59 случаев из 60 предлагаемый метод показал преимущества перед стандартной процедурой и в одном случае результаты были почти одинаковы.

Чтобы проверить следует ли разбивать выборку наблюдений на части и строить для каждой из них свою модель (т.е. привлекать фиктивные переменные), либо ограничиться построением общей модели по всем полученным наблюдениям используют критерий Чоу (об однородности выборки).

Приведем алгоритм его описания для двух специальных случаев:

Случай 1. Пусть объемы подвыборок исравнимы по величине.

Шаг 1. По общей выборке объема оценивают модель по МНК и находят сумму квадратов остатков.

Шаг 2. По подвыборке оценивают модель по МНК и находят соответствующую ей.

Шаг 3. По подвыборке оценивают модель по МНК и находят.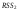

Шаг 4. Рассчитывают решающую функцию критерия:

.

Шаг 5. Если статистика превысит пороговое значение, равное квантилю распределения Фишера на уровне значимостисо степенями свободыи, то необходимо привлекать фиктивные переменные для построения двух моделей.

Случай 2. Если объем , причемсравним по величине с числом параметров модели, тогда алгоритм теста Чоу имеет вид:

Шаг 1. По выборке объема оценивают параметры модели по МНК и вычисляют.

Шаг 2. По общей выборке находят .

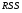Шаг 3. Вычисляют статистику .

Шаг 4. Если >, где– квантиль распределения Фишера на уровне значимостисо степенями свободыи, то следует привлекать фиктивные переменные для описания модели.

31

32. Системы одновременных эконометрических уравнений (соу). Структурная и приведенная форма соу (графическое и матричное представление).

Систему взаимосвязанных тождеств и регрессионных уравнений, в которой переменные могут одновременно выступать как эндогенные (результирующие) в одних уравнениях и как экзогенные (объясняющие) в других, принято называть системой одновременных эконометрических уравнений (СОУ). При этом в уравнения могут входить переменные, относящиеся к предшествующим моментам времени, которые называются лаговыми (запаздывающими). Классический МНК не применим к оцениванию параметров СОУ, поскольку нарушается предположение о независимости экзогенных и шоковых переменных.

Приведем простой пример структурной СОУ, содержащей тождества. А на рис приведено удобное графическое изображение СОУ – причинная диаграмма, в которой экзогенные переменные помещаются в квадратах, а эндогенные – в кругах; взаимосвязи отмечаются стрелками с указанием коэффициентов при объясняющих переменных.

Заметим, что число уравнений и тождеств СОУ должно совпадать с числом эндогенных переменных.

Структурная форма СОУ непосредственно неприменима для решения задач оценивания и прогнозирования, так как уравнения системы не разрешены относительно эндогенных переменных. Поэтому осуществляют преобразование структурной формы СОУ в так называемую приведённую форму, в которой правые части уравнений не содержат эндогенных переменных (т.е. выражаем Y). В общепринятом в литературе виде приведенная форма СОУ записывается:

, где …

Здесь уже справедлива гипотеза о независимости шоковой и экзогенныхпеременных, и для оценивания мультипликаторов можно применить МНК, который носит название косвенного МНК, т.к. строит оценки для π, по которым надо еще пересчитать оценки a и b. Например:.

Однако, оценки, полученные по косвенному МНК, не являются несмещенными, поэтому разработан специальный двухшаговый МНК: 1 шаг) Преобразуем структурную форму СОУ к приведенной, к которой применим классический МНК. 2 шаг) Подставим в исходную структурную форму СОУ оценки эндогенных переменных и, полученные на предыдущем шаге алгоритма. К полученной СЭУ снова применим классический МНК, которые будут обладать свойствами несмещенности и асимптотической состоятельности.

Коэффициенты приведенной формы называют мультипликаторами, которые измеряют эффект воздействия стоящего при них сомножителя-экзогенной переменной на эндогенную, причем различают:

• импульсные – измеряющие эффект воздействия экзогенной переменной на эндогенную в тот же период времени (t);

• автономные - соответствуют свободному члену;

• динамические - соответствуют коэффициенту при лаговой переменной.

Матричное выражение системы одновременных моделей, состоящих из n уравнений с n + m переменными: BY+CX=E; где - вектор предопределенных (экзогенных и лаговых эндогенных) переменных;- вектор эндогенных переменных;- матрица коэффициентов;- матрица коэффициентов; O – нулевой вектор.