- •Белорусский государственный университет
- •Пример выполнения задания (вариант №12)
- •Решение
- •Задание 2 Исследование относительного движения материальной точки
- •Пример выполнения задания (вариант №12)
- •Решение
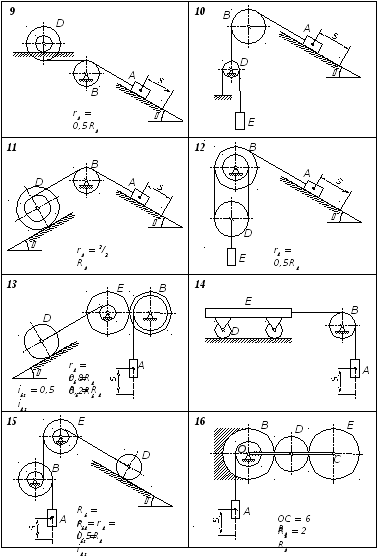
- •Задание 3 Применение теоремы об изменении кинетического момента к определению угловой скорости твердого тела
- •Осевые моменты инерции однородных пластинок
- •Пример выполнения задания (вариант №12)
- •Решение
- •Задание 4 Применение теоремы об изменении кинетической энергии к изучению движения механической системы
- •Пример выполнения задания (вариант №12)
- •Решение
- •Задание 5 Исследование плоского движения твердого тела
- •Пример выполнения задания (вариант №12)
- •Задание 6 Применение уравнений Лагранжа второго рода к исследованию движения механической системы с двумя степенями свободы
- •Пример выполнения задания (вариант №12)
- •Решение
Пример выполнения задания (вариант №12)
Дано:
![]() кг;
кг;![]() кг;
кг;![]() сек–1;
сек–1;![]() м;
м;![]() м;
м;![]() м;
м;![]() Н·м;
Н·м;![]() сек;
сек;![]() сек;
сек;![]() м.
м.
Найти угловую скорость тела
![]() при
при![]() и при
и при![]() .
.
Решение
К решению задачи применим теорему об
изменении кинетического момента
механической системы, выраженную
уравнением:
решению задачи применим теорему об
изменении кинетического момента
механической системы, выраженную
уравнением:
![]() ,
,
где
![]() – кинетический момент системы, состоящей
из тела
– кинетический момент системы, состоящей
из тела![]() и точки
и точки![]() ,
относительно оси
,
относительно оси![]() ;
;![]() – главный момент внешних сил, приложенных
к системе, относительно оси
– главный момент внешних сил, приложенных
к системе, относительно оси![]() .
.
На систему за время от
![]() до
до![]() действуют силы: вес
действуют силы: вес![]() тела, вес
тела, вес![]() точки
точки![]() ,
пара сил с моментом
,
пара сил с моментом![]() и реакции подпятника и подшипника.
и реакции подпятника и подшипника.
Предполагая вращение тела
![]() против часовой стрелки, найдем текущее
значение кинетического момента системы,
который складывается из кинетического
момента тела
против часовой стрелки, найдем текущее
значение кинетического момента системы,
который складывается из кинетического
момента тела![]() и момента количества движения точки
и момента количества движения точки![]() ,
находящейся в точке
,
находящейся в точке![]() тела
тела![]() (в нашем случае точка
(в нашем случае точка![]() совпадает с точкой
совпадает с точкой![]() )
и имеющей скорость
)
и имеющей скорость![]() :
:
![]() .
.
Таким образом,
![]() .
.
Главный момент внешних сил равен
вращающему моменту
![]() ,
так как другие силы момента относительно
оси
,
так как другие силы момента относительно
оси![]() не создают. Уравнение, выражающее теорему
об изменении кинетического момента,
примет вид
не создают. Уравнение, выражающее теорему
об изменении кинетического момента,
примет вид
![]() ,
(1)
,
(1)
где
![]() Н·м,
а
Н·м,
а![]() кг·м2.
кг·м2.
Разделим в уравнении (1) переменные и проинтегрируем левую и правую части уравнения:
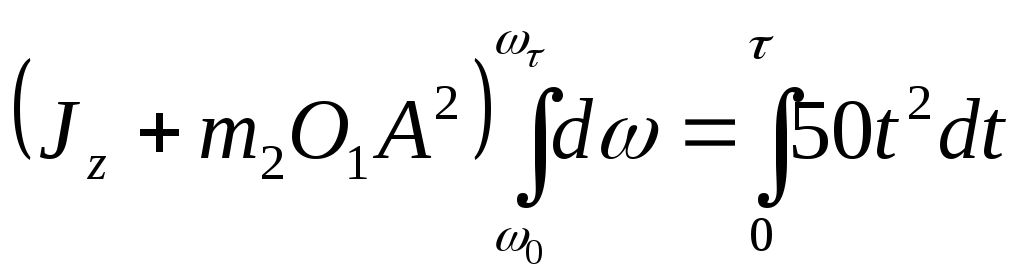 ,
,
откуда
![]() .
(2)
.
(2)
Подставив в уравнение (2) числовые значения уже известных величин, получаем
![]() ,
,
![]() сек–1.
сек–1.
В течение промежутка времени от
![]() до
до![]() на систему действуют силы
на систему действуют силы![]() ,
,![]() ,
реакции подпятника и подшипника.
Поскольку вращающий момент
,
реакции подпятника и подшипника.
Поскольку вращающий момент![]() снимается, т. е.
снимается, т. е.![]() ,
то
,
то
![]()
 ,
,![]() const.
const.
Определим значения кинетических моментов
![]() при
при![]() и
и![]() при
при![]() и приравняем эти значения.
и приравняем эти значения.
Для
![]()
![]() кг·м2/сек.
(3)
кг·м2/сек.
(3)
При
![]() скорость точки
скорость точки![]() складывается из относительной скорости
складывается из относительной скорости![]() по отношению к телу
по отношению к телу![]() и переносной скорости
и переносной скорости![]() в движении вместе с телом
в движении вместе с телом![]() .
Поэтому для
.
Поэтому для![]() покажем два вектора количества движения
точки:
покажем два вектора количества движения
точки:![]() и
и![]() .
В нашем случае линия действия вектора
.
В нашем случае линия действия вектора![]() пересекает ось
пересекает ось![]() ,
следовательно, кинетический момент
вектора
,
следовательно, кинетический момент
вектора![]() относительно этой оси равен нулю.
относительно этой оси равен нулю.
Для
![]() :
:
![]() . (4)
. (4)
Величину отрезка
![]() можно найти из выражения:
можно найти из выражения:
![]()
В момент времени
![]() точка
точка![]() окажется на расстоянии
окажется на расстоянии![]() ,
отсчитываемом вдоль желоба
,
отсчитываемом вдоль желоба![]() ,
от точки
,
от точки![]() .
Это равносильно тому, что
.
Это равносильно тому, что
![]() ,
,![]() ,
,
из чего следует
![]() м.
м.
В результате уравнение кинетического момента (4) примет вид:
![]() .
.
Приравнивая
![]() и
и![]() :
:
![]() ,
,
находим
![]() сек–1.
сек–1.
Ответ:![]() сек–1,
сек–1,![]() сек–1.
сек–1.
Задание 4 Применение теоремы об изменении кинетической энергии к изучению движения механической системы
Механическая система под действием сил
тяжести приходит в движение из состояния
покоя. Учитывая трение скольжения тела
![]() (варианты 1–3, 5, 6, 8–12, 17–23) и сопротивление
качению тела
(варианты 1–3, 5, 6, 8–12, 17–23) и сопротивление
качению тела![]() ,
катящегося без скольжения (варианты 2,
4, 6–9, 11, 13–15, 20, 21, 24), пренебрегая другими
силами сопротивления и массами нитей,
предполагаемых нерастяжимыми, определить
скорость тела
,
катящегося без скольжения (варианты 2,
4, 6–9, 11, 13–15, 20, 21, 24), пренебрегая другими
силами сопротивления и массами нитей,
предполагаемых нерастяжимыми, определить
скорость тела![]() в тот момент, когда пройденный им путь
станет равным
в тот момент, когда пройденный им путь
станет равным![]() .
.
В задании приняты следующие обозначения:
![]() – массы тел
– массы тел![]() ;
;![]() – радиусы больших и малых окружностей;
– радиусы больших и малых окружностей;![]() – радиусы инерции тел
– радиусы инерции тел![]() и
и![]() относительно горизонтальных осей,
проходящих через их центры тяжести;
относительно горизонтальных осей,
проходящих через их центры тяжести;![]() – углы наклона плоскостей к горизонту;
– углы наклона плоскостей к горизонту;![]() – коэффициент трения скольжения тела
– коэффициент трения скольжения тела![]() ;
;![]() – коэффициент трения качения тела
– коэффициент трения качения тела![]() .
.
Необходимые для решения данные приведены
в табл. 4. Блоки и катки, для которых
радиусы инерции в таблице не указаны,
считать сплошными однородными цилиндрами.
Во всех вариантах
![]() .
.
Таблица 4
|
№ |
|
|
|
|
|
|
|
|
|
f |
см |
м |
Дополнительные данные |
|
кг |
см |
см |
град | ||||||||||
|
1 |
4m |
m/5 |
4m/3 |
– |
– |
– |
– |
60 |
– |
0,10 |
– |
2 |
|
|
2 |
m/2 |
m/3 |
– |
– |
30 |
– |
20 |
30 |
45 |
0,22 |
0,20 |
2 |
|
|
3 |
m |
m/10 |
m |
– |
– |
– |
– |
45 |
– |
0,10 |
– |
2 |
|
|
4 |
2m |
40m |
m |
20 |
40 |
18 |
– |
– |
– |
– |
0,30 |
|
массами FK, KC и ползуна K пренебречь |
|
5 |
2m |
m |
– |
20 |
15 |
18 |
– |
60 |
– |
0,12 |
– |
|
массой водила пренебречь |
|
6 |
3m |
m |
– |
– |
28 |
– |
– |
30 |
45 |
0,10 |
0,28 |
1,5 |
|
|
7 |
2m |
2m |
– |
16 |
25 |
14 |
– |
30 |
– |
– |
0,20 |
2 |
|
|
8 |
m/2 |
m/3 |
– |
– |
30 |
– |
– |
30 |
45 |
0,15 |
0,20 |
1,75 |
|
|
9 |
2m |
9m |
– |
– |
30 |
– |
20 |
30 |
– |
0,12 |
0,25 |
1,5 |
|
|
10 |
m/4 |
m/4 |
m/5 |
– |
– |
– |
– |
60 |
– |
0,10 |
– |
3 |
|
|
11 |
m/2 |
m/4 |
– |
– |
30 |
– |
25 |
30 |
45 |
0,17 |
0,20 |
2,5 |
|
|
12 |
m/2 |
m/5 |
m |
30 |
– |
20 |
– |
30 |
– |
0,20 |
– |
2,5 |
|
|
13 |
2m |
5m |
2m |
30 |
20 |
26 |
– |
30 |
– |
– |
0,24 |
2 |
|
|
14 |
m/2 |
5m |
4m |
– |
25 |
– |
– |
– |
– |
– |
0,20 |
2 |
массы колес равны |
|
15 |
m/2 |
4m |
m/2 |
20 |
15 |
18 |
– |
60 |
– |
– |
0,25 |
1,5 |
|
|
16 |
m/10 |
m/20 |
m/10 |
10 |
12 |
– |
– |
– |
– |
– |
– |
|
массой водила пренебречь |
|
17 |
m/4 |
m/5 |
m/10 |
20 |
– |
15 |
– |
60 |
– |
0,10 |
– |
|
шатун EF – тонкий однородный стержень |
|
18 |
3m |
m |
– |
35 |
15 |
32 |
– |
60 |
– |
0,15 |
– |
|
массой водила пренебречь |
|
19 |
m/3 |
m/10 |
m |
24 |
– |
20 |
– |
60 |
– |
0,15 |
– |
1,5 |
|
|
20 |
2m |
20m |
– |
20 |
15 |
16 |
– |
30 |
– |
0,10 |
0,20 |
|
массами FK, KC и ползуна K пренебречь |
|
21 |
m |
2m |
– |
20 |
20 |
16 |
– |
30 |
45 |
0,20 |
0,32 |
1,2 |
|
|
22 |
m/2 |
m/4 |
– |
20 |
10 |
– |
– |
60 |
– |
0,17 |
– |
|
массой водила пренебречь |
|
23 |
m |
m/10 |
4m/5 |
20 |
– |
18 |
– |
30 |
– |
0,10 |
– |
1 |
|
|
24 |
3m |
20m |
– |
20 |
30 |
18 |
– |
– |
– |
– |
0,60 |
|
массами FK, KC и ползуна K пренебречь |