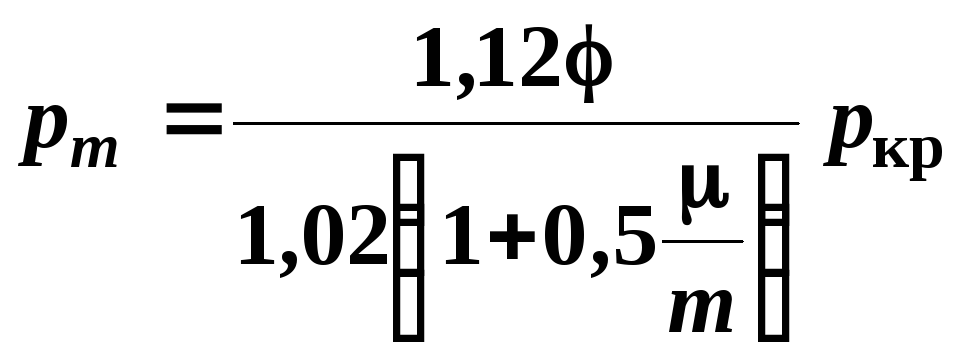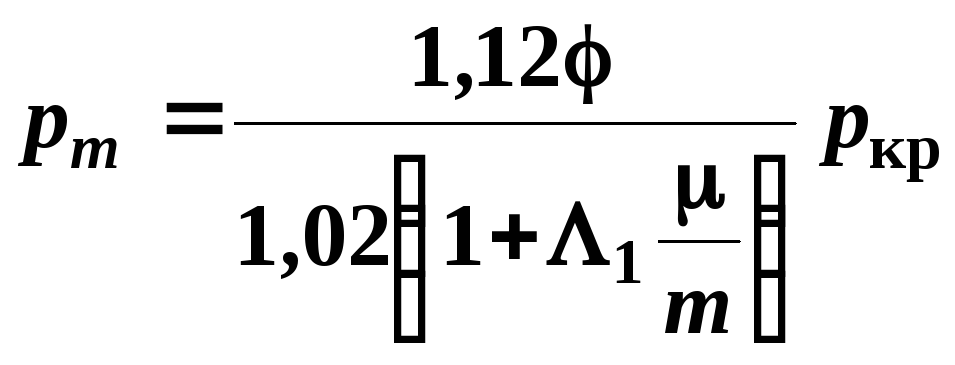147

6. Пример расчета ствола-моноблока

Пусть необходимо разработать эскизный проект ствола-моноблока артиллерийского орудия для следующих исходных данных:

калибр орудия мм;

масса снаряда кг;

дульная скорость снаряда м/с.

6.1. Баллистическое проектирование ствола-моноблока

Задаемся характеристиками пороха (в соответствии с таблицами внутренней баллистики):

сила пороха ;

коволюм ;

плотность пороха ;

коэффициенты формы порохового зерна ;.

Также принимаем:

параметр расширения пороховых газов ;

давление форсирования .

По формулам (4.2) и (1.3) вычисляем коэффициент могущества проектируемого орудия и коэффициент массы снаряда:

;

.

Так как коэффициент , то для определения исходного варианта условий заряжания проведем уточнение коэффициента могущества орудия.

По табл. 4.1 методом линейного интерполирования определяем коэффициент использования метательного заряда , соответствующий полученному значению:

,	,
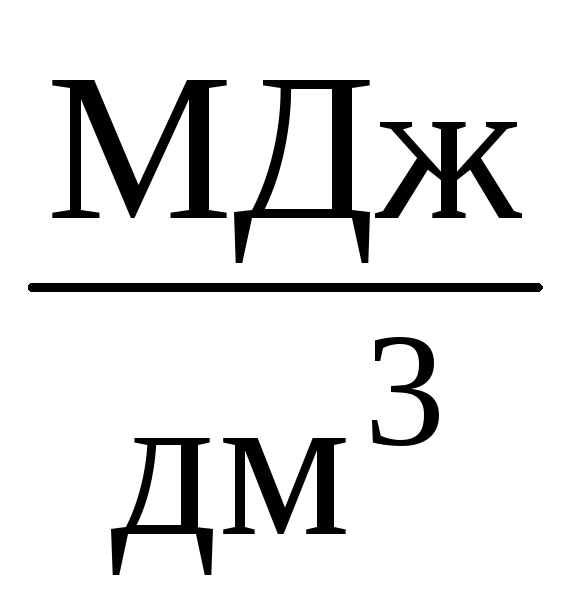
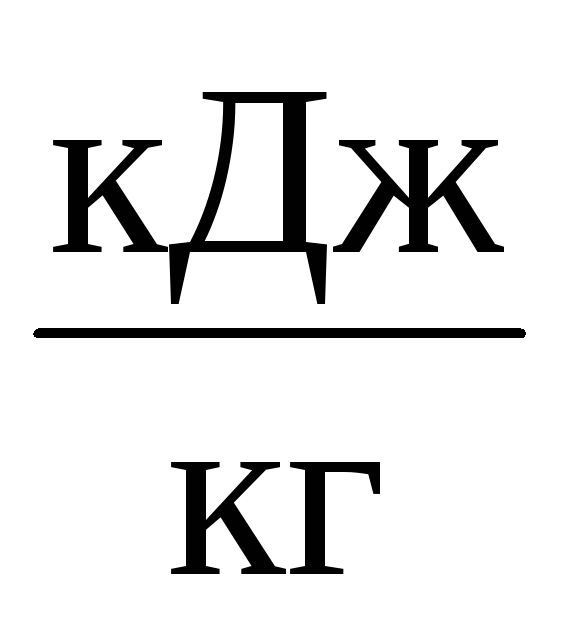
2	1 274
2,801	1 248,4
3	1 242

Таким образом, .

Для полученного значения по формуле (4.5) рассчитываем массу заряда:

.

По формуле (4.6) определяем массу снаряда, у которого коэффициент массы кг/дм³:

.

По формулам (4.7) рассчитываем коэффициенты фиктивности (для заданного снаряда) и(для снаряда, у которого коэффициент массыкг/дм³), полагая массу заряда одинаковой для обоих снарядов и принимая (т.е. уширение каморы пока не учитываем):

;

,

где значение коэффициента принимаем в соответствии с рекомендациями (4.8).

По формуле (4.4) определяем дульную скорость, которую имел бы снаряд с коэффициентом массы кгс/дм³:

м/с.

По полученным значениям ивычисляем коэффициент могущества:

.

Полученное значение и является входным параметром в табл. 1.1.

По табл. 4.1, используя метод линейного интерполирования, определяем исходный вариант условий заряжания орудия. Результаты вычислений заносим в табл. 6.1.

Таблица 6.1

Определение исходного варианта условий заряжания

, МДж/дм3	, МПа	, кгс/дм3	, кДж/кг			, м/с
2	192	0,58	1 274	1,09	29	573
2,831	212,775	0,630	1 247,408	1,173	38,141	617,874
3	217	0,64	1 242	1,19	40	627

Для дальнейших расчетов используем значения:

крешерного давления МПа;

плотности заряжания кг/дм³;

коэффициента использования метательного заряда кДж/кг;

коэффициента уширения каморы .

Значения остальных параметров являются ориентировочными:

длина ствола в калибрах ;

дульная скорость снаряда м/с.

Для полученного значения по формуле (4.5) вычисляем массу метательного заряда:

кг.

По формуле (1.1) рассчитываем площадь поперечного сечения канала ствола:

,

где значение коэффициента принимаем в соответствии с рекомендациями (1.2).

Проводим расчет отдельных вариантов для полученной массы метательного заряда и измененной на 10 % по схеме, приведенной в табл. 4.3. Результаты вычислений заносим в табл. 6.2.

Таблица 6.2

Баллистический расчет ствола

№ п/п	Формула	Размерность	Результат вычислений
			1	2	3
1		кг	3,670	4,078	4,486
2		дм3	5,825	6,473	7,121
3		дм	4,830	5,367	5,905
4		–	1,116	1,122	1,128

Окончание табл. 6.2

№ п/п	Формула	Размерность	Результат вычислений
			1	2	3
5		МПа	240,663	239,904	239,157
6			2 454,76	2 447,02	2 439,40
7		м/c	1 759	1 673	1 599
8	(из ТБР по ,, и)	–	8,282	6,519	5,395
9	(из ТБР по и)	–	2,975	2,998	3,022
10		–	0,36	0,46	0,56
11		дм	40,00	34,99	31,86
12		дм	4,118	4,575	5,034
13		–	37,66	33,93	31,74
14		–	2,154	2,512	2,622

Для перевода значений давлений в кгс/см² (строка 6 табл. 6.2) используем соотношение .

Для определения (строка 8 табл. 6.2) проводим двойное интерполирование: сначала по величине давления, а затем – по табличному значению дульной скорости. Для определения(строка 9 табл. 6.2) проводим линейное интерполирование по величине давления.

Получим:

при кг:

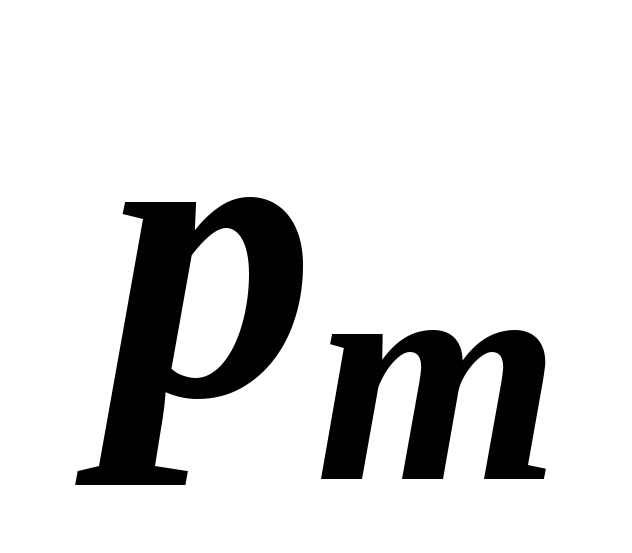
	2 400	2 454,76	2 600
8,0	1 738	1 748	1 773
8,282		1 759
9,0	1 778	1 787	1 811
…
	3,142	2,975	2,531

при кг:

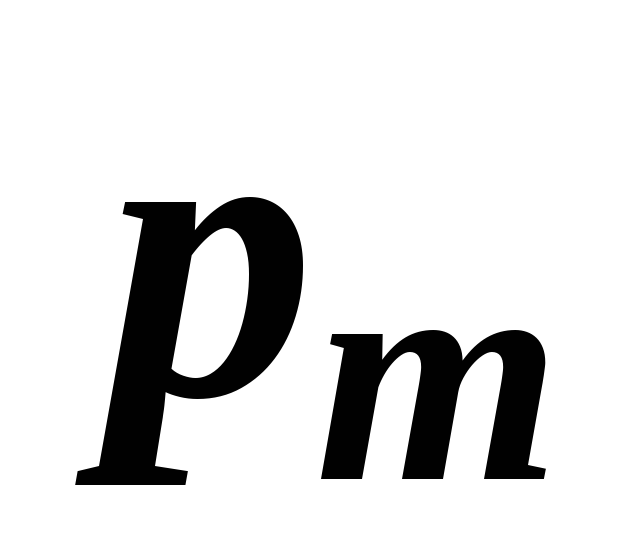
	2 400	2 447,02	2 600
6,5	1 663	1 672	1 702
6,519		1673
7,0	1 690	1 699	1 728
…
	3,142	2,998	2,531

при кг:

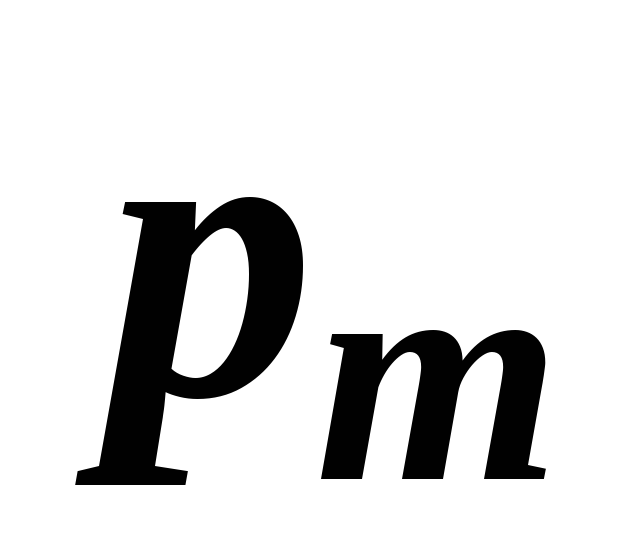
	2 400	2 439,40	2 600
5,0	1 561	1 569	1 603
5,395		1 599
5,5	1 599	1 607	1 640
…
	3,142	3,022	2,531

При вычислении критерия (строка 14 табл. 6.2) принято.

Исходя из наибольшего значения критерия , для дальнейших расчетов выбираем третий вариант условий заряжания артиллерийского орудия.

Уточнение выбранного варианта условий заряжания производим по схеме, приведенной в табл. 4.4 (при этом уточняем длину ствола с учетом влияния уширения каморы и запаса дульной скорости порядка ). Результаты вычислений заносим в табл. 6.3.

Таблица 6.3

Уточнение выбранного варианта

№ п/п	Формула	Размерность	Результат вычислений
1		–	0,488
2		–	0,325
3		–	1,126
4		МПа	239,265
5			2 440,50
6		м/с	1 614
7	(из ТБР по ,, и)	–	5,603
8		дм	33,086
9		–	32,75
10	(из ТБР по и)	–	2,069
11			1 214

Для определения (строка 7 табл. 6.3) проводим двойное интерполирование: сначала по величине давления, а затем по табличному значению дульной скорости. Для определения параметра(строка 10 табл. 6.3) проводим линейное интерполирование по величине давления.

Получим:

	2 400	2 440,50	2 600
5,5	1 599	1 607	1 640
5,603		1 614
6,0	1 633	1 641	1 673
…
	2,106	2,069	1,924

По полученному значению конечного импульса давления пороховых газов в соответствии с табл. 4.5 выбираем марку пороха: семиканальный пироксилиновый порох марки 12/7 для полного заряда.

Таким образом, получены следующие условия заряжания проектируемого артиллерийского орудия:

масса снаряда кг;

масса метательного заряда кг;

объем зарядной каморы дм³;

плотность заряжания кг/дм³;

коэффициент уширения зарядной каморы ;

приведенная длина зарядной каморы дм;

длина каморы дм;

параметр заряжания Н. Ф. Дроздова ;

дульный путь снаряда дм;

дульный относительный путь снаряда ;

коэффициент фиктивности .

Для полученных условий заряжания с помощью таблиц внутренней баллистики решаем прямую задачу внутренней баллистики.

Для этого по значениям ииз таблиц внутренней баллистики методом линейного интерполирования определяем табличные значения(кгс/см²),,, которые вносим в табл. 6.4 (столбцы 3, 5, 7 соответственно).

Таблица 6.4

Результаты решения прямой задачи внутренней баллистики

	,	,	,	,	,	,	,
	дм	кгс/см2	МПа	м/с	м/с	с/дм	мс
1	2	3	4	5	6	7	8
0	0	300	29,42	0	0	0	0
0,2	1,181	1 946	190,84	294	125,2	202	2,8
0,4	2,362	2 342	229,67	472	201,1	255	3,5
	3,720	2 429	238,20	628	267,5	297	4,1
1,0	5,905	2 301	225,65	817	348,0	347	4,8
2,0	11,810	1 789	175,44	1 141	486,1	448	6,2
	17,987	1 414	138,66	1 349	574,7	531	7,4
4,0	23,620	1 049	102,87	1 476	628,8	598	8,3
5,0	29,525	820	80,41	1 569	668,4	664	9,2
	33,086	722	70,80	1 614	687,6	701	9,7

Путь снаряда по каналу ствола (столбец 2 табл. 6.4) определяем по формуле .

Для определения табличных значений пиродинамических элементов в момент вылета снаряда из канала ствола проводим двойное интерполирование: сначала по параметру, а затем – по относительному пути снаряда:

Давления

	2,0	2,069	2,1
5,5	731	736	738
5,603		722
6,0	663	668	670

Скорости

	2,0	2,069	2,1
5,5	1 623	1 607	1 600
5,603		1 614
6,0	1 656	1 641	1 634

Времена

	2,0	2,069	2,1
5,5	687	695	699
5,603		701
6,0	718	726	730

Перевод давлений в паскали (столбец 4 табл. 6.4) осуществляем, используя соотношение

.

Действительные значения скоростей и времен (столбцы 6 и 8 табл. 6.4) вычисляем по формулам:

;

.

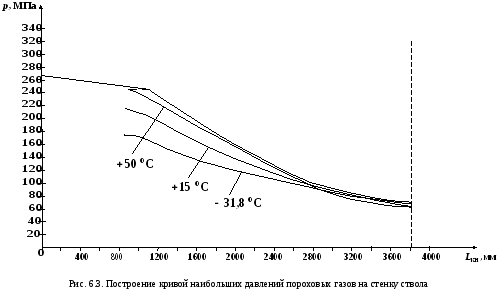
На основе полученных данных строим пиродинамические кривые (рис. 6.1 и 6.2).

Для построения кривой наибольших давлений необходимо рассчитать давления пороховых газов для предельных температур, задаваемых в ТТЗ (обычно 50^оС).

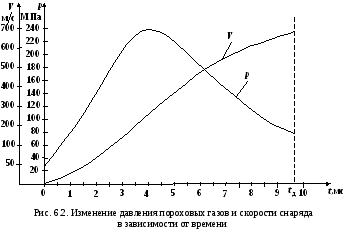
По табл. 4.6 методом линейного интерполирования определяем значение коэффициента для максимального давления пороховых газовМПа при температуре метательного заряда^оС и плотности заряжания:

Значения

, МПа	, кг/дм3
	0,6	0,63	0,7
220	0,36	0,36	0,36
238,2		0,369
240	0,37	0,37	0,37

Таким образом, .

Отклонения максимального давления для предельных температур рассчитываем по поправочной формуле (4.9). Получим:

МПа;

МПа.

Максимальное давление пороховых газов при предельных температурах метательного заряда определяем по формуле (4.10). Получим:

МПа;

МПа.

Проверим выполнение условия . Для этого из таблиц внутренней баллистики (ч.I) по значениямМПаикг/дм³находим:

Давления

	7,593	7,758	8,641
	1 856	1 847	1 799

Таким образом, .

Так как условие не выполняется, то необходимо вычислить температуру заряда, при которой.

Для этого по значениям кг/дм³ииз таблиц внутренней баллистики (ч. I) определяем:

Давления

	5,161	5,603	5,867
	2 054	2 010	1 983

Таким образом, .

Вычисляем приращение максимального давления:

МПа.

Тогда отклонение температуры заряда от +15 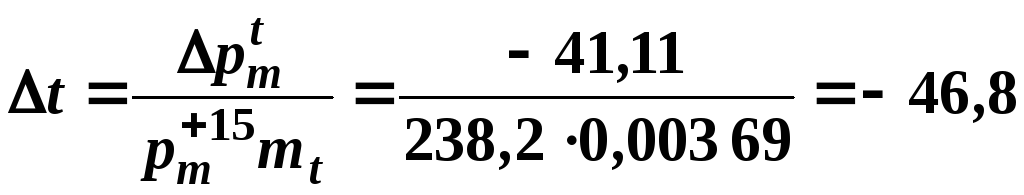^оС:

^оС,

а температура заряда, при которой :

^оС.

Для предельных температур заряда +50 ^оС и –31,8 ^оС по значениям максимальных давлений МПа (2 744 кгc/см²) и МПа (2 010 кгc/см²) при плотности заряжания кг/дм³ из таблиц внутренней баллистики (ч. I) находим значения параметра Н. Ф. Дроздова и. Получим:

при ^оС:

Давления

	1,8	1,807	1,9
	2 754	2 744	2 619

при ^оС:

Давления

	2,5	2,562	2,6
	2 054	2 010	1 983

Таким образом, ,.

По полученным значениям параметра Н. Ф. Дроздова при заданной плотности заряжания из таблиц внутренней баллистики (ч. I), начиная от максимального баллистического давления пороховых газов, по направлению к дульному срезу определяем баллистические давления и переводим их в паскали. Результаты вычислений заносим в табл. 6.5 (столбцы 6, 7 и 9, 10). В эту же таблицу (столбцы 3 и 4) из табл. 6.4 переписываем значения баллистических давлений для температуры метательного заряда +15 ^оС.

Таблица 6.5

Данные для построения кривой наибольших давлений пороховых газов на стенку ствола

	,	,	,	,	,	,	,	,	,	,
	дм	кгc/см2	МПа	МПа	кгc/см2	МПа	МПа	кгc/см2	МПа	МПа
1	2	3	4	5	6	7	8	9	10	11
0,602	3,555	–	–	–	–	–	–	2 010	197,11	175,58
0,63	3,720	2 429	238,20	215,81	–	–	–	–	–	–
0,638	3,779	–	–	–	2 745	269,19	243,89	–	–	–
1,0	5,905	2 301	225,65	204,44	2 609	255,85	231,80	1 890	185,34	167,92
2,0	11,810	1 789	175,44	158,95	2 025	198,58	179,91	1 476	144,74	131,13
2,207	13,032	–	–	–	1 938	190,05	172,19	–	–	–
3,046	17,987	1 414	138,66	125,63	–	–	–	–	–	–
4,0	23,620	1 049	102,87	93,20	1 020	100,03	90,63	967	94,83	85,92
5,0	29,525	820	80,41	72,85	798	78,26	70,90	827	81,10	73,48
5,603	33,086	722	70,80	64,14	703	68,94	62,46	766	75,12	68,06

Для определения значения давления в момент вылета снаряда из канала ствола при температуре метательного заряда +50^оС проводим двойное интерполирование: сначала по параметру, а затем – по относительному пути снаряда:

Давления

	1,8	1,807	1,9
5,5	717	717,49	724
5,603		703
6,0	649	649,49	656

При температуре метательного заряда –31,8 ^оС баллистическое давление пороховых газов в момент вылета снаряда из канала ствола определяется как для момента окончания горения порохового заряда, то есть.

По формуле (4.11) рассчитываем соответствующие давления на дно снаряда:

,

где – коэффициент, учитывающий влияние нарезов на движение снаряда.

Результаты расчетов вносим в табл. 6.5 (столбцы 5, 8, 11).

По формуле (4.12) рассчитываем максимальное давление пороховых газов на дно канала ствола при температуре метательного заряда +50 ^оС:

МПа.

При построении кривой наибольших давлений пороховых газов на стенку ствола (рис. 6.3) расчетное положение точки смещаем к дульному срезу на 2 калибра. Полученную точку соединяем прямой линией с точкой, соответствующей значению. От смещенной точкипо направлению к дульному срезу проводим огибающую кривых давлений сначала к точке, соответствующей концу горения заряда при температуре +50^оС, а дальше – касаясь наибольших давлений.