24 Ошибки при обработке управляющего воздействия.

Обычно точность следящей системы при управлении оценивают по точности воспроизведения входного сигнала, меняющегося с постоянной скоростью, с постоянным ускорением или по гармоническому закону. Обычно, исходя из требований к конкретной следящей системе проектировщику задаются необходимые значения добротности системы по скорости и ускорению ихарактеризующие соответственно ошибки при отработке линейно изменяющегося входного сигнала в системе с астатизмом первого порядка и сигнала, меняющегося с постоянным ускорением системе с астатизмом второго порядка.

Если порядок астатизма равен единице, то передаточная функция разомкнутой системы может быть записана в общем виде так:

.

Добротность по скорости представляет собой величину: .

Заданному значению будет удовлетворять система, низкочастотная асимптота ЛАЧХ которой, имеет наклон – 20дБ/дек, пересекается с осью абсцисс при частоте, равной.

В системе с астатизмом второго порядка, где:

.

Добротность по ускорению:

Низкочастотная асимптота соответствующей ЛАЧХ имеет наклон –40 дБ/дек и пересекает ось абсцисс при частоте равной .

Ошибка системы при обработке гармонического сигнала в нелинейной следящей системе также определяется на основании ЛАЧХ разомкнутой системы. Поскольку амплитудная частотная характеристика при каждой данной частоте представляет собой отношение амплитуд гармонических сигналов на выходе и входе системы, можно записать:

,

где - амплитуда ошибки, так же меняющейся по гармоническому закону с частотой.

Следящая система строится так, чтобы частота среза её ЛАЧХ значительно превышала максимальную частоту гармонического входного сигнала, так как только в этом случае она будет удовлетворительно отрабатывать его. Это дает основание пренебречь единицей по сравнению со значение амплитуды .

Тогда справедливо примерное равенство:

,

т.е. чем меньше должна быть ошибка при данном входном воздействии, тем больше должна быть амплитуда частотной характеристики разомкнутой системы при частоте . Сказанное позволяет построить желаемую ЛАЧХ системы так, чтобы удовлетворялись заданные требования по точности отработки управляющего воздействия.

Повышение точности обработки управляющего воздействия за счет применения комбинированного управления

Возможности повышения точности следящей системы за счет увеличения добротности или порядка астатизма ограничены. Увеличение добротности, т.е. при данном виде передаточной функции, частота среза ЛАЧХ разомкнутой системы, ограничено влиянием малых постоянных времени. Кроме того, при увеличении уменьшается диапазон входных сигналов, при которых система работает как линейная, и растёт влияние помех. Повышение порядка астатизма при данной частоте среза позволяет повысить точность отработки низкочастотных гармонических управляющих воздействий. Однако повышение порядка астатизма ведет к уменьшению запаса устойчивости системы . Эффективным средством повышения точности следящей системы является применение комбинированного управления, при котором в систему наряду с заданием перемещения вводится одна или несколько производных от него. Пусть часть системы, на вход которой через компенсирующий канал с передаточной функцией(Р) вводится компенсирующий сигнал, имеет передаточную функцию(Р), а передаточная функция(Р) определяется как, гдеW(P)-передаточная функция разомкнутой системы (рисунок 6.6).

Рисунок 6.6 – Структурная схема системы с комбинированным управлением

На основании выражения:

,

и с учетом того, что , передаточная функция по управлению для замкнутой системы с компенсирующим каналом может быть записана в виде:

. (6.8)

Вводя понятие эквивалентной передаточной функции как передаточной функции разомкнутой системы, в которой аналогичный переходной процесс по управлению получился бы без введения компенсирующего канала, можно записать:

,

откуда с учетом (6.8):

. (6.9)

Ошибка комбинированной системы оценивается на основании передаточной функции:

. (6.10)

Это выражение позволяет записать условие тождественного равенства нулю ошибки при управлении, то есть условие инвариантности системы о отношению к управлению:

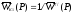. (6.11)

Фактически, вследствие того, что замкнутый контур скорости представляет собой не апериодическое звено, а сложную динамическую систему, полная инвариантность не достигается. Оценим результат применения компенсационного канала с передаточной функцией:

, (6.12)

в реальной системе, с передаточной функцией замкнутого контура скорости . Передаточные функции эквивалентной разомкнутой системы и ошибки могут быть получены путем подстановки в формулы (6.9) и (6.10) значений;и:

;.

Пусть контуры скорости и положения имеют стандартную настройку на оптимум по модулю. Если постоянная времени фильтра тахогенератора Т_дс=0, то коэффициенты регуляторов скорости и положения должны быть выбраны в соответствии с выражениями:

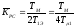;. (6.13)

Cдостаточной степенью точности замкнутый токовый контур можно описать передаточной функцией:

. (6.14)

Тогда передаточная функция разомкнутого контура скорости будет:

, (6.15)

а замкнутого:

. (6.16)

После подстановки выражений для ,ив формулы дляиполучаем:

;

.

Повышение быстродействия по управлению за счет комбинированного управления при неполной инвариантности сопровождается увеличением колебательности. Так, в рассматриваемом случае, перерегулирование при отработке ступенчатого управляющего воздействия (кривая 1, рисунок 6.8) составляет около 55%, в то время как при отсутствии компенсирующего сигнала переходной процесс соответствует настройке на ОМ (кривая 3) и перерегулирование составляет около 4%. Введение компенсационного канала значительно повысило точность отработки системой гармонического входного сигнала.Если, например, входной сигнал имеет частоту , то ошибка уменьшается в 50 раз (точкиина рисунке 6.7).

Реализация двух производных от входного сигнала без замедления представляет технические трудности. Учитывая это целесообразно оценить эффект, который может быть получен в рассматриваемой системе в результате введения только одной производной от входного сигнала при . После подстановки этого выражения в 6.10, а также значенийиприошибка получается в виде:

.

Введение одной производной позволяет исключить скоростную составляющую ошибки, обеспечив свойства системы с астатизмом второго порядка по управлению. На основании 6.9 при передаточная функция эквивалентной разомкнутой системы может быть получена в виде:

.

Соответствующая ЛАЧХ 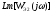приведена на рисунке 6.7 (кривая 2), а реакция системы на скачок управления на рисунке 6.8 (кривая 2).

Рисунок 6.7 – ЛАЧХ эквивалентной разомкнутой системы

Рисунок 6.8 – Реакция системы на скачек управления

Двухканальные следящие привода

Одним из способов повышения точности отработки управляющего воздействия является применение так называемых двухканальных позиционных приводов. Работа таких приводов поясняется следующей структурной схемой (рисунок 6.9):

Рисунок 6.9 – Структурная схема двухканального следящего электропривода

На два канала, передаточные функции которых в разомкнутом состоянии обозначены (Р) и(Р), подаются два управляющих воздействияи. Канал с передаточной функцией(Р) замкнут по собственной выходной координате. Канал с передаточной функцией(Р) замкнут по выходной координате системы, являющейся суммой координати. Управляющее воздействиеявляется основным и должно точно отрабатываться.

_{Воздейс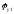твие может вырабатываться программными устройствами и является приближенным (прогнозированным) значением заданного перемещения. При этом первый канал осуществляет грубое, а второй – точное управление перемещением. Часто для обоих используют общее управляющее воздействие. Оценим для этого случая возможности двухканального привода, предполагая, что оба канала обладают статизмом первого порядка и настроены на ОМ. Заменяя в первом приближении реальные передаточные функции упрощенными, можно записать:}

_{; .}

_{Передаточная функция замкнутой системы имеет вид:}

_,

_{А эквивалентной разомкнутой: .}

_{После подстановки сюда выражений для W1(p) и W2(p) получается:}

_(6.17)

_{Очевидно, что реальный вид переходного процесса по управлению зависит от соотношения малых постоянных времени в первом и втором каналах T1m и T1m. Из рисунка 6.10 видно, что величина f1 воспроизводит управляющее воздействие с точностью, определяемой передаточной функцией W1(p), т.е малой постоянной времени Т1m. На входе звена с передаточной функцией W2(p) действует сигнал df2=fу-f1-f2=df1-f2. Следовательно, если бы второй канал обладал абсолютным быстродействием и ошибка df2 равнялось нулю, то выходная величина звена W2(p) равнялась бы ошибке первого канала и истинное значение выходной координаты f=f1+f2 точно равнялось бы предписанному fу. Поскольку создание безинерционного силового канала невозможно, то ошибка воспроизведения будет существовать. На рисунке 6.10 показана реакция системы на управляющее воздействие при Т1m =Т2m =Тm.}

Рисунок 6.10 – Графики реакции системы на управляющее воздействие

Выходная величина первого канала меняется по кривой, соответствующей настройке на ОМ; величина f близка к величине, соответствующей настройке на СО.

_{В общем виде передаточную функцию эквивалентной разомкнутой системы (6.17) можно представить в виде : , гдеDэ –добротность;}

_{nэ – порядок астатизма системы; Wэо(р) – передаточная функция, полиномы числителя и знаменателя которые не имеют нулевых корней, т.е .}

_{Если D1 и D2 – добротности первого и второго каналов , а n1 и n2 - их порядок астатизма, то nэ=n2+n1; Dэ=D1D2, т.е в двух канальном приводе с общим управляющим воздействием порядки астатизма каналов складываются, а их добротности перемножаются.}

_{Одним из исполнений двухканального электропривода (рисунок 6.11) является вариант с электродвигателями М1 и М2 и механическим дифференциалом (МД), угол поворота выходного вала которого f’ является суммой углов поворота f’1 и f’2 (штрихами обозначены величины на приведенные к двигателю). Каждый двигатель питается от своего преобразователя (Пр1 и Пр2) и имеет собственную систему управления замкнутую по f’1 и f’2.}

_{Предполагается, что i1 и i2 включают в себя передаточные числа редукторов Рд1 и Рд2 и передаточные числа дифференциала, благодаря чему можно считать, что коэффициент передачи от каждого входа дифференциала до его выхода равен единице.}

_{Из структурной схемы силовой части (рисунок 6.12) очевидно, что момент сопротивлений Мс распределяется между каналами обратно пропорционально передаточным числам редукторов. Суммарный момент инерции каждого привода включает в себя момент инерции исполнительного органа Jи.о ,приведенный через квадрат соответствующего передаточного числа. Приводы в общем случае нельзя считать независимыми друг от друга из-за наличия перекрестных связей с передаточной функцией и . Взаимовлияние приводов тем меньше ,чем меньше момент инерцииJ’и.о, и тем больше передаточные числа редукторов. Если взаимовлияние пренебрежимо мало, то после замыкание обратных связей по f’1 и f’2 , структурная схема будет соответствовать схеме рисунок 6.11. Взаимовлияние каналов должно быть исследовано в соответствии с полной структурной схемой (рисунок 6.12).}

_{Таким образом, в двух канальных следящих электроприводах можно разделить требуемую добротность между отдельными каналами, причем добротности каждого канала будут невелики и их реализация не встретит технических трудностей. Зона линейности каждого канала может быть расширена за счет уменьшения его коэффициента усиления. Система в целом будет иметь высокую добротность. Двух канальный следящий привод обладает высокой точностью воспроизведения управляющего сигнала, изменяющегося в определенном диапазоне низких частот.}

Рисунок 6.11 – Функциональная схема двухканального электропривода

Рисунок 6.12 – Структурная схема силовой части двухканального электропривода