
metod_tau_kontr_rab
.pdf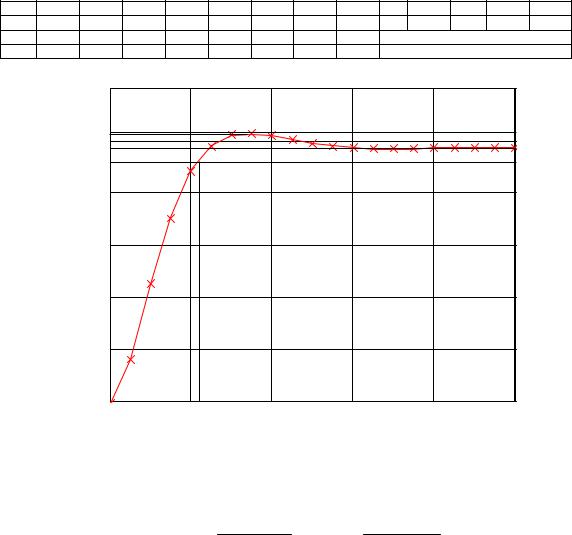
t |
0 |
0.025 |
Таблица 2 – Расчетные данные (переходная характеристика) |
||||||||||
0.05 |
0.075 |
0.1 |
0.125 |
0.15 |
0.175 0.2 0.225 0.25 0.275 0.3 |
||||||||
y(t) 0 |
0.79 |
2.23 |
3.51 |
4.4 |
4.9 |
5.1 |
5.08 |
5 |
4.93 |
4.88 4.85 |
4.844 |
||
t |
0.325 0.35 |
0.375 |
0.4 |
0.425 |
0.45 |
0.475 |
0.5 |
|
|
- |
|
||
y(t) 4.841 4.843 |
4.847 |
4.85 |
4.85 |
4.85 |
4.85 |
4.85 |
|
|
- |
|
|||
|
По рассчитанным данным строится график (рисунок 7) |
|
|
||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
yMAX |
|
|
|
|
|
|
|
|
|
|
|
|
|
yуст 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0.1tрег |
0.2 |
|
0.3 |
|
0.4 |
0.5 |
|
|
Рисунок 7 – Переходная характеристика. |
|
|
8. Показатели качества. |
|
|
Время регулирования – 0,11 сек. |
|
|
Перерегулирование – σ% = yMAX - yуст × 100% = |
5.1 - 4.85 |
× 100% = 5.2% . |
yуст |
4.85 |
|
Литература.
1. Теория автоматического управления. Методические указания. Могилев, 2002
г.
2.Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. –М.: Наука, 1972
3.Руководство к практическому применению преобразования Лапласа и Z- преобразования. –М.: Наука, 1971
Контрольная работа № 1.
Определение передаточных функций. Анализ устойчивости
икачеств системы автоматического регулирования (САР):
1)определить передаточные функции звеньев САР по передаточным функциям, приведённым в таблице 1, путём исключения тех параметров, которые имеют нулевые значения в соответствующем столбце таблицы 2. Номер столбца (см. табл.2) выбирается по предпоследней цифре шифра студента.
По последней цифре шифра выбрать номер рисунка структурной схемы системы (1-10) и зарисовать её с учётом передаточных функций, полученных в пункте 1;
2)произвести необходимые структурные преобразования
изаписать передаточные функции замкнутой САР по задающе-
му |
воздействию Ф(p), по |
возмущающему воздействию Фf(p), |
|||||||||
по |
ошибке от задающего воздействия ΦX(p), по ошибке от |
||||||||||
возмущающего воздействия: |
|
|
|
|
|
|
|
|
|||
|
|
Y ( p) |
Y ( p) |
|
X ( p) |
|
X ( p) |
||||
|
Ф ( p) = |
|
; Фf ( p) = |
|
; |
ФX ( p) = |
|
; |
ФXf ( p) = |
|
|
|
G ( p) |
F ( p) |
G ( p) |
F ( p) |
|||||||
3) оценить устойчивость системы, пользуясь критериями Гурвица и Михайлова. Если система окажется неустойчивой, то изменить коэффициент К5 так, чтобы система стала устойчивой;
4) определить суммарную статическую ошибку системы от задающего и возмущающего воздействия, если принять, что
X(t)=1(t) и F(t)=1(t);
5)определить корни характеристического уравнения САР, нанести их на комплексную плоскость и определить степень устойчивости САР (см. приложение 1).
6)по передаточной функции замкнутой системы по задающему воздействию, используя таблицу преобразований Лапласа или теорему разложения, получить выражение для переходной характеристики САР y(t) - при действии на входе единичного ступенчатого сигнала x(t)=1(t) (см. приложение
2);
7)построить полученную переходную характеристику в таком диапазоне времени t, когда её величина y(t) не будет отличаться от у(∞) более, чем на 2-5%, где у(∞) - значение выходного сигнала в установившемся режиме.
8)по полученному графику переходной характеристике y(t) определить показатели качества переходного процесса: время установления, время первого максимума, время регулирования, перерегулирование;
Все пункты контрольной работы выполнять вручную, без использования ПЭВМ;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|||
|
|
W1(P) |
|
W2(P) |
|
|
W3(P) |
|
W4(p) |
|
|
||||||||||||
K |
|
T1 p + K01 |
|
|
|
K2 |
|
|
|
|
K3 |
|
|
K |
|
T4 p +1 |
|
||||||
1 |
|
(τ1 p +1) p |
|
τ2 p +1 |
|
|
τ3 p +1 |
|
|
4 τ4 p +1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|||
|
|
|
|
|
|
|
|
|
|
|
варианты |
|
|
|
|
|
|
|
|
||||
|
|
1 |
2 |
|
3 |
4 |
5 |
6 |
|
7 |
|
8 |
|
9 |
|
0 |
|
||||||
K1 |
|
10 |
9 |
|
9 |
8 |
8 |
7 |
|
7 |
|
10 |
|
10 |
|
12 |
|
||||||
T1 |
|
1 |
1 |
|
1 |
1 |
0.5 |
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
||||||
τ1 |
|
0.6 |
1.2 |
0.8 |
1.6 |
1.0 |
0 |
|
1.8 |
|
0 |
|
1.4 |
|
0 |
|
|||||||
К01 |
|
0 |
1 |
|
1 |
1 |
1 |
1 |
|
0 |
|
1 |
|
0 |
|
0 |
|
||||||
K2 |
|
5.0 |
0.6 |
9 |
0.8 |
0.7 |
6.0 |
|
4.0 |
|
5.0 |
0.5 |
3.0 |
|
|||||||||
τ2 |
|
0.1 |
0 |
|
0.2 |
0 |
0 |
0.1 |
|
0.2 |
|
0.3 |
0 |
|
0.5 |
|
|||||||
Κ3 |
|
5 |
10 |
|
6 |
8 |
5 |
4 |
|
3 |
|
2 |
|
9 |
|
7 |
|
||||||
τ3 |
|
0 |
0.08 |
0 |
0 |
0.2 |
0.05 |
|
0 |
|
0 |
|
0.1 |
0.01 |
|
||||||||
Κ4 |
|
1 |
2 |
|
5 |
8 |
3 |
4 |
|
10 |
|
1 |
|
4 |
|
0.5 |
|
||||||
Τ4 |
|
0.08 |
0 |
|
0 |
0 |
0 |
0 |
|
0.05 |
0 |
|
0 |
|
0 |
|
|||||||
τ4 |
|
0.01 |
0 |
|
0 |
0.3 |
0 |
0 |
|
0.02 |
0.1 |
1.8 |
0.1 |
|
|||||||||
Κ5 |
|
0.02 |
0.01 |
0.03 |
0.1 |
0.03 |
0.2 |
0.01 |
0.1 |
0.3 |
0.4 |
|
|||||||||||

Рисунок 1
Рисунок 2
Рисунок 3
Рисунок 4
Рисунок 5

Рисунок 6
Рисунок 7
Рисунок 8
Рисунок 9
Рисунок 10

ПРИЛОЖЕНИЕ 1
МЕТОД ПРИБЛИЖЕННОГО АНАЛИТИЧЕСКОГО ОПРЕДЕЛЕНИЯ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ
Для нахождения переходного процесса в системе необходимо знать корни характеристического уравнения. Поэтому приобретает практическое значение умение определять корни уравнения системы, имеющей любой достаточно высокий порядок.
Положим, что имеется характеристическое уравнение вида: dnpn+dn-1pn-1+...+d2p2+d1p+d0=0.
В усеченном уравнении, образованном из трех последних
членов характеристического уравнения: d2p2+d1p+d0=0,
определяют корни p01 и p02. Если эти корни оказываются вещественными, то определяют один вещественный корень характеристического уравнения, а если комплексными — определяют первую комплексную пару корней.
Вычисление вещественного корня
Перед вычислениями характеристическое уравнение норми-
руют и приводят к виду: pn+Dn-1pn-1+...+D2p2+D1p+D0=0.
Процесс вычисления первого вещественного корня состоит в следующем: отбрасывают старшие члены уравнения и задают
* |
D0 |
первое приближенное значение искомого корня в виде p1 |
=-D1 |
, далее делят характеристическое уравнение на разность (p—p1*) до тех пор, пока в остатке не окажется двучлен вида D1*p+D0, который нельзя разделить без остатка на разность (p—p1*).
Вкачестве второго приближения для первого искомого
** |
|
D0 |
|
корня берут значение p1 |
=- |
D1* |
, определяемое как отношение |
|
- |
D0 |
|
|
|
|
|
|
||
вида |
D1* |
. Затем характеристическое уравнение делят на |
||||||||
разность |
|
(p—p1**) до |
тех пор, пока не |
останется |
двучлен |
|||||
|
** |
|
|
|
|
*** |
|
D0 |
||
вида |
D1 |
p+D0. Берут |
третье приближение |
корня p1 |
|
=- |
D1** |
, |
||
D0
определяемое выражением -D1**. Чаще всего достаточно двух—
трех приближений для того, чтобы остаток от деления характеристического уравнения на соответствующую разность (p—p1***) был бы близок к нулю. Это означает, что первый искомый корень p1 определен, после чего степень характе-

ристического уравнения понижается на единицу.
Указанная процедура повторяется применительно к новому уравнению пониженного порядка до тех пор, пока не будет найден следующий корень. Аналогичным путем находят все искомые корни характеристического уравнения.
Пример
Характеристическое уравнение имеет вид:
р3+13р2+39р+27=0.
В первом приближении
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
D0 |
27 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
p1 |
=-D1=39=-0,7. |
|
|
|
|
||||||||||||||||
Уточняем корень делением уравнения на выражение (p-p1*). |
|||||||||||||||||||||||||||||||
|
p3 |
+ |
13 |
p2 |
+ |
|
39 |
p |
+ |
27 |
|
|
|
p |
+ |
|
0,7 |
|
|
|
|
|
|||||||||
|
p3 |
+ |
0,7 |
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
+ |
|
12,3 |
p + |
30,4 |
|
|
||
|
|
|
12,3 |
p2 |
+ |
|
39 |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
12,3 |
p2 |
+ |
|
8,6 |
p |
|
+ |
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
30,4 |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
30,4 |
p |
+ |
21,3 |
|
|
(остаток) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5,7 |
|
|
|
|
|
|
|
|||||||||
Во втором приближении |
|
|
|
|
|
|
D0 |
27 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
** |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
р1 |
|
=- |
D1* |
=- |
|
|
|
=-0,89. |
|
|
|
|||||||||||
Уточняем |
|
|
|
|
|
30,4 |
выражение |
(p- |
|||||||||||||||||||||||
корень делением |
уравнения |
на |
|||||||||||||||||||||||||||||
p1**). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p3 |
+ |
13 |
p2 |
+ |
|
39 |
|
|
p |
+ |
27 |
|
|
|
p |
+ |
0,9 |
|
|
|
|
|||||||||
|
p3 |
+ |
0,9 |
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
+ |
12,1 |
p |
+ 28,11 |
|
|
||
|
|
|
12,1 |
p2 |
+ |
|
39 |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
12,1 |
p2 |
+ |
|
10,89 |
|
|
p |
+ |
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
28,11 |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
28,11 |
|
|
p |
+ |
25,3 |
|
|
(остаток) |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,7 |
|
|
|
|
|
|
|||||||
|
В третьем приближении |
|
D0 |
27 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
*** |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
р1 |
=- |
D1** |
=- |
|
|
=-0,96. |
|
|
|
|||||||||||||
|
Уточняем |
|
|
|
|
28,11 |
выражение |
(p- |
|||||||||||||||||||||||
|
корень делением |
уравнения |
на |
||||||||||||||||||||||||||||
p1***). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p3 |
+ |
13 |
p2 |
+ |
39 |
|
|
|
p |
+ |
27 |
|
|
|
|
p |
+ |
0,96 |
|
|
|
|||||||||
|
p3 |
+ |
0,96 |
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
+ |
12,04 |
p + 27,44 |
|
|||
|
|
|
12,04 |
p2 |
|
+ |
39 |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
12,04 |
p2 |
+ |
11,56 |
|
|
|
p |
|
|
+ |
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
27,44 |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
27,44 |
|
|
|
p |
+ |
26,34 |
|
(остаток) |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,66 |
|
|
|
|
|
||||||||

В четвертом приближении
**** |
|
D0 |
27 |
≈ |
|
|
р1 |
=- |
D1*** |
=- |
|
|
-1. |
27,44 |
|
|||||
Итак, один вещественный корень р1=-1.
Разделим исходное уравнение на делитель (p-p1):
p3 |
+ 13 |
p2 |
+ 39 p + 27 |
|
p + 1 |
|||||
|
||||||||||
p3 |
+ 1 |
p2 |
|
|
|
|
|
|
p2 + 12 p + 27 |
|
|
12 |
p2 |
+ |
39 |
p |
|
|
|
|
|
|
|
12 |
p2 |
+ |
12 |
p |
+ |
27 |
|
|
|
|
|
|
|
27 |
p |
|
|
||
|
|
|
|
|
27 |
p |
+ |
27 |
|
(остаток) |
|
|
|
|
|
|
|
|
0 |
|
|
Два другие корня определяются из квадратного уравне-
ния p2+12р+27=0:
p2=-3; p3=-9.
Таким образом корни характеристического полинома
р3+13р2+39р+27 равны p1=-1; p2=-3; p3=-9.
Значит характеристический полином можно представить в виде р3+13р2+39р+27=(р+1)(р+3)(р+9).
При четном порядке характеристического уравнения действия при нахождении корней остаются прежними, с той лишь разницей, что первое деление производится на квадратный трехчлен. В дальнейшем его значение уточняется.
Пусть имеется уравнение
р4+6р3+18р2+24р+16=0.
Выделим квадратный трехчлен в качестве первого приближения:
р2+2418р+1618=р2+1,33р+0,889.
р4 |
+ 6,00 |
p3 |
+ 18,00 |
p2 |
+ 24,00 |
p + 16 |
p2 |
+ 1,33 |
р + 0,889 |
|||
р4 |
+ 1,33 |
p3 |
+ 0,889 |
p2 |
|
|
|
p2 |
+ 4,67 |
p + 10,89 |
||
|
4,67 |
р3 |
+ 17,11 |
p2 |
+ 24,00 |
p |
|
|
|
|
||
|
|
4,67 |
р3 |
+ 6,22 |
p2 |
+ 4,15 |
p |
|
|
|
||
|
|
|
|
10,89 |
р2 |
+ 19,85 |
p + 16 |
|
|
|
||
|
|
|
|
|
10,89 |
р2 |
+ 14,49 |
p + 9,67 |
(остаток) |
|
||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
5,36 |
р + 6,33 |
|
|||
Второе приближение:
|
10,89р2+19,85р+16; |
|||
2 |
19,85 |
16 |
2 |
|
р |
+10,89р+ |
|
=р |
+1,82р+1,47. |
10,89 |
||||

р4 |
+ |
6,00 |
p3 |
+ |
18,00 |
p2 |
+ |
24,00 |
p |
+ |
16 |
|
p2 |
+ |
1,82 |
р |
+ |
1,47 |
|
||||||||||||||||||
р4 |
+ |
1,82 |
p3 |
+ |
1,47 |
p2 |
|
|
|
|
|
|
p2 |
+ |
4,18 |
p |
+ |
8,93 |
|
|
4,18 |
р3 |
+ |
16,53 |
p2 |
+ |
24,00 |
p |
|
|
|
|
|
|
|
|
|
|
|
4,18 |
р3 |
+ |
7,60 |
p2 |
+ |
6,14 |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8,93 |
р2 |
+ |
17,86 |
p |
+ |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
8,93 |
р2 |
+ |
16,25 |
p |
+ |
13,1 |
|
(остаток) |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1,61 |
р |
+ |
2,9 |
|
|
|
|
|||
Третье приближение:
8,93р2+17,86р+16;
2 17,86 16 2 р + 8,93 р+8,93=р +2р+1,79.
р4 |
+ |
6,00 |
p3 |
+ |
18,00 |
p2 |
+ |
24,00 |
p |
+ |
16 |
|
p2 |
+ |
2 |
р |
+ |
1,79 |
|
||||||||||||||||||
р4 |
+ |
2,00 |
p3 |
+ |
1,79 |
p2 |
|
|
|
|
|
|
p2 |
+ |
4,00 |
p |
+ |
8,21 |
|
|
4,00 |
р3 |
+ |
16,21 |
p2 |
+ |
24,00 |
p |
|
|
|
|
|
|
|
|
|
|
|
4,00 |
р3 |
+ |
8,00 |
p2 |
+ |
7,16 |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8,21 |
р2 |
+ |
16,84 |
p |
+ |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
8,21 |
р2 |
+ |
16,42 |
p |
+ |
14,7 |
|
(остаток) |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0,42 |
р |
+ |
1,3 |
|
|
|
|
|||
Четвертое приближение:
|
|
|
|
|
|
|
|
8,21р2+16,84р+16; |
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
16,84 |
16 |
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
р |
+ |
8,21 |
р+ |
|
=р |
+2,05р+1,95. |
|
|
|
|||||||
|
|
|
|
|
8,21 |
|
|
|
|||||||||||||
р4 |
+ |
6,00 |
p3 |
+ |
18,00 |
p2 |
+ |
24,00 |
p |
+ |
16 |
|
p2 |
+ |
2,05 |
р |
+ |
1,95 |
|||
|
|||||||||||||||||||||
р4 |
+ |
2,05 |
p3 |
+ |
1,95 |
p2 |
|
|
|
|
|
|
|
|
p2 |
+ |
3,95 |
p |
+ |
7,95 |
|
|
|
3,95 |
р3 |
+ |
16,05 |
p2 |
+ |
24,00 |
p |
|
|
|
|
|
|
|
|
|
|||
|
|
3,95 |
р3 |
+ |
8,10 |
p2 |
+ |
7,70 |
p |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
7,95 |
р2 |
+ |
16,30 |
p |
+ |
16 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
7,95 |
р2 |
+ |
16,30 |
p |
+ |
15,7 |
|
(остаток) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||||||
Пятое приближение: |
|
|
|
|
|
|
0,3 |
|
|
|
|
||||||||||
р2+2,05р+2,01. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Различие между четвертым и пятым приближениями очень мало, поэтому ограничившись четвертым приближением, представляем исходное уравнение в виде:
(p2+2,05р+1,95)(p2+3,95p+7,95)=0.
Отсюда определяем корни:
р1,2=-1,03±j0,95; p3,4=-1,98±j2,02.

ПРИЛОЖЕНИЕ 2
НАХОЖДЕНИЕ КРИВОЙ ПЕРЕХОДНОГО ПРОЦЕССА С ИСПОЛЬЗОВАНИЕМ ВТОРОЙ ТЕОРЕМЫ РАЗЛОЖЕНИЯ
Если функция Y(p) есть правильная несократимая рациональная дробь, т. е.:
F1(p) Y(p)=F2(p),
то оригинал для Y(p) можно найти, разложив дробь Y(p) на простейшие и воспользовавшись формулой
Ai n Þ A epit tn-1 .
(p-pi) i (n-1)!
Вторая теорема разложения устанавливает формулу оригинала y(t) для дроби Y(p).
Рассмотрим два случая.
F1(p)
1. Если Y(p)=F2(p) (где F1(р), F2(р) — полиномы от р)
— правильная несократимая рациональная дробь и все корни, р1, р2,..., рn знаменателя F2(р) — простые, то оригинал y(t) для Y(p) выражается формулой
n |
F1(pk) |
e |
pkt |
|
|
|
’ |
|
|
édF2(p)ù |
|
|||||||||||||||
y(t)= å |
|
|
|
|
|
|
, где F2 |
(pk)=ê |
|
|
|
|
|
ú |
|
|
|
|||||||||
' |
|
|
|
|
|
|
|
dp |
|
|||||||||||||||||
k = 1 F2(pk) |
|
|
|
|
|
|
|
|
|
ë |
|
|
û p = pk |
|
||||||||||||
Доказательство. Разложив дробь Y(p) на простейшие, |
||||||||||||||||||||||||||
получим: |
|
A1 |
|
|
A2 |
|
|
An |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Y(p)=F1(p)= |
+ |
+...+ |
|
. |
|
|
|
|
|
|
|
|
|
(*) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
F2(p) p-p1 |
|
p-p2 |
p-pn |
|
|
|
|
|
|
|
|
|||||||||||||||
Оригинал y(t) для Y(p), очевидно, будет иметь вид |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
(**) |
|||
y(t)=A1 ep1t +A2 ep2t +...+An epnt = å Ak epkt . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 1 |
|
|
|
|
|
|
|
|
|||
Чтобы определить A1 умножим равенство (*) на p-p1 и |
||||||||||||||||||||||||||
перейдем к пределу p®p1. Это даст |
|
|
|
|
A2 |
|
|
|
|
An |
|
|||||||||||||||
F1(p)(p-p1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
limp→p1 F2(p) |
=limp→p1[A1+(p-p1)( |
|
+...+ |
|
|
)]=A1; |
||||||||||||||||||||
p-p2 |
p-pn |
|||||||||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
F1(p) |
|
|
|
|
F1(p1) |
|
||||||
F1(p)(p-p1) |
|
|
|
|
|
|
|
|
||||||||||||||||||
A1=limp→p1 |
F2(p) |
|
|
=limp→p1 |
|
|
|
= |
F2'(p1) |
. |
||||||||||||||||
|
|
F2(p)-F2(p1) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p-p1 |
|
|
|
|
|
|
|
|
|||
Здесь надо иметь в виду, что F2(р1)=0. |
|
|
|
|
|
|
|
|
||||||||||||||||||
Аналогично найдем |
F1(p2) |
|
|
|
|
F1(pn) |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
A2= |
F2'(p2) |
,..., An= |
F2'(pn) |
. |
|
|
|
|
|
|
|
|
|||||||||||||
Подставляя найденные значения А1, A2,..., An в равенство (**), получим:
