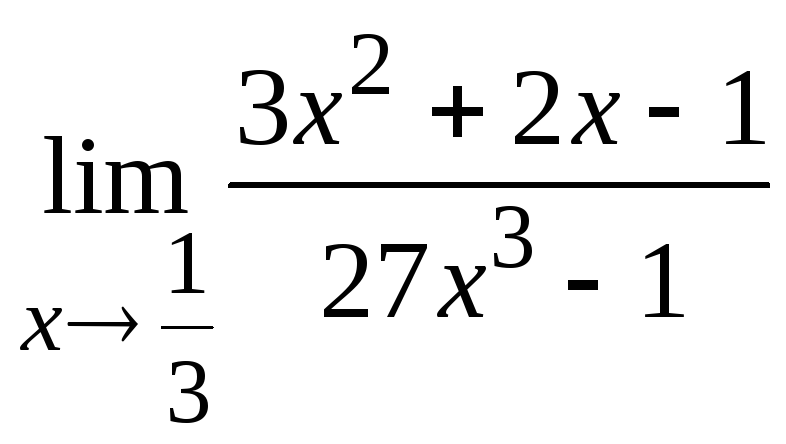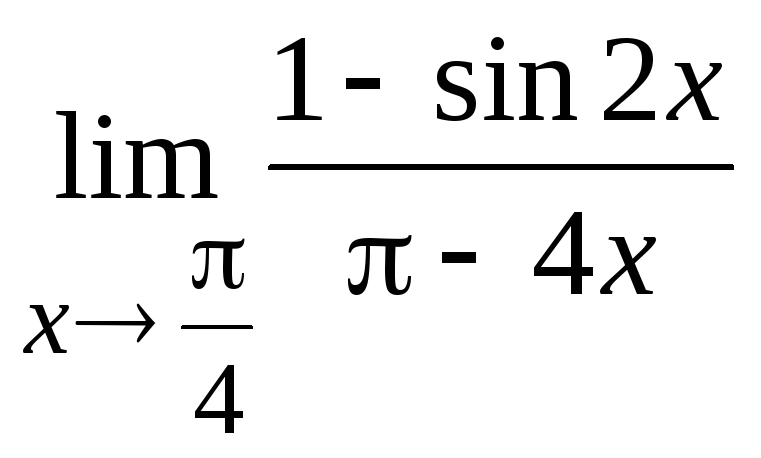1 Правила выполнения и оформления контрольной работы
При оформлении контрольной работы следует строго придерживаться указанных ниже правил. Работа, выполненная без соблюдения этих правил, не зачитывается и возвращается студенту для переработки.
1 Контрольную работу следует выполнять в отдельной тетради, на обложке которой студент должен разборчиво написать номер контрольной работы, название дисциплины, указать свою группу, фамилию, инициалы и номер зачетной книжки.
2 Решение задач необходимо проводить в последовательности, указанной в контрольной работе. При этом условие каждой задачи нужно полностью переписывать перед ее решением. В тетради обязательно оставить поля.
3 Решение каждой задачи следует излагать подробно, давать необходимые пояснения по ходу решения со ссылкой на используемые формулы. В конце контрольной работы необходимо указать использованную при выполнении контрольной работы литературу.
4 После получения прорецензированной работы, как зачтенной, так и незачтенной, следует исправить отмеченные ошибки и недочеты и выполнить все рекомендации рецензента. Незачтенные задания необходимо выполнить заново. Вносить исправления в сам текст работы после рецензирования запрещается.
5 На повторную проверку следует обязательно предоставлять и ранее прорецензированную работу.
Номера вариантов задач для контрольной работы следует выбирать по схеме:
- номер варианта соответствует числу из двух последних цифр, если это число не более 30;
- если это число больше 30, номер варианта следует брать равным результату вычитания из этого числа 30 до получения числа, не большего 30;
- если две последние цифры 00, то номер варианта равен 10.
Например:
а) номер зачетки заканчивается цифрами 03- вариант задания равен 3;
б) номер зачетки заканчивается цифрами 66- вариант задания равен 6.
Задание 1
Дана система линейных алгебраических уравнений (СЛАУ). Требуется:
1) решить СЛАУ по формулам Крамера;
2) записать СЛАУ в матричной форме и решить ее матричным способом;
3) решить СЛАУ методом Гаусса.
1
 2
2
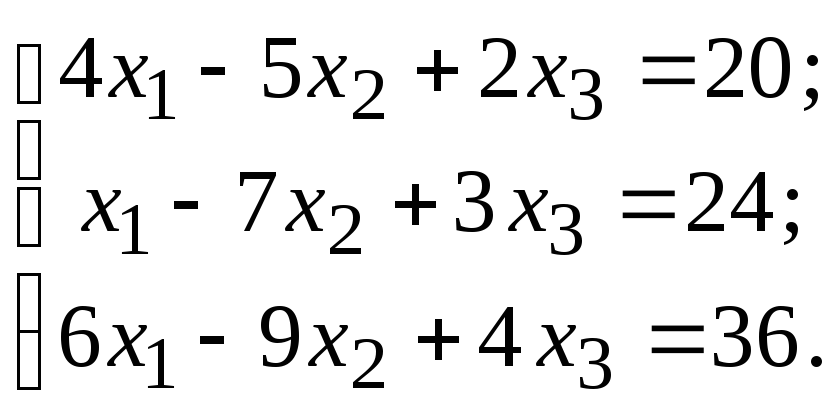 3
3

4
 5
5
 6
6

7
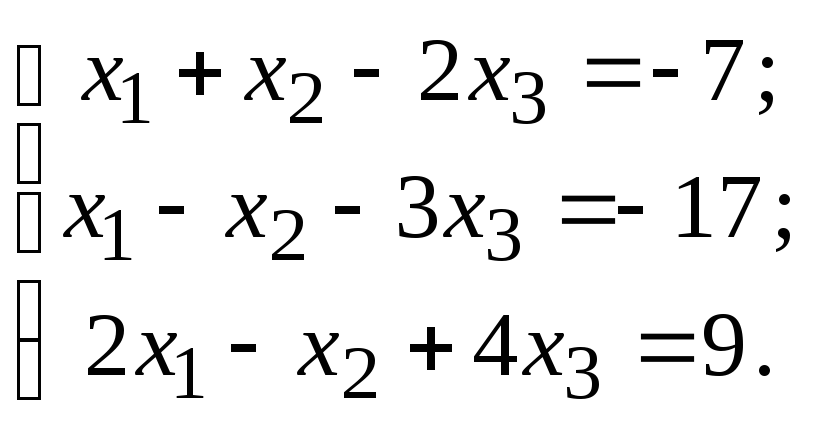 8
8
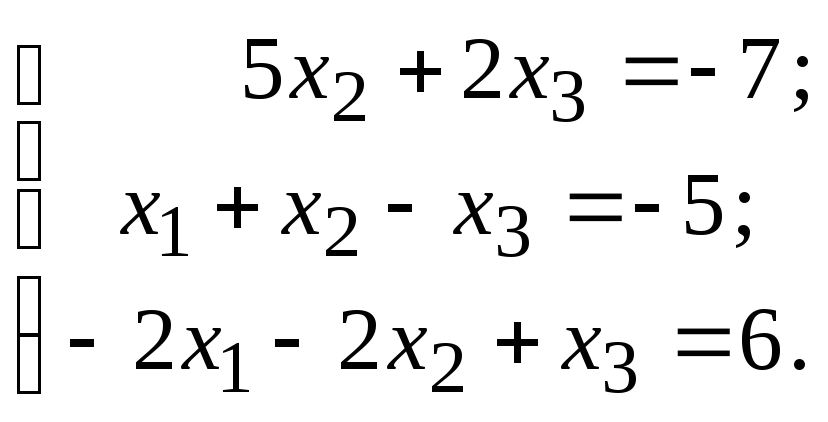 9
9
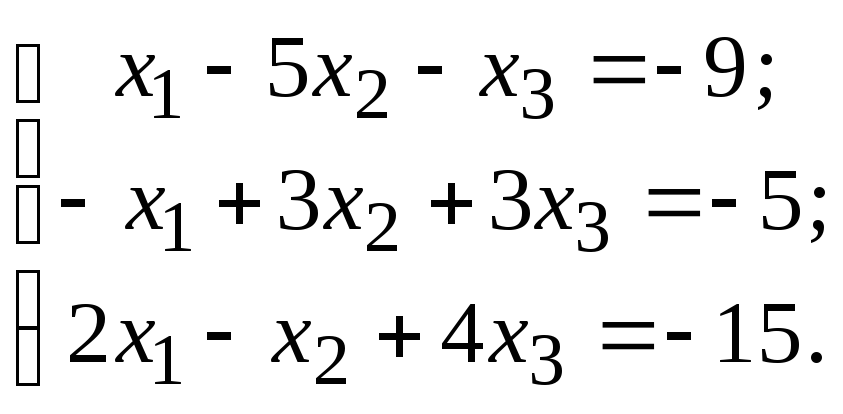
10
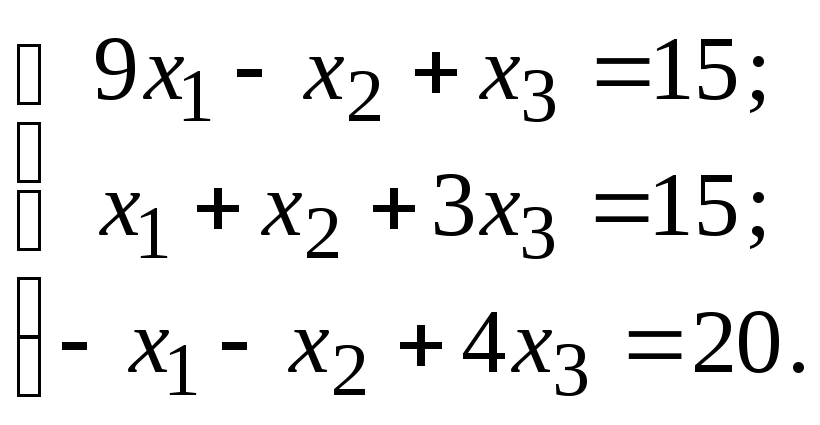 11
11
 12
12

13
 14
14
 15
15

16
 17
17
 18
18

19
 20
20
 21
21
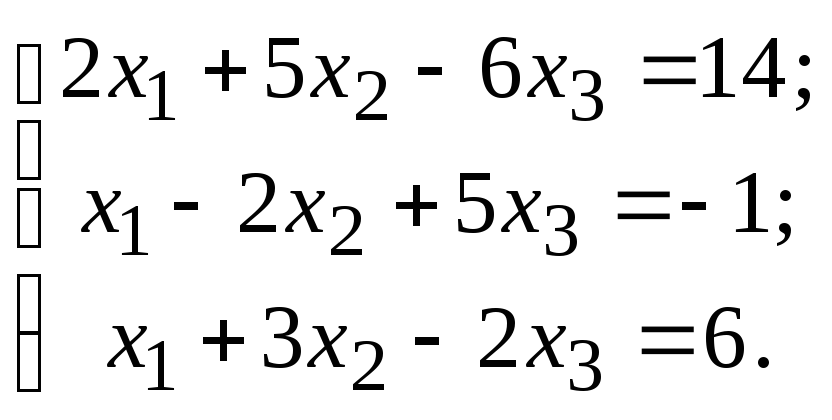
22
 23
23
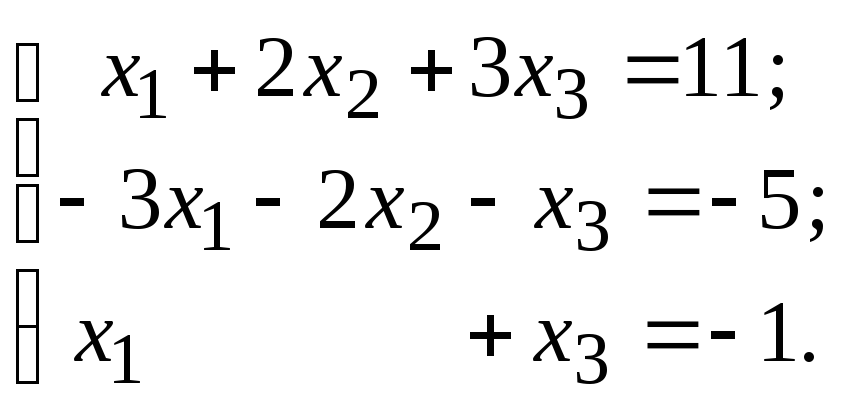 24
24

25
 26
26
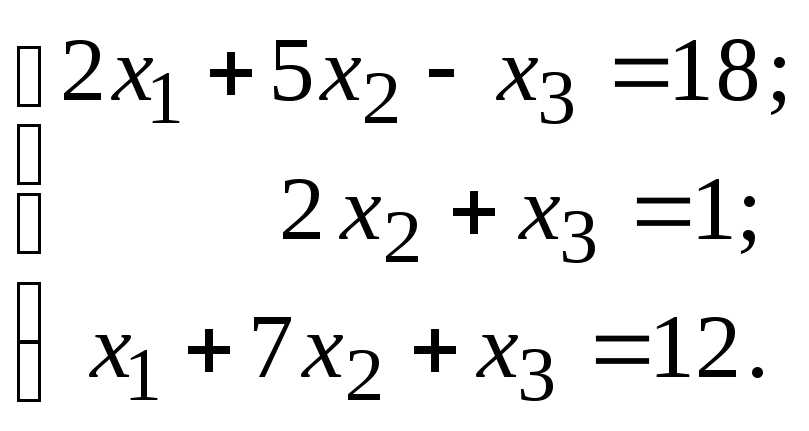 27
27

28
 29
29
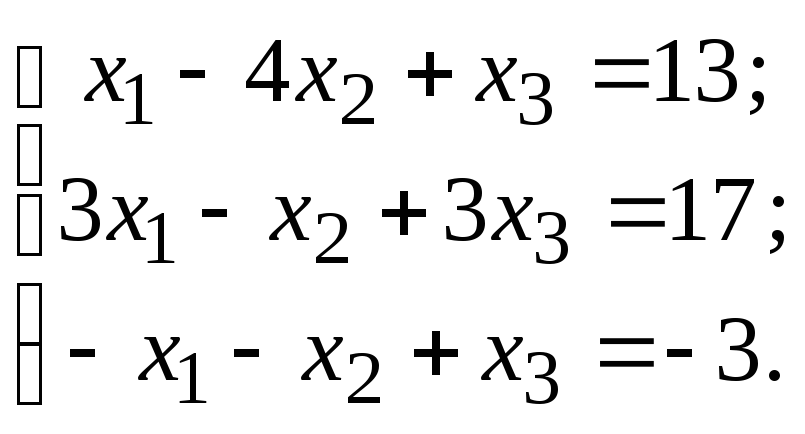 30
30

Задание 2
Даны
вершины треугольника АВС:
![]()
![]()
![]() Найти:
Найти:
1) уравнение стороны АВ;
2) уравнение высоты СН и ее длину;
3) уравнение медианы АМ и ее длину;
4) точку N пересечения медианы АМ и высоты СН;
5) уравнение прямой, проходящей через вершину С параллельно стороне АВ;
6) внутренний угол при вершине А.
Таблица 1 - Варианты условий для задания 2
|
Номер варианта |
|
|
|
|
Номер варианта |
|
|
|
|
1 |
(3; 1) |
(0; -2) |
(-1; 2) |
|
16 |
(1; 4) |
(0; -4) |
(-2; 1) |
|
2 |
(0; 1) |
(5; -3) |
(-1; -1) |
|
17 |
(-2; -2) |
(0; 2) |
(4; 0) |
|
3 |
(-4; -1) |
(3; -11) |
(0; 1) |
|
18 |
(1; 1) |
(-1; 5) |
(-4; 3) |
|
4 |
(3; 2) |
(2; -1) |
(-2; 1) |
|
19 |
(-3; 0) |
(2; 3) |
(2; -2) |
|
5 |
(-3; -1) |
(3; 2) |
(4; -3) |
|
20 |
(3; 6) |
(-2; 4) |
(0; 0) |
|
6 |
(0; -4) |
(-2; 1) |
(1; 4) |
|
21 |
(0; -2) |
(-1; 2) |
(3; 1) |
|
7 |
(0; 2) |
(4; 0) |
(-2; -2) |
|
22 |
(5; -3) |
(-1; -1) |
(0; 1) |
|
8 |
(-1; 5) |
(-4; 3) |
(1; 1) |
|
23 |
(3; -11) |
(0; 1) |
(-4; -1) |
|
9 |
(2; 3) |
(2; -2) |
(-3; 0) |
|
24 |
(2; -1) |
(-2; 1) |
(3; 2) |
|
10 |
(-2; 4) |
(0; 0) |
(3; 6) |
|
25 |
(3; 2) |
(4; -3) |
(-3; -1) |
|
11 |
(-1; 2) |
(3; 1) |
(0; -2) |
|
26 |
(-2; 1) |
(1; 4) |
(0; -4) |
|
12 |
(-1; -1) |
(0; 1) |
(5; -3) |
|
27 |
(4; 0) |
(-2; -2) |
(0; 2) |
|
13 |
(0; 1) |
(-4; -1) |
(3; -11) |
|
28 |
(-4; 3) |
(1; 1) |
(-1; 5) |
|
14 |
(-2; 1) |
(3; 2) |
(2; -1) |
|
29 |
(2; -2) |
(-3; 0) |
(2; 3) |
|
15 |
(4; -3) |
(-3; -1) |
(3; 2) |
|
30 |
(0; 0) |
(3; 6) |
(-2; 4) |
Задание 3
Найти пределы функций, не пользуясь правилом Лопиталя.
Таблица 2 - Варианты условий для задания 3
|
Номер варианта |
а |
б |
в |
г |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
7 |
|
|
|
|
|
8 |
|
|
|
|
|
9 |
|
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
12 |
|
|
|
|
Продолжение таблицы 2
|
Номер варианта |
а |
б |
в |
г |
|||
|
13 |
|
|
|
|
|||
|
14 |
|
|
|
|
|||
|
15 |
|
|
|
|
|||
|
16 |
|
|
|
|
|||
|
17 |
|
|
|
|
|||
|
18 |
|
|
|
|
|||
|
19 |
|
|
|
|
|||
|
20 |
|
|
|
|
|||
|
21 |
|
|
|
|
|||
|
22 |
|
|
|
|
|||
|
23 |
|
|
|
|
|||
|
24 |
|
|
|
|
|||
Продолжение таблицы 2
|
Номер варианта |
а |
б |
в |
г |
|
25 |
|
|
|
|
|
26 |
|
|
|
|
|
27 |
|
|
|
|
|
28 |
|
|
|
|
|
29 |
|
|
|
|
|
30
|
|
|
|
|
Задание 4. Найти:
а)
производную и дифференциал функции
![]() в точке
в точке
![]() ;
;
б)
при помощи логарифмического
дифференцирования производную функции
![]()
в)
производную функции
![]() ,
заданной неявно уравнением
,
заданной неявно уравнением
![]() .
.
Таблица 3 - Варианты условий для задания 4
|
Номер варианта |
а |
б |
в |
|
1 |
|
|
|
|
2 |
|
|
|
Продолжение таблицы 3
|
Номер варианта |
а |
б |
в |
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
Продолжение таблицы 3
|
Номер варианта |
а |
б |
в |
|
19 |
|
|
|
|
20 |
|
|
|
|
21 |
|
|
|
|
22 |
|
|
|
|
23 |
|
|
|
|
24 |
|
|
|
|
25 |
|
|
|
|
26 |
|
|
|
|
27 |
|
|
|
|
28 |
|
|
|
|
29 |
|
|
|
|
30 |
|
|
|
Задание 5
Исследовать
методами дифференциального исчисления
функцию
![]() и построить ее график.
и построить ее график.
Таблица 4 - Варианты условий для задания 5
|
Номер варианта |
|
Номер варианта |
|
Номер варианта |
|
|
1 |
|
11 |
|
21 |
|
Продолжение таблицы 4
|
Номер варианта |
|
Номер варианта |
|
Номер варианта |
|
|
|
2 |
|
12 |
|
22 |
|
|
|
3 |
|
13 |
|
23 |
|
|
|
4 |
|
14 |
|
24 |
|
|
|
5 |
|
15 |
|
25 |
|
|
|
6 |
|
16 |
|
26 |
|
|
|
7 |
|
17 |
|
27 |
|
|
|
8 |
|
18 |
|
28 |
|
|
|
9 |
|
19 |
|
29 |
|
|
|
10 |
|
20 |
|
30 |
|
|
Задание 6
a), б) Найти неопределенный интеграл;
в) вычислить определенный интеграл.
Таблица 5 - Варианты условий для задания 6
|
Номер варианта |
а |
б |
в |
|
1 |
|
|
|
Продолжение таблицы 5
|
Номер варианта |
а |
б |
в |
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
Продолжение таблицы 5
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
19 |
|
|
|
|
20 |
|
|
|
|
21 |
|
|
|
|
22 |
|
|
|
|
23 |
|
|
|
|
24 |
|
|
|
|
25 |
|
|
|
|
26 |
|
|
|
Продолжение таблицы 5
|
27 |
|
|
|
|
28 |
|
|
|
|
29 |
|
|
|
|
30 |
|
|
|
Задание 7
Дана
функция
![]() ,
точки
,
точки
![]() и
и
![]() .
.
Найти:
1) частные производные и полный дифференциал данной функции;
2) производную
функции в точке
![]() по направлению вектора
по направлению вектора
![]() и градиент функции в точке
и градиент функции в точке
![]()
Таблица 6 – Варианты условий для задания 7
|
Номер варианта |
Условие задачи |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
Продолжение таблицы 6
|
Номер варианта |
Условие задачи |
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
Продолжение таблицы 6
|
Номер варианта |
Условие задачи |
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|