- •Белорусско-российский университет
- •1.2.Определители и их свойства
- •1.3.Системы линейных алгебраических уравнений
- •1.4.Формулы Крамера
- •1.5.Общий алгоритм решения системы линейных уравнений
- •1.6.Матричный метод решения линейной системы.
- •1.7.Понятие о приближенных методах решения линейных систем
- •1.8.Линейное, евклидово и нормированное пространства.
- •1.9.Линейные операторы и матрицы
- •1.10.Задача о собственных значениях
- •1.11.Свойства симметрических матриц
- •1.12.Квадратичные формы и их приведение к каноническому виду
- •Векторная алгебра
- •2.2.Скалярное произведение векторов
- •2.3.Векторное произведение векторов
- •2.4.Смешанное произведение векторов
- •2.5.Типовые задачи, решаемые средствами векторной алгебры
- •3.Аналитическая геометрия.
- •3.1.Уравнения линий и поверхностей
- •3.2.Уравнение 1-й степени на плоскости
- •3.3.Уравнения первой степени в пространстве
- •3.4.Уравнения первой степени в пространстве
- •3.5.Уравнения 2-й степени на плоскости
- •3.6.Уравнения 2-й степени в пространстве
- •3.7.Цилиндры и поверхности вращения
- •3.8.Упрощение кривых 2-го порядка
1.11.Свойства симметрических матриц
Опред. Матрицу называют симметрической, если aij=aji. Для всехi,j.
Теорема. Собственные значения симметрической матрицы – действительные числа, собственные векторы – ортогональны.
Док. Ограничимся матрицей размерности
2. Имеем А= .
Характеристическое уравнение имеет
вид к2-(а11+а22)+(а11а22-а122)=0.
Его дискриминант равен
(а11+а22)2-4(а11а22-а122)=
(а11-а22)2+4а122
.
Характеристическое уравнение имеет
вид к2-(а11+а22)+(а11а22-а122)=0.
Его дискриминант равен
(а11+а22)2-4(а11а22-а122)=
(а11-а22)2+4а122![]() 0.
А это значит – корни квадратного
уравнения действительные числа.
0.
А это значит – корни квадратного
уравнения действительные числа.
Рассмотрим случай разных корней . Тогда
по Виету имеем к1+к2= а11+а22,
и к1к2= а11а22-а122
.С другой стороны для к1найдем
собственный вектор
![]() 1из системы
1из системы
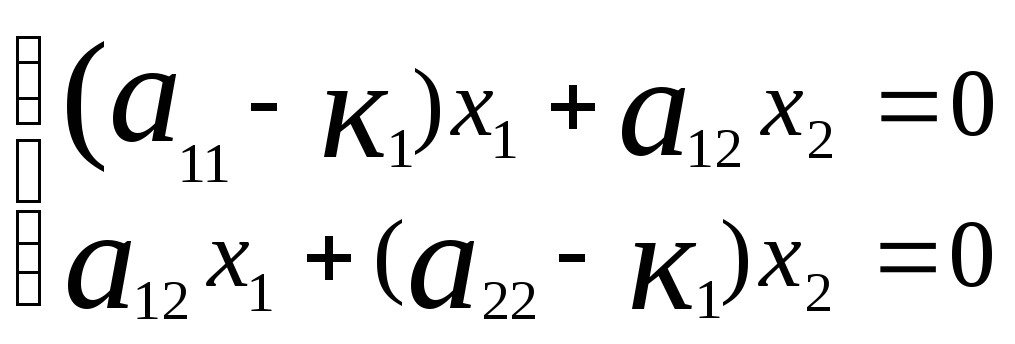 Как известно, в этой системе одно из
уравнений лишнее, т.к.rancA=1.
И потому мы отбросим , например, второе
уравнение в системе и возьмем х2=а11-к1. Тогда получим собственный вектор
Как известно, в этой системе одно из
уравнений лишнее, т.к.rancA=1.
И потому мы отбросим , например, второе
уравнение в системе и возьмем х2=а11-к1. Тогда получим собственный вектор
![]() 1=(-а12
а11-к1)T. Из аналогичных рассуждений найдем
1=(-а12
а11-к1)T. Из аналогичных рассуждений найдем
![]() 2=(-а12
а11-к2)T. Теперь вычислим их скалярное произведение
2=(-а12
а11-к2)T. Теперь вычислим их скалярное произведение
![]() 1
1![]() 2=а122+(а11-к1)(а11-к2)=
а122+а112- а11(а11+
а22)+ а11а22-а122=0.
2=а122+(а11-к1)(а11-к2)=
а122+а112- а11(а11+
а22)+ а11а22-а122=0.
Если же корни равны, то это происходит
только тогда, когда одновременно а12=0
и а11- а22=0. Но это может быть
только если к1= к2= а11.
Но тогда в качестве
![]() 1можно взять
1можно взять
![]() 1=(1
0)T,а в качестве
1=(1
0)T,а в качестве
![]() 2можно взять
2можно взять
![]() 2=(0
1)T . И все
равно они будут ортогональны.
2=(0
1)T . И все
равно они будут ортогональны.
1.12.Квадратичные формы и их приведение к каноническому виду
Пусть в ЛП размерности 2 задан
![]() =(
х1 х2)T в нормированном евклидовом
ортогональном базисе i,j.
=(
х1 х2)T в нормированном евклидовом
ортогональном базисе i,j.
Опред. Выражение ф(х1,х2)= а11х12+2а12 х1 х2
+а22х22=0 где aij - действительные числа,
называют квадратичной формой двух
переменных х1,х2. Ее можно записать иначе
ф(х1,х2)= (а11х1+а12х2) х2+(а12 х1+а22х2)х2. Затем,
используя умножение матрицы на вектор
получить ф(х1,х2)=
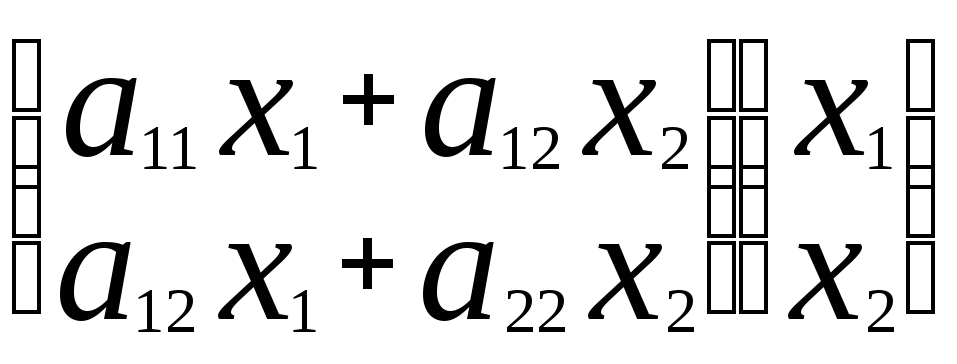 =((
=((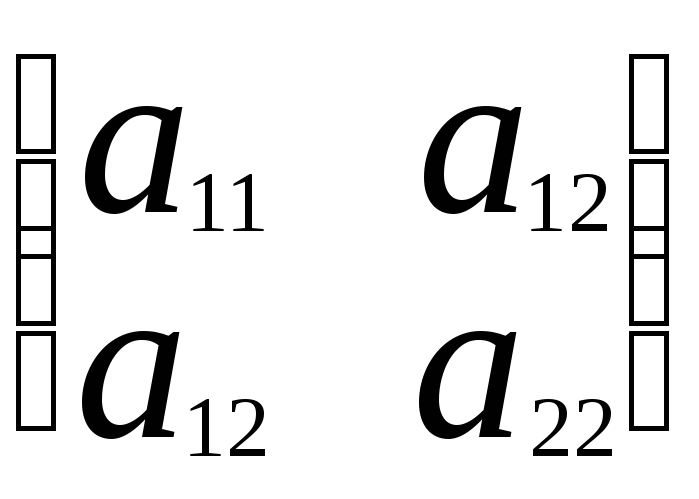
![]() ),
),![]() )=(Ах,х), причем матрица А – симметрическая
и , как известно, ее ее собственные
векторы ортогональны. Пусть это будут
векторы
)=(Ах,х), причем матрица А – симметрическая
и , как известно, ее ее собственные
векторы ортогональны. Пусть это будут
векторы
![]() 1
и
1
и
![]() 2
. Тогда их можно нормировать и принять
в качестве базисных в ортонормированном
евклидовом ЛП. Построим единичные
векторы в новом базисе (базисе собственных
векторов матрицы А). Получаем
2
. Тогда их можно нормировать и принять
в качестве базисных в ортонормированном
евклидовом ЛП. Построим единичные
векторы в новом базисе (базисе собственных
векторов матрицы А). Получаем
![]() и
и
![]() - новые единичные . И в этом новом базисе
вектор
- новые единичные . И в этом новом базисе
вектор
![]() =(
х’1 х’2)T. Но в этом случае и квадратичная
форма примет новый вид ф(х1,х2)= (А(х’1
=(
х’1 х’2)T. Но в этом случае и квадратичная
форма примет новый вид ф(х1,х2)= (А(х’1![]() +
х’2
+
х’2![]() ),
х’1
),
х’1![]() +
х’2
+
х’2![]() ).
Но т.к.
).
Но т.к.
![]() и
и
![]() - собственные для А, то получаем ф(х1,х2)=(
(х’1 к1
- собственные для А, то получаем ф(х1,х2)=(
(х’1 к1![]() +
х’2 к2
+
х’2 к2![]() ),
х’1
),
х’1![]() +
х’2
+
х’2![]() )=
к1(х’1)2+ к2(х’2)2 . Получен новый вид
квадратичной формы, в котором отсутствует
произведение текущих координат. Такой
вид носит название – канонического
вида квадратичной формы.
)=
к1(х’1)2+ к2(х’2)2 . Получен новый вид
квадратичной формы, в котором отсутствует
произведение текущих координат. Такой
вид носит название – канонического
вида квадратичной формы.
Т.о. в декартовом базисе собственных нормированных векторов матрицы квадратичной формы сама форма принимает канонический вид.
Остается важная задача: установить
связь между координатами вектора
![]() =(
х1 х2)T начального базиса i,j и координатами
того же вектора
=(
х1 х2)T начального базиса i,j и координатами
того же вектора
![]() =(
х’1 х’2)T в новом базисе нормированных
собственных векторов матрицы квадратичной
формы.
=(
х’1 х’2)T в новом базисе нормированных
собственных векторов матрицы квадратичной
формы.
Мы имеем
![]() =
х1i+х2j = х’1I+х’2J . Но I и J тоже векторы,
правда единичной длины. И потому I=iCos
=
х1i+х2j = х’1I+х’2J . Но I и J тоже векторы,
правда единичной длины. И потому I=iCos![]() +jCos(90-
+jCos(90-![]() ),
J= iCos
),
J= iCos![]() +jCos(90+
+jCos(90+![]() ).
Или после подстановки полученного
вместо координат х’1,х’2 получим связь
между старыми и новыми координатами
).
Или после подстановки полученного
вместо координат х’1,х’2 получим связь
между старыми и новыми координатами
![]() =
=
![]() (
х’1 х’2)T, которая соответствует матрице
поворота плоскости на некоторый угол.
(
х’1 х’2)T, которая соответствует матрице
поворота плоскости на некоторый угол.