1.8.Линейное, евклидово и нормированное пространства.

Определение. Множество М элементов x,y,z…любой природы называютлинейным(аффинным, векторным)пространством,если выполнены требования:

1-е. Имеется правило, по которому любым двум элементам х и у из М ставится в соответствие третий элемент zиз М, называемый суммой и обозначаемыйx+y=z.

2-е. Имеется правило по которому любому элементу х из М и действительному числу к ставится в соответствие элемент у из М, называемый произведением числа на элемент и обозначаемый кx=y.

3-е. Указанные правила подчиняются законам (аксиомам):

1* - x+y=y+x: 2* - (x+y)+z=x+(y+z); 3* - существует элемент, называемый нуль элементом и обозначаемый 0, такой, чтоx+0=x; 4* - для каждого х существует элемент , называемый противоположный и обозначаемый -х, такой что х+(-х)=0; 5* 1х=х; 6* - с(кх)=(ск)х – сочетательный закон для умножения; 7* - (к+с)х=кх+сх – распределительный закон умножения относительно сложения; 8* - к(х+у)=кх+ку - распределительный закон сложения относительно умножения.

Если же природа элементов указана так же как и конкретный вид операций, то множество называют конкретным линейным пространством.

Примеры. Множество всех векторов на прямой (на плоскости, в пространстве) , если сложение определено по правилу треугольника (параллелограмма), а умножение на число как деформация, будет линейным векторным пространством с обозначением V₁(V₂,V₃).

Множество полиномов степени не выше 2 , если правила суммирования и умножения на число определены как обычно, линейное векторное пространство.

Множество функций, непрерывных на отрезке, множество решений однородной системы и т.д.

В то же время полиномов степени 2 , если правила суммирования и умножения на число определены как обычно, не будет линейным векторным пространством, т.к. возможно потеря старшей степени при суммировании таких полиномов (после приведения подобных).

Элементы линейных пространств принято называть векторами. А т.к. умножение производят на действительное число, то еще и действительными.

Опред. Выражение принято называть линейной комбинацией элементов (векторов) ЛП.

Опред. Элементы (векторы) {x_i} называют линейно независимыми , если их обращается в нуль тогда и только тогда, когда всеa_i=0.

Опред. Множество {x_i} ненулевых линейно независимых векторов (элементов) называют базисом ЛП, если для любого х не из этого множества существуют такие {a_i} не все равные нулю, что будет справедливо равенство х=. Последнее равенство называют разложением элемента х в базисе(по базису).

Опред. ЛП называют n-мерным, если в нем существуютnлинейно независимых вектора, аn+1 вектор уже будут линейно зависимыми.Nназывают размерность ЛП и записывают это такdimM=n.

Т.к. иных операций в ЛП не введено, то

Опред. Два ЛП называют изоморфными, если между их элементами установлено взаимно-однозначное соответствие ткк, что, если х и у принадлежат ЛП Mи им соответствуютx’ ,y’ из ЛПM’, то х+у соответствуетx’+y’, а кх соответствует кx’ из М’.

Из последнего следует, что единственной характеристикой ЛП является его размерность. Пишут так Mn.

Опред. Подмножество Lиз ЛП М, в котором справедливы указанные в определении ЛП операции называют линейным подпространством изMn.

Определение. Действительное ЛП называют евклидовым, если выполнены требования :

2. имеется правило, по которому любым х и у из ЛП ставится в соответствие действительное число, называемое скалярным произведением и обозначаемое (х,у);

3. указанное правило подчиняется аксиомам : а - (х,у)=(у,х); б – (х₁+х₂)у=х₁у+х₂у ; с – (кх,у)=к(х,у) для любого к ;d– (х,х)>0 , если х не нулевой и (х,х)=0, если х - нулевой.

Примерами евклидова пространства будут уже упоминаемые ранее V₁,V₂,V₃.

Примером ЕП будет множество упорядоченных совокупностей Аn, если операцию скалярное произведение определить по формуле (х,у)= .

Свойства. Для любых х и у из ЕП справедливо равенство (Коши-Буняковсого) (х,у)² (х,х)(у,у).

Доказательство. Согласно аксиомы dимеем (кх-у,кх-у)=к²(х,х)-2к(х,у)+(у,у)0. Для того , чтобы квадратный трехчлен был неотрицателен при любых значениях переменной к требуется , чтобы дискриминант был неположителен . Получаем (х,у)²-(х,х)(у,у) 0. Откуда и следует требуемое.

Опред. ЛП называют нормированным, если выполнены требования :

1. имеется правило, по которому любому х из ЛП ставится в соответствие действительное число, называемое нормой элемента и обозначаемое 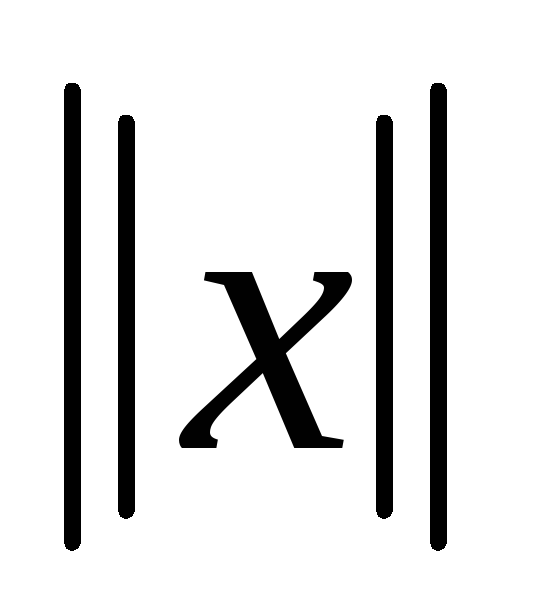(длиной);

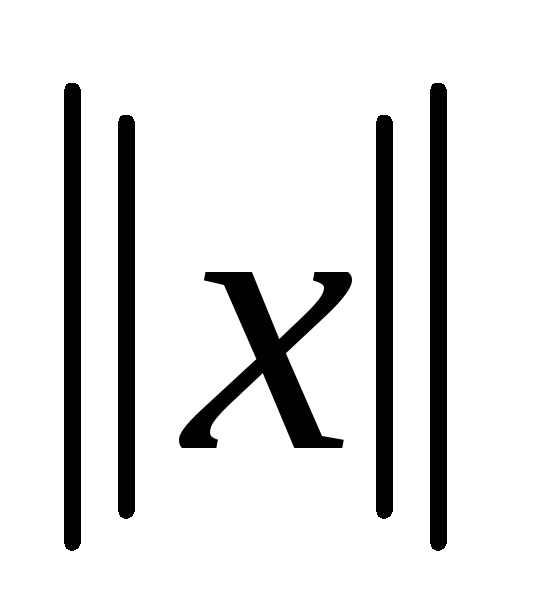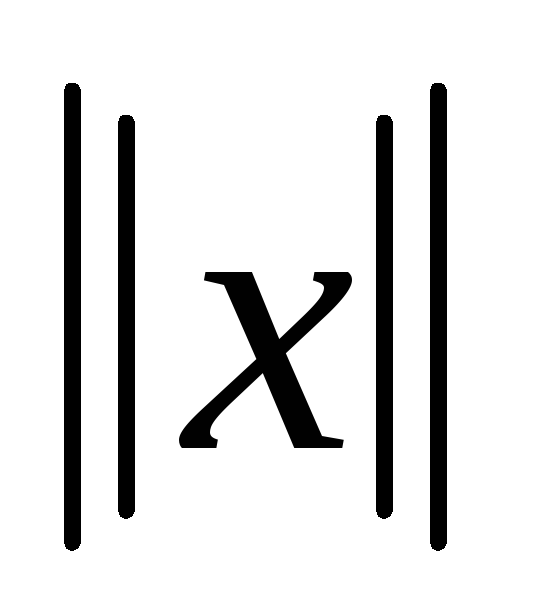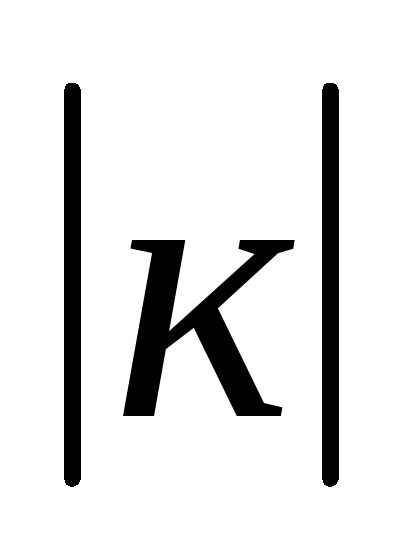
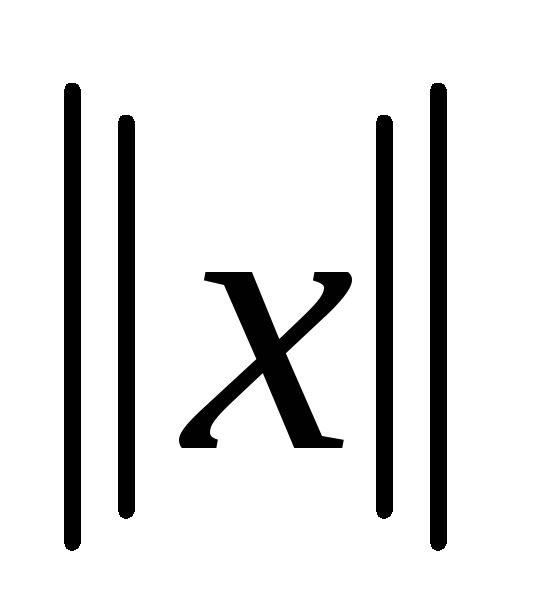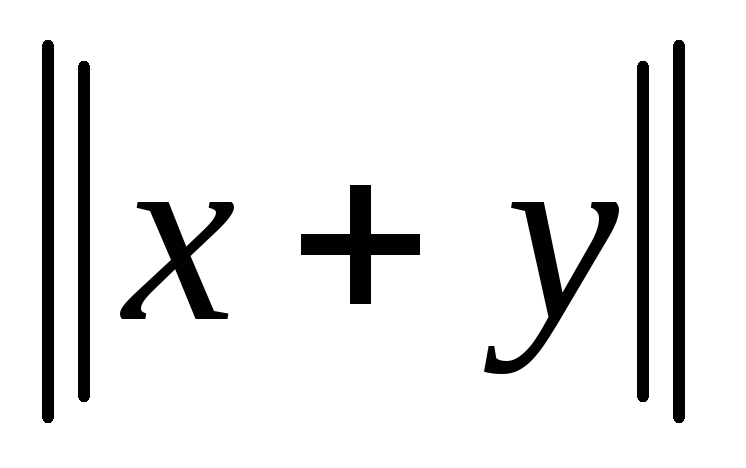
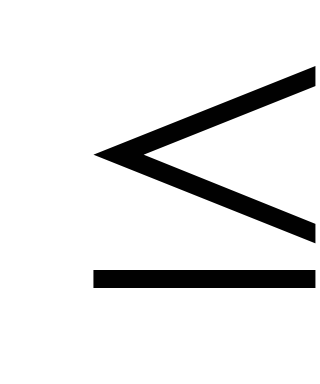
2. это правило подчиняется аксиомам : а - >0 , если х не нуль и =0, если х – нуль-элемент; б - =для любого действительного к; с – для любых х и у верно 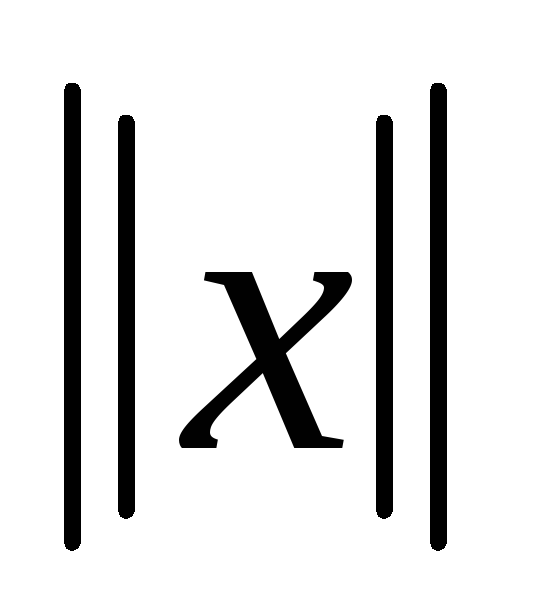+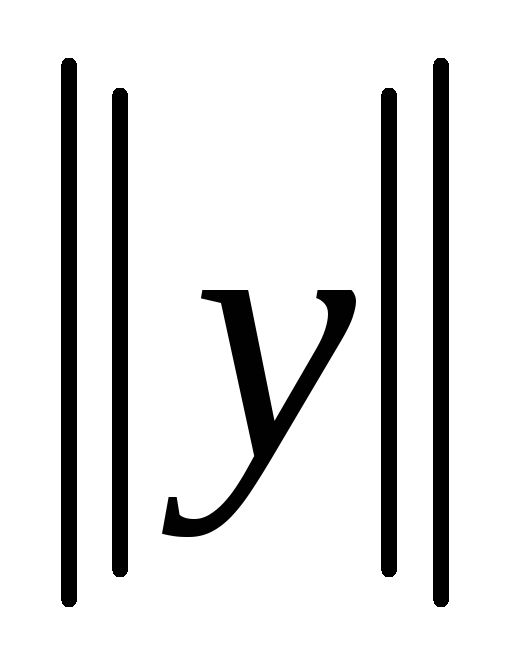- неравенство треугольника.

ЕП будет нормированным, если норму определить так =(корень квадратный из скалярного квадрата).

Опред. n– элементовe_i0 образуют ортонормированный базис в ЛП, если:

а – (e_i,e_i)= . Получение =1 называют нормированием.

Свойство. Если ЛП ортонормированно с базисом { e_i}, то (х,у)= .

Док-во. Пусть х и у произвольные из ЕП и { e_i} произвольный ортонормированный в нем. Тогда х=и у=. Но тогда (х,у)= (,)=, ввиду ортогональностиe_i.

Теперь легко выяснить смысл понятия ‘координата’ в ортонормированном базисе. Возьмем произвольный х=и произвольныйe_iиз базиса. Вычислим (х,e_i) =(,e_i)=x_i. Т.е. координата – это произведение вектора х на базисный орт.

в