
- •Белорусско-российский университет
- •1.2.Определители и их свойства
- •1.3.Системы линейных алгебраических уравнений
- •1.4.Формулы Крамера
- •1.5.Общий алгоритм решения системы линейных уравнений
- •1.6.Матричный метод решения линейной системы.
- •1.7.Понятие о приближенных методах решения линейных систем
- •1.8.Линейное, евклидово и нормированное пространства.
- •1.9.Линейные операторы и матрицы
- •1.10.Задача о собственных значениях
- •1.11.Свойства симметрических матриц
- •1.12.Квадратичные формы и их приведение к каноническому виду
- •Векторная алгебра
- •2.2.Скалярное произведение векторов
- •2.3.Векторное произведение векторов
- •2.4.Смешанное произведение векторов
- •2.5.Типовые задачи, решаемые средствами векторной алгебры
- •3.Аналитическая геометрия.
- •3.1.Уравнения линий и поверхностей
- •3.2.Уравнение 1-й степени на плоскости
- •3.3.Уравнения первой степени в пространстве
- •3.4.Уравнения первой степени в пространстве
- •3.5.Уравнения 2-й степени на плоскости
- •3.6.Уравнения 2-й степени в пространстве
- •3.7.Цилиндры и поверхности вращения
- •3.8.Упрощение кривых 2-го порядка
3.3.Уравнения первой степени в пространстве
Опред. Уравнением второго порядка в пространстве (уравнением поверхности 2-го порядка) называют уравнение вида
a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+a41x+a42y+a43z+ a44=0 (6.3)
Мы познакомимся только с уравнением (6.3), в котором отсутствуют произведения текущих координат. В этом случае имеется возможность выделить полные квадраты по переменным и получить уравнение поверхности в каноническом виде. Последние и будем изучать более подробно.
Для исследования канонических уравнений поверхностей второго порядка используют метод сечений. В самом простом виде он выглядит так: проводят серии плоскостей, параллельных координатным плоскостям и по результатам (виду сечений) делают вывод о форме поверхности. Эта работа похожа на работу томографа при исследовании внутренних органов человека в медлабораториях или работу топографа при топографической съемке местности.
Реализуем метод при построении
поверхности
![]() +
+![]() +
+![]() =1.Рассечем
поверхность плоскостямиz=h.
Тогда в сечении получим
=1.Рассечем
поверхность плоскостямиz=h.
Тогда в сечении получим
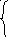
![]() +
+![]() =1-
=1-![]() , Из этой системы видно, чтоhне может превышать
, Из этой системы видно, чтоhне может превышать
z=h. с. Что означает – поверхность расположена между двумя
плоскостями – выше h=-cи нижеh=c. Более того, в сечениях получаются эллипсы, самый большой из которых расположен в плоскостиz=0. Чем дальше от плоскости хОу, тем меньше эллипс. И на высоте с эллипс вырождается в точку.
Если провести аналогичные серии плоскостей . параллельных другим координатным плоскостям, то получим похожие выводы. Следовательно, поверхность образована скольжением эллипсов по эллипса и называется трехосным эллипсоидом.
3.4.Уравнения первой степени в пространстве
Всякую плоскость в пространстве геометрически однозначно задать:
-точкой Мо(хо;уо,zо;)
на плоскости и вектором
![]() (А;В;С)
нормальным к ней;
(А;В;С)
нормальным к ней;
-точкой Мо(хо;уо,zо;) и расстояниемdот начала координат до плоскости;
-тремя точками на плоскости;
-двумя точками на плоскости и вектором, параллельным ей и т.д.
Во всех случаях – это задачи 2-го типа
и решаются они по одной схеме. Пусть
плоскость задана точкой Мо(хо;уо,zо;) и вектором
![]() (А;В;С)
нормальным к ней. Тогда возьмем на
плоскости точку М(х;у;z).
И тогда векторы М Мо и
(А;В;С)
нормальным к ней. Тогда возьмем на
плоскости точку М(х;у;z).
И тогда векторы М Мо и
![]() будут ортогональны и получим А(х- хо)+В(у-
уо)+С(z-zо)=0
–уравнение плоскости, проходящей
через заданную точку перпендикулярно
вектору. Если раскрыть скобки и
привести подобные, то получимобщее
уравнение плоскостиАх+Ву+Сz+D=0.
Из этого уравнения видно, что всякое
уравнение первой степени с тремя
переменными – уравнение плоскости в
пространстве. Можно рассматривать
частные его случаи в зависимости от
значений коэффициентов А,В,С,D.
будут ортогональны и получим А(х- хо)+В(у-
уо)+С(z-zо)=0
–уравнение плоскости, проходящей
через заданную точку перпендикулярно
вектору. Если раскрыть скобки и
привести подобные, то получимобщее
уравнение плоскостиАх+Ву+Сz+D=0.
Из этого уравнения видно, что всякое
уравнение первой степени с тремя
переменными – уравнение плоскости в
пространстве. Можно рассматривать
частные его случаи в зависимости от
значений коэффициентов А,В,С,D.
Типовые задачи на плоскость в пространстве.
1.Разные виды уравнений и переходы от одного к другому виду.
2.Расстояние от точки до плоскости.
3.Угол между плоскостями (и взаимное расположение плоскостей).
4.Точка пересечения плоскостей.
5.Пучок плоскостей и др. более сложные задачи.
Комментарий. Следует запомнить жестко наиболее простую для аналитической геометрии ситуацию : для поиска уравнения плоскости следует указать точку, через которую полоскость проходит, и вектор, нормальный плоскости.
Прямую линию в пространстве в аналитической геометрии задают в виде
пересечения двух плоскостей
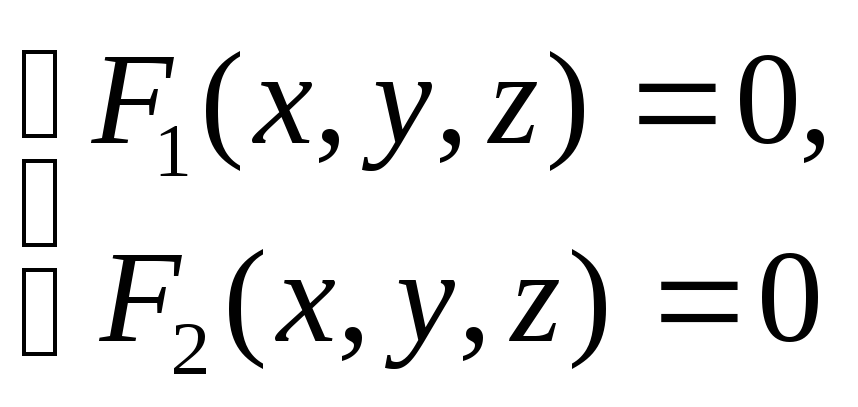 или
или
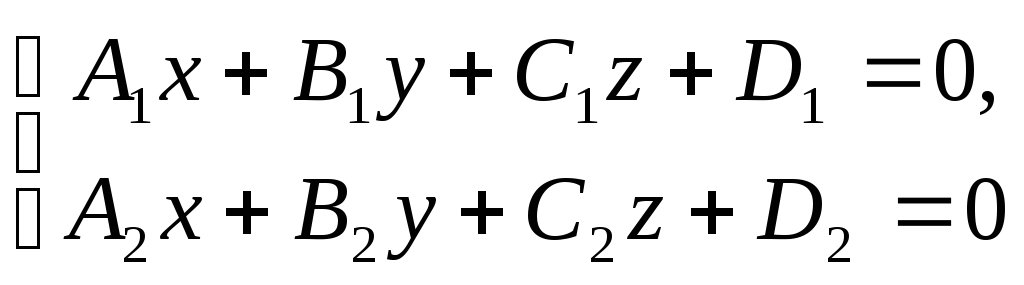 .
.
Можно того же результата добиться, задав
прямую проходящей через две заданные
точки Мо(хо;уо,zо)
и М1(х1;у1;z1).
Тогда из условий параллельности(коллинеарности)
векторов ММо и МоМ1получим![]() . Если же обозначить вектор МоМ1=
. Если же обозначить вектор МоМ1=
![]() (m;n;p),
то получим канонические уравнения
прямой в пространстве
(m;n;p),
то получим канонические уравнения
прямой в пространстве ![]() .
В последних двух способах задания
прямой в пространстве “потеряны”
уравнения двух плоскостей. Комментарием
к этому может служить такое указание –
мы имеем равенство трех отношений. Так
что , фактически, мы имеет даже три
плоскости вместо двух (если сравнивать
по два разных отношения, то всегда
получится уравнение первого порядка в
пространстве – уравнение плоскости).
Особенностями этих плоскостей будет
следующее – каждая из них является
проектирующей данную прямую на некоторую
координатную плоскость (в каждом
уравнении плоскости только две переменные
– значит плоскость перпендикулярна
координатной плоскости).
.
В последних двух способах задания
прямой в пространстве “потеряны”
уравнения двух плоскостей. Комментарием
к этому может служить такое указание –
мы имеем равенство трех отношений. Так
что , фактически, мы имеет даже три
плоскости вместо двух (если сравнивать
по два разных отношения, то всегда
получится уравнение первого порядка в
пространстве – уравнение плоскости).
Особенностями этих плоскостей будет
следующее – каждая из них является
проектирующей данную прямую на некоторую
координатную плоскость (в каждом
уравнении плоскости только две переменные
– значит плоскость перпендикулярна
координатной плоскости).
Важно уметь делать переход от одного вида уравнения к другому и понимать смысл этих математических действий в геометрии.
П ример
6.2. Найти, если таковая имеется, точку
пересечения трех плоскостей 2х+2у+z=19,
ример
6.2. Найти, если таковая имеется, точку
пересечения трех плоскостей 2х+2у+z=19,
x+2y+4z=31, Решение.Сразу видно, что ранг основной и расширен-
4x+6y+9z=-2.
ной матриц не болше
3 и не меньше 2. Для уточнения вычислим
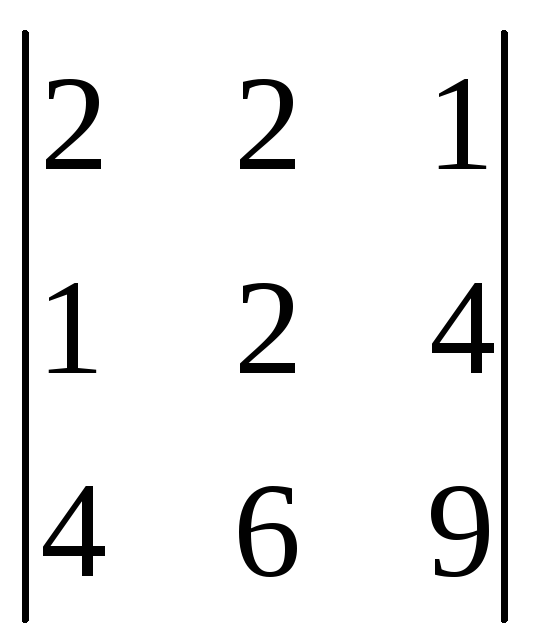 =
=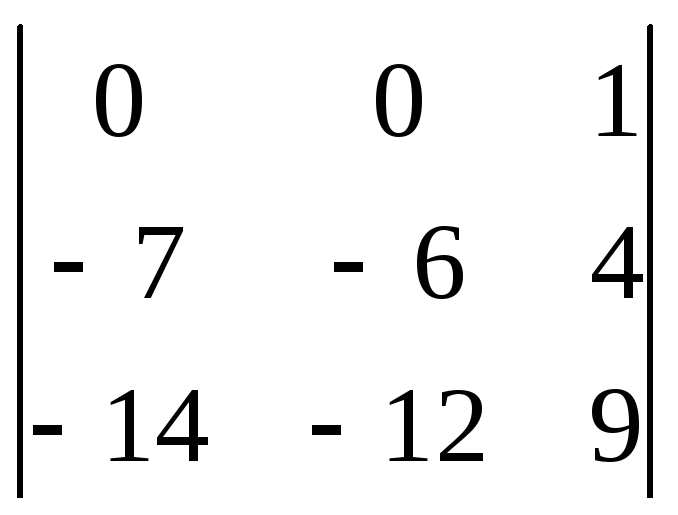 =0.
Т.о.rancA=2. Для расширенной
матрицы имеем
=0.
Т.о.rancA=2. Для расширенной
матрицы имеем
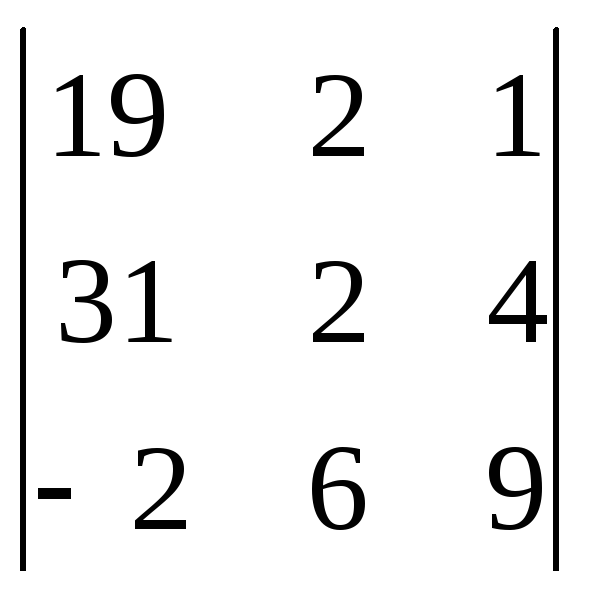 =
=
![]() 0.
Т.е.rancA’=3. Система
противоречива – точки пересечения нет.
Геометрически это говорит в данном
случае о такой ситуации: параллельных
плоскостей нет; следовательно плоскости
попарно пересекаются и образуют подобие
треугольной призмы.
0.
Т.е.rancA’=3. Система
противоречива – точки пересечения нет.
Геометрически это говорит в данном
случае о такой ситуации: параллельных
плоскостей нет; следовательно плоскости
попарно пересекаются и образуют подобие
треугольной призмы.
При взаимном расположении прямой и
плоскости следует учитывать, что:
полскость характеризуется норамлью
![]() и
точкой Мо(хо;уо,zо)
на плоскости, а прямая – направляющим
вектором
и
точкой Мо(хо;уо,zо)
на плоскости, а прямая – направляющим
вектором
![]() (m;n;p)
и точкой М1(х1;у1;z1)
на прямой .
(m;n;p)
и точкой М1(х1;у1;z1)
на прямой .
Так, если плоскость параллельна прямой
, то имеем всегда
![]()
![]() =0,
а если плоскость перпендикулярна
прямой,то всегда
=0,
а если плоскость перпендикулярна
прямой,то всегда
![]() коллинеарен
коллинеарен![]() . Если требуется найти точку пересечения
прямой и плоскости, то систему
. Если требуется найти точку пересечения
прямой и плоскости, то систему
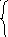 Ах+Ву+Сz+D=0
Ах+Ву+Сz+D=0
![]() можно (и даже лучше) решать так: последнее
отношение приравнять параметруt;
затем выразить через параметр переменныеx,y,z(x=mt+ хо,e=nt+yо,z=pt+zо;
затем найденное подставить в уравнение
плоскости и найти значение параметраtдля точки пересечения;
после этого вычислить координаты точки
пересечения через значение параметра.
можно (и даже лучше) решать так: последнее
отношение приравнять параметруt;
затем выразить через параметр переменныеx,y,z(x=mt+ хо,e=nt+yо,z=pt+zо;
затем найденное подставить в уравнение
плоскости и найти значение параметраtдля точки пересечения;
после этого вычислить координаты точки
пересечения через значение параметра.
