
- •Белорусско-российский университет
- •1.2.Определители и их свойства
- •1.3.Системы линейных алгебраических уравнений
- •1.4.Формулы Крамера
- •1.5.Общий алгоритм решения системы линейных уравнений
- •1.6.Матричный метод решения линейной системы.
- •1.7.Понятие о приближенных методах решения линейных систем
- •1.8.Линейное, евклидово и нормированное пространства.
- •1.9.Линейные операторы и матрицы
- •1.10.Задача о собственных значениях
- •1.11.Свойства симметрических матриц
- •1.12.Квадратичные формы и их приведение к каноническому виду
- •Векторная алгебра
- •2.2.Скалярное произведение векторов
- •2.3.Векторное произведение векторов
- •2.4.Смешанное произведение векторов
- •2.5.Типовые задачи, решаемые средствами векторной алгебры
- •3.Аналитическая геометрия.
- •3.1.Уравнения линий и поверхностей
- •3.2.Уравнение 1-й степени на плоскости
- •3.3.Уравнения первой степени в пространстве
- •3.4.Уравнения первой степени в пространстве
- •3.5.Уравнения 2-й степени на плоскости
- •3.6.Уравнения 2-й степени в пространстве
- •3.7.Цилиндры и поверхности вращения
- •3.8.Упрощение кривых 2-го порядка
2.4.Смешанное произведение векторов
Рассмотрим произведения трех векторов :
((![]() ,
,![]() ),
),![]() )
– уже известное нам произведение скаляра
на вектор – и потому ничего нового;
)
– уже известное нам произведение скаляра
на вектор – и потому ничего нового;
[[![]() ,
,![]() ],
],![]() ]
- двойное векторное произведение,
которое имеет узкое приложение в
механике;
]
- двойное векторное произведение,
которое имеет узкое приложение в
механике;
([![]() ,
,![]() ],
],![]() )
– векторно-скалярное (смешанное)
произведение, которое имеет широкое
применение в математике и приложениях.
)
– векторно-скалярное (смешанное)
произведение, которое имеет широкое
применение в математике и приложениях.
Анализируя известное произведение [![]() ,
,![]() ]
по Рис.2.2, можно получить геометрическую
интерпретацию для смешанного произведения
]
по Рис.2.2, можно получить геометрическую
интерпретацию для смешанного произведения
([![]() ,
,![]() ],
],![]() ).
Модуль векторного произведения –
площадь параллелограмма, построенного
на векторах-множителях и равной
).
Модуль векторного произведения –
площадь параллелограмма, построенного
на векторах-множителях и равной![]() =
=![]() .
Если теперь перемножить скалярно векторы
.
Если теперь перемножить скалярно векторы![]() и
и![]() ,
то получим отрезок ОВ, равный высоте
параллелепипеда, построенного на
векторах-сомножителях
,
то получим отрезок ОВ, равный высоте
параллелепипеда, построенного на
векторах-сомножителях![]() ,
,![]() ,
,![]() как на ребрах. Т.о., модуль ([
как на ребрах. Т.о., модуль ([![]() ,
,![]() ],
],![]() )
численно равен объему параллелепипеда,
построенного на векторах множителях.
)
численно равен объему параллелепипеда,
построенного на векторах множителях.
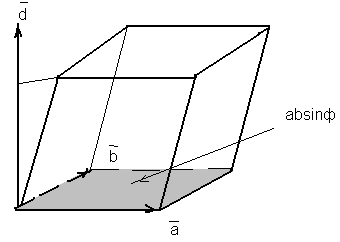
К определению ([![]() ,
,![]() ],
],![]() )
)
Используя координатную форму векторного произведения, получаем координатную форму смешанного произведения
([![]() ,
,![]() ],
],![]() )=
)=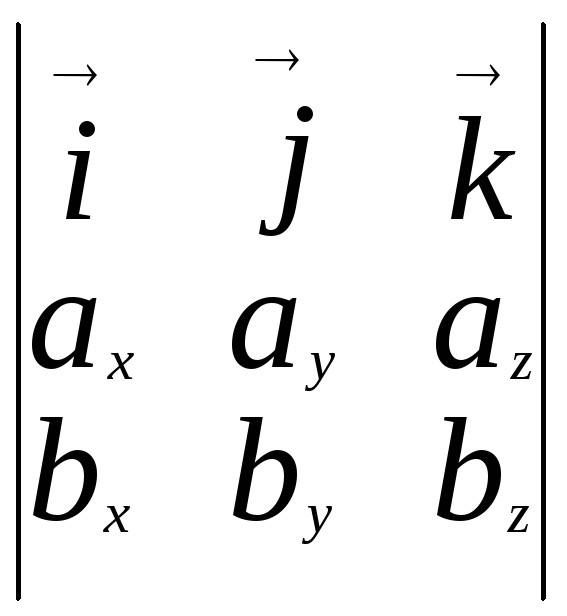 ( сx
( сx![]() +сy
+сy![]() +сz
+сz![]() )=((aхbу-aybx)
)=((aхbу-aybx)![]() +(azbx-axbz)
+(azbx-axbz)![]() +(aybz-azbу)
+(aybz-azbу)![]() )
) ( сx
)
) ( сx![]() +сy
+сy![]() +сz
+сz![]() )=(aхbу-aybx) сx+(azbx-axbz)
сy+(aybz-azbу)
сz= =
)=(aхbу-aybx) сx+(azbx-axbz)
сy+(aybz-azbу)
сz= =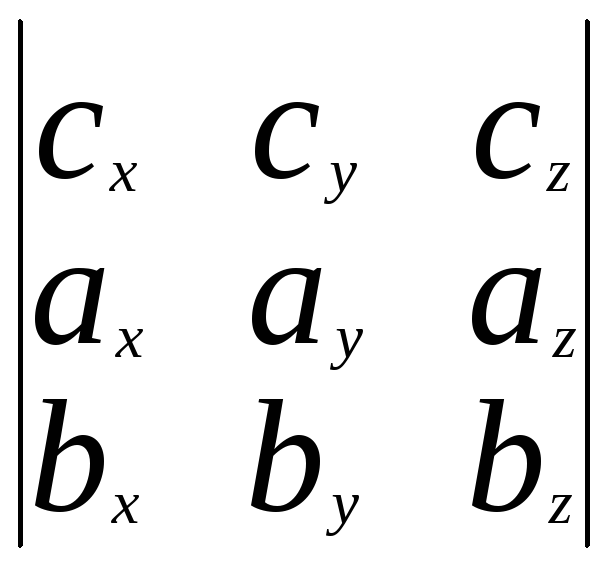 .
Если в последнем определителе переставим
местами 1-ю и 3-ю строки, то определитель
не изменится и мы получим более удобную
запись координат перемножаемых векторов
в порядке их следования в произведении.
.
Если в последнем определителе переставим
местами 1-ю и 3-ю строки, то определитель
не изменится и мы получим более удобную
запись координат перемножаемых векторов
в порядке их следования в произведении.
Из последней формулы для вычисления
смешанного произведения следует
возможность проверки компланарности
(параллельности одной плоскости) трех
векторов – если ([![]() ,
,![]() ],
],![]() )=0,
то векторы-множители компланарны. И
следствием последнего равенства будет
условие линейной зависимости трех
векторов в пространстве .
)=0,
то векторы-множители компланарны. И
следствием последнего равенства будет
условие линейной зависимости трех
векторов в пространстве .
2.5.Типовые задачи, решаемые средствами векторной алгебры
Деление отрезка в данном отношении k.
Определение. Пусть дан отрезок АВ и
точка М на нем или его продолжении.
Говорят, сто М делит АВ в отношении к,
если k=![]() АМ/MB.
При этом знак + берут, если векторы
АМ/MB.
При этом знак + берут, если векторы![]() и
и![]() сонаправлены и знак --, если противоположно
направлены.
сонаправлены и знак --, если противоположно
направлены.
Решение задачи. Из определения следует
соотношение
![]() =к
=к![]() .
Но точно таким же соотношением связаны
соответствующие координаты указанных
векторов. Получаем
.
Но точно таким же соотношением связаны
соответствующие координаты указанных
векторов. Получаем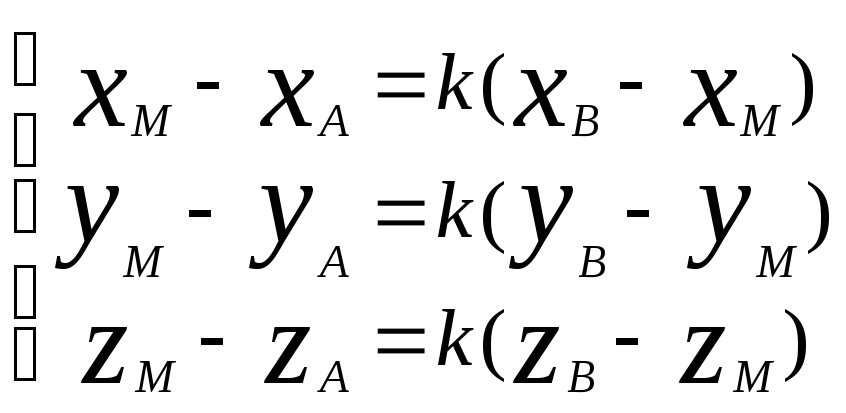 из которой следуют формулы для вычисления
координатделящей точкихМ =
из которой следуют формулы для вычисления
координатделящей точкихМ =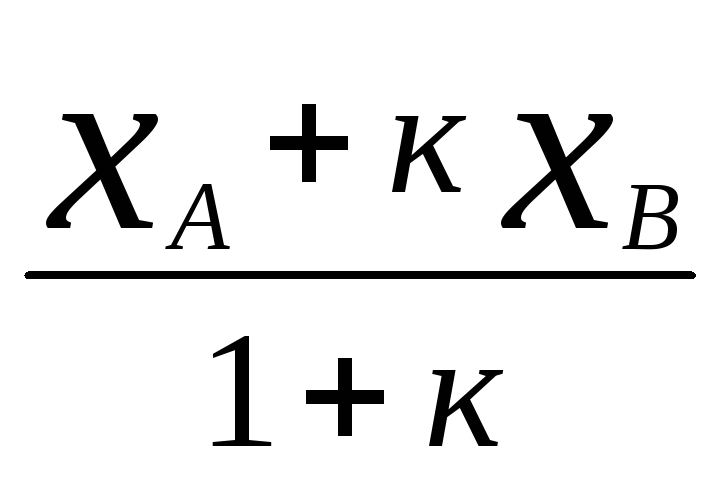 и т.д.
и т.д.
Получение единичного вектораданного
направления![]() .
Дан вектор
.
Дан вектор![]() (ах, ау,az)
– своими координатами. Найти вектор
единичной длины и того же направления.
(ах, ау,az)
– своими координатами. Найти вектор
единичной длины и того же направления.
Решение. Интересующий нас вектор равен
![]() =
=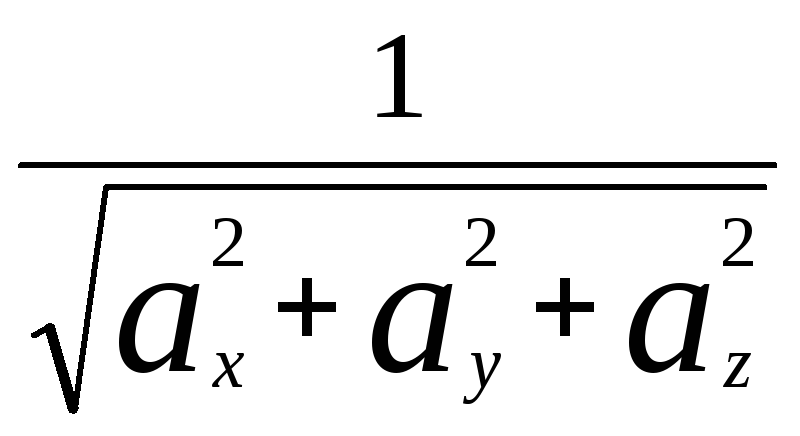 (ax
(ax![]() +ay
+ay![]() +az
+az![]() )=
)=![]() Cos
Cos![]() +
+![]() Cos
Cos![]() +
+![]() Cos
Cos![]() .
.
Угол между векторамиCosф=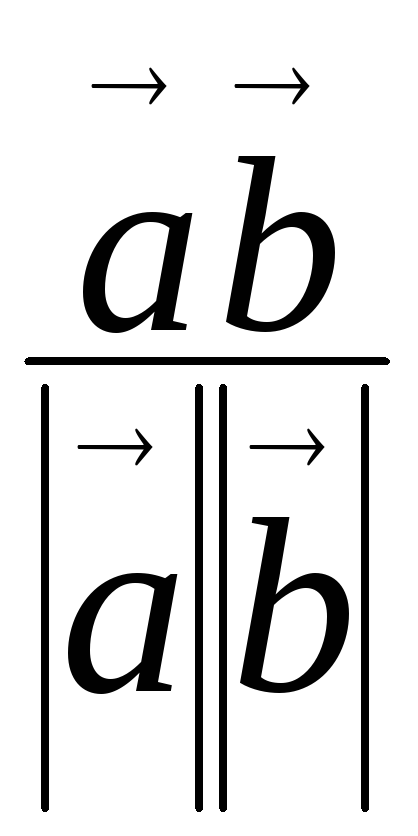 .
.
Проверка параллельности и перпендикулярности векторов.
Вычисление площадей многоугольников,
разбиением их на треугольники и используя
равенство из геометрической интерпретации
векторного произведения. Имеем
![]() =0,5
=0,5
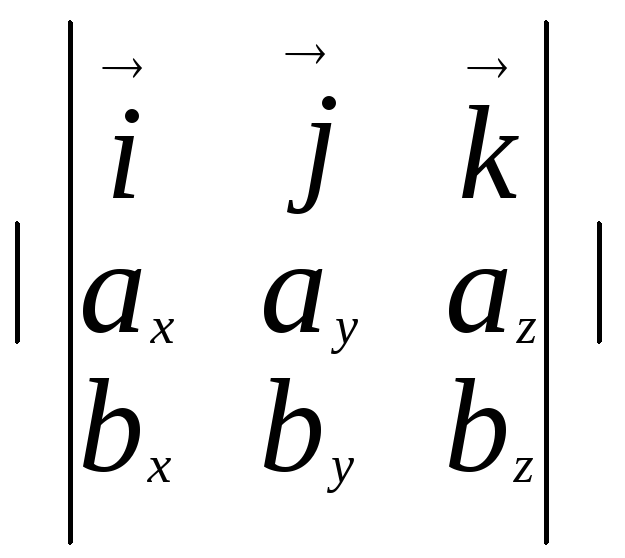 .
.
Расстояние от точки Мо(хо;уо)
до прямойс вектором![]() .
.
d=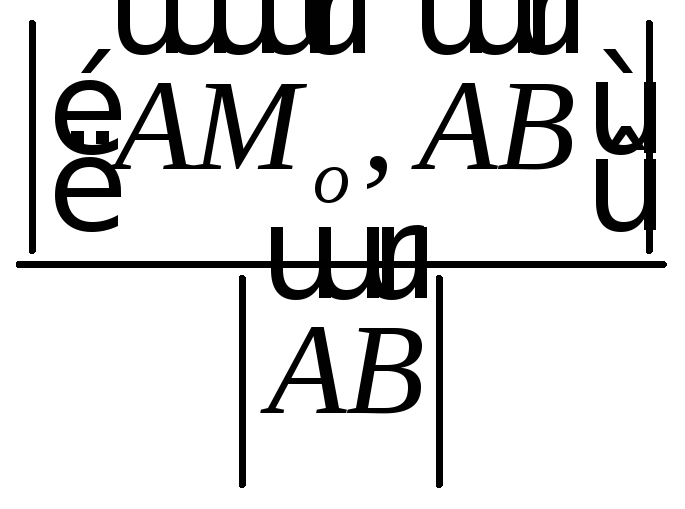 .Используя
рисунок, видно, что числитель – это
площадь,
.Используя
рисунок, видно, что числитель – это
площадь,
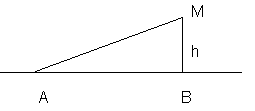
а знаменатель – это основание
параллелограмма со сторонами
![]() и
и![]() .
.
3.Аналитическая геометрия.
Отличительной особенностью разделов аналитической геометрии является принцип манипулирования с формулами , истолковывая действия как геометрические преобразования некоторых геометрических объектов. Важно усвоить этот принцип и тогда решение задач принимает простой и интересный процесс.
