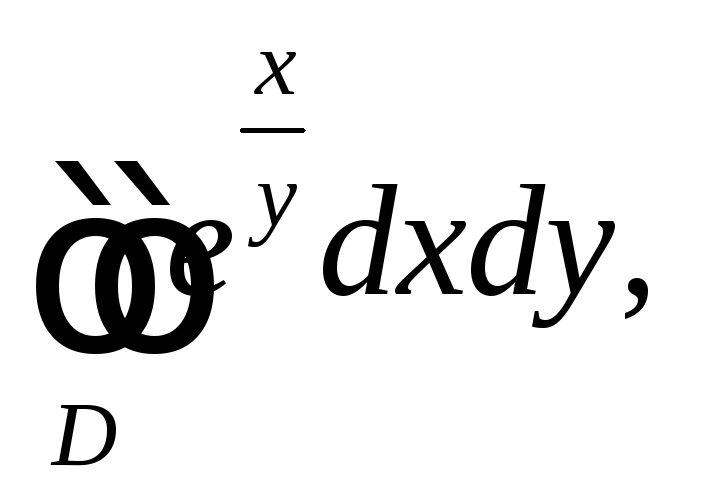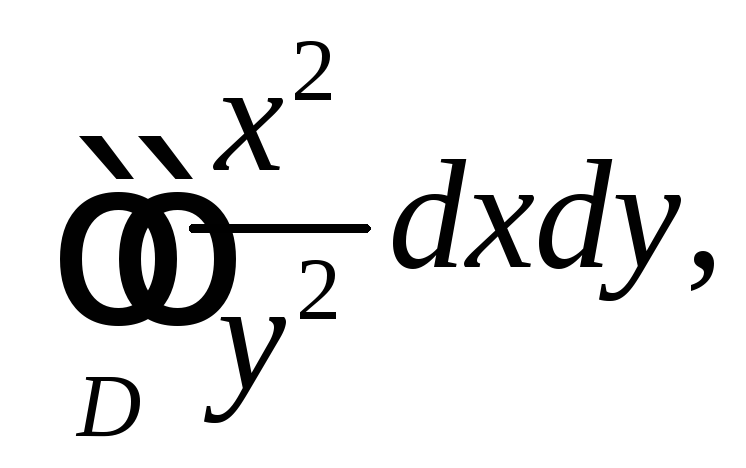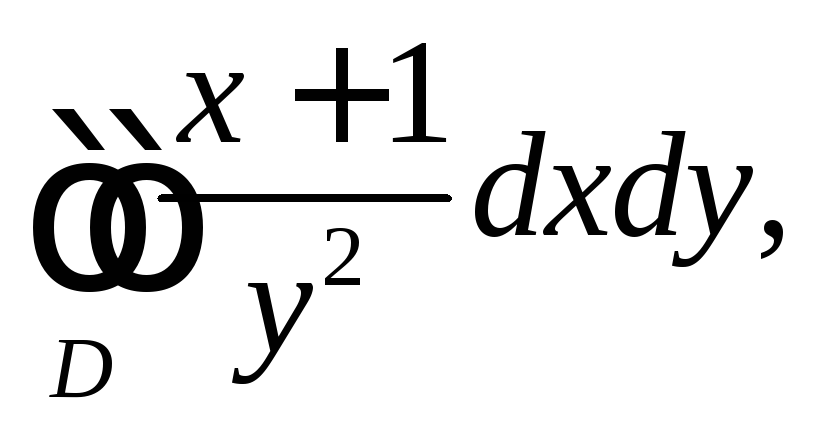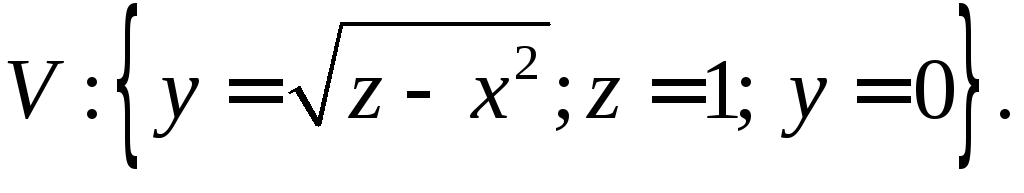- •212005, Г. Могилев, пр. Мира, 43
- •Содержание
- •1 Программа курса
- •Тема 1. Интегральное исчисление функций одной переменной.
- •Тема 2. Дифференциальное и интегральное исчисление функций многих переменных.
- •2 Общие требования к оформлению контрольной работы
- •2.1 Выбор варианта задания
- •2.2 Правила оформления контрольной работы
- •3 Решение типового варианта
- •4. Варианты контрольных заданий
- •Приложение
- •Список литературы
- •4. Варианты контрольных заданий
4. Варианты контрольных заданий
Задание 1. Найти следующие интегралы:
|
1.1 |
а)
|
б)
|
|
1.2 |
а)
|
б)
|
|
1.3 |
а)
|
б)
|
|
1.4 |
а)
|
б)
|
|
1.5 |
а)
|
б)
|
|
1.6 |
а)
|
б)
|
|
1.7 |
а)
|
б)
|
|
1.8 |
а)
|
б)
|
|
1.9 |
а)
|
б)
|
|
1.10 |
а)
|
б)
|
|
1.11 |
а)
|
б)
|
|
1.12 |
а)
|
б)
|
|
1.13 |
а)
|
б)
|
|
1.14 |
а)
|
б)
|
|
1.15 |
а)
|
б)
|
|
1.16 |
а)
|
б)
|
|
1.17 |
а)
|
б)
|
|
1.18 |
а)
|
б)
|
|
1.19 |
а)
|
б)
|
|
1.20 |
а)
|
б)
|
|
1.21 |
а)
|
б)
|
|
1.22 |
а)
|
б)
|
|
1.23 |
а)
|
б)
|
|
1.24 |
а)
|
б)
|
|
1.25 |
а) |
б)
|
|
1.26 |
а)
|
б)
|
|
1.27 |
а)
|
б)
|
|
1.28 |
а)
|
б)
|
|
1.29 |
а)
|
б)
|
|
1.30 |
а)
|
б)
|
Задание 2 . Вычислить определенный интеграл.
2.1
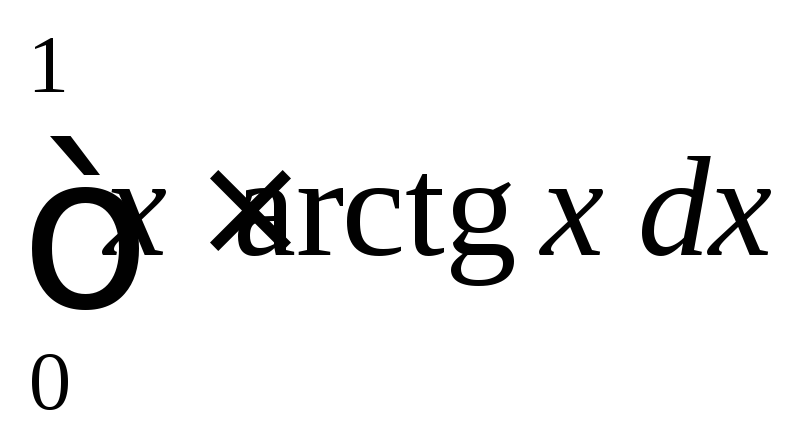 .
.
2.2
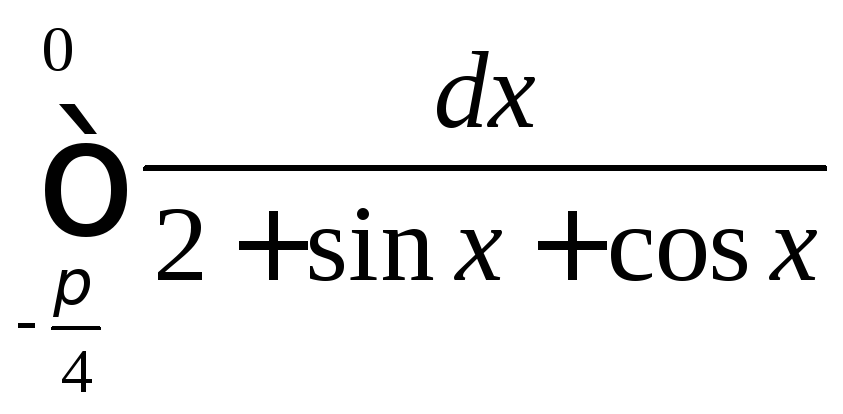 .
.
2.3
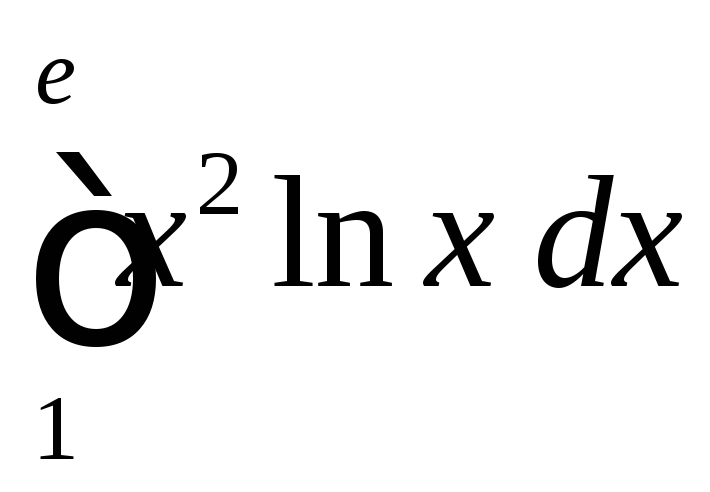 .
.
2.4
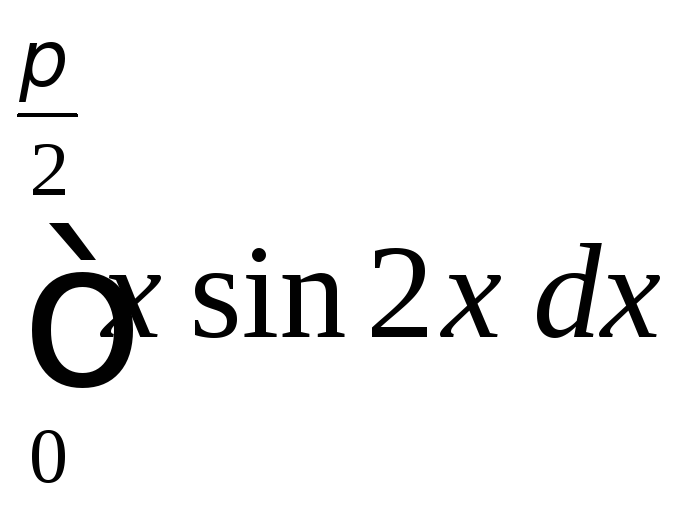 .
.
2.5
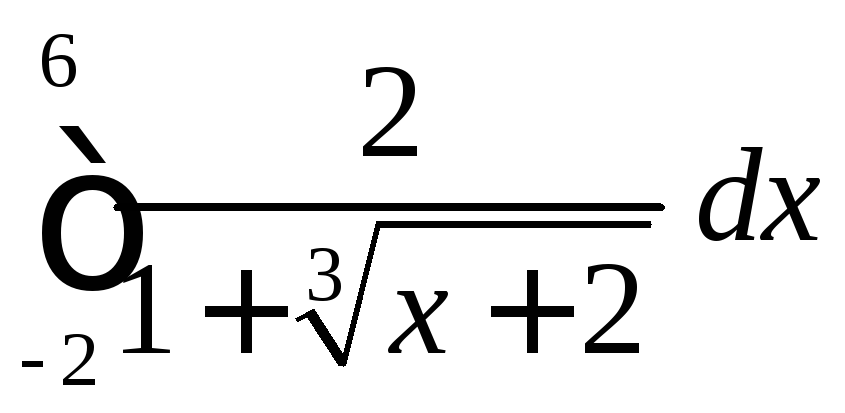 .
.
2.6
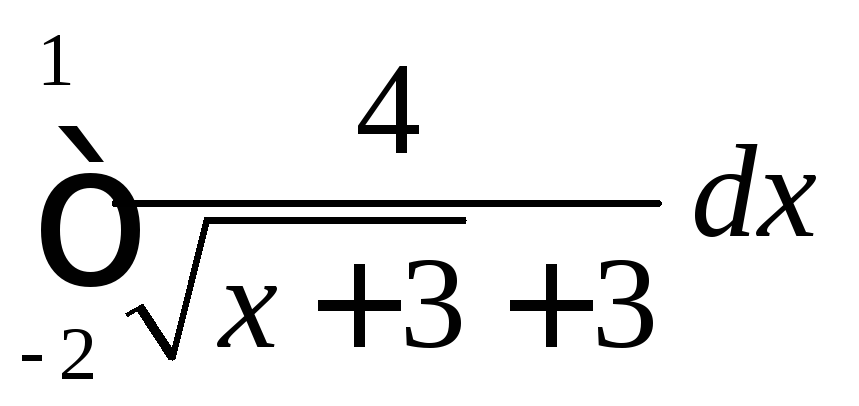 .
.
2.7
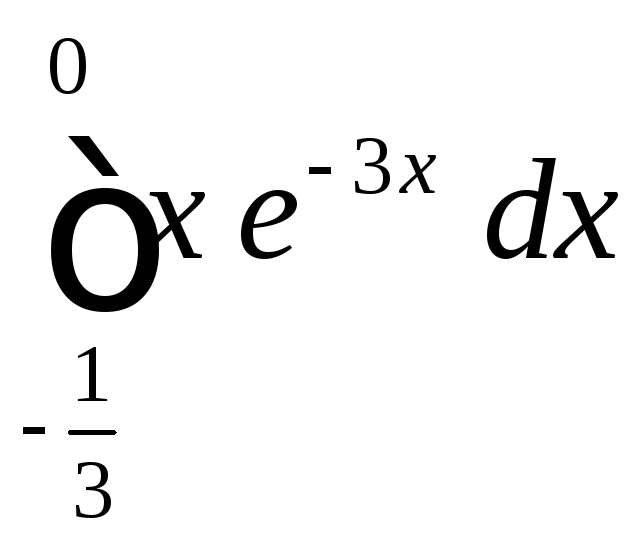 .
.
2.8
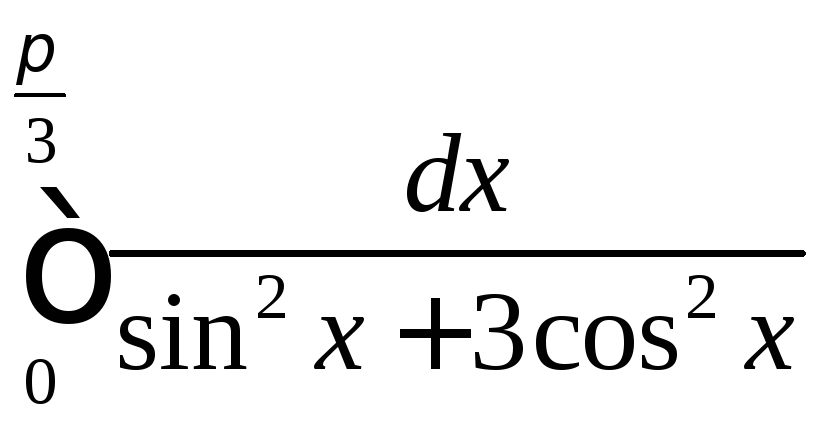 .
.
2.9
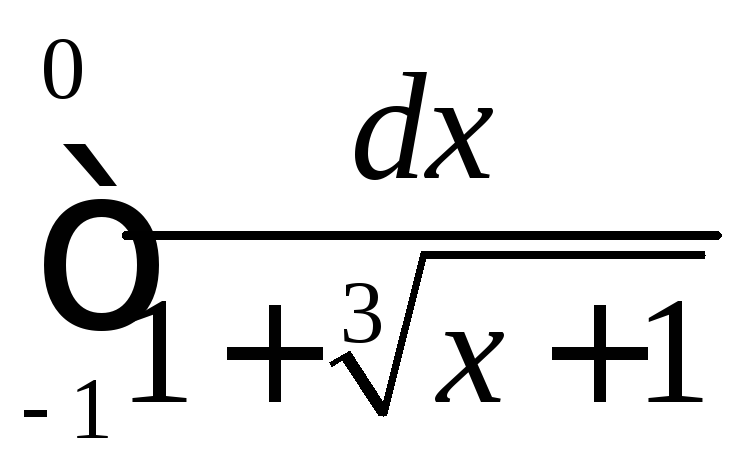 .
.
2.10
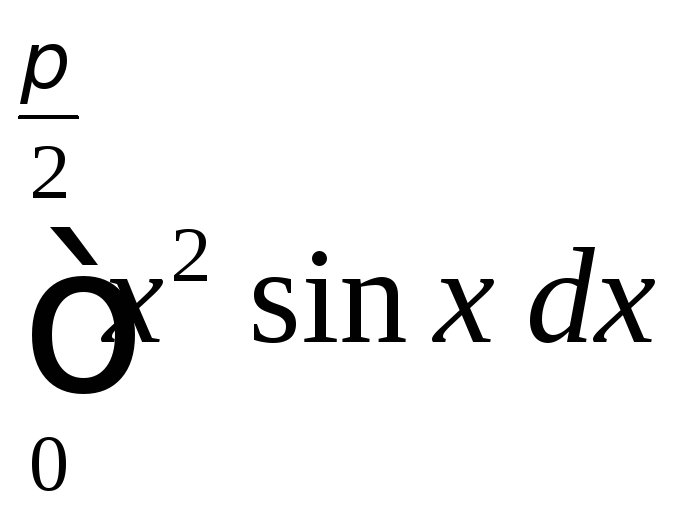 .
.
2.11
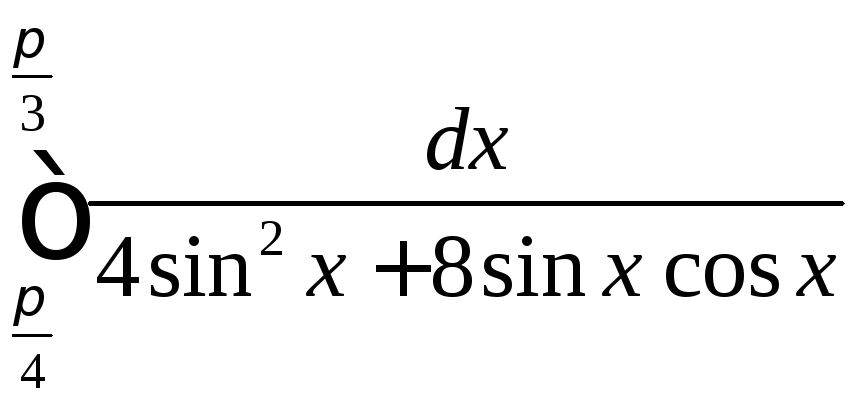 .
.
2.12
 .
.
2.13
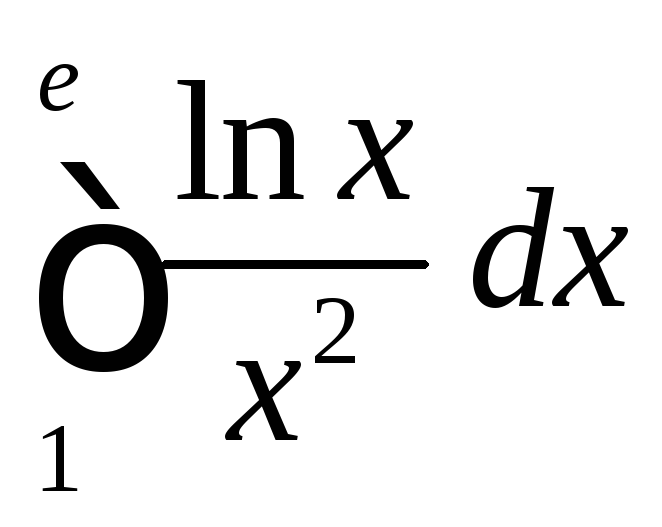 .
.
2.14
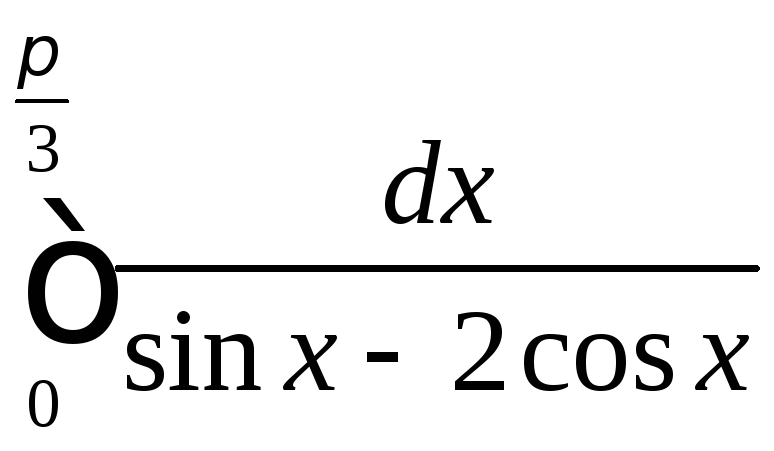 .
.
2.15
 .
.
2.16
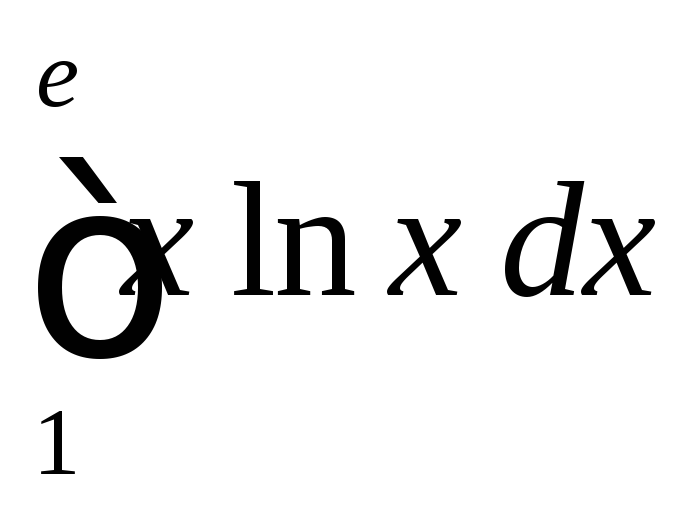 .
.
2.17
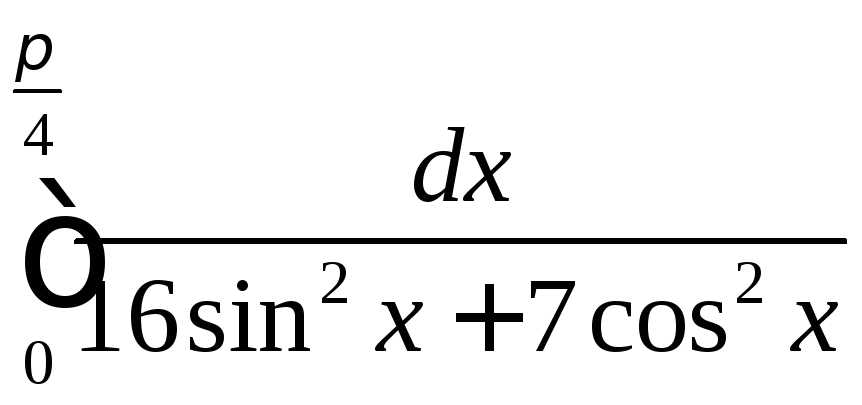 .
.
2.18
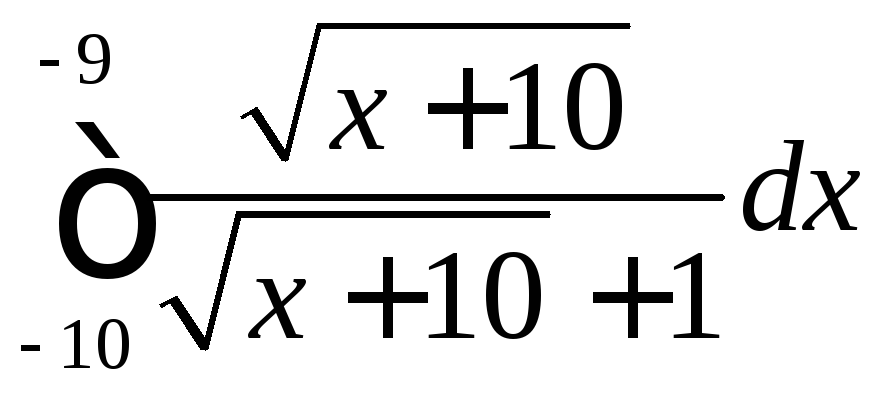
2.19
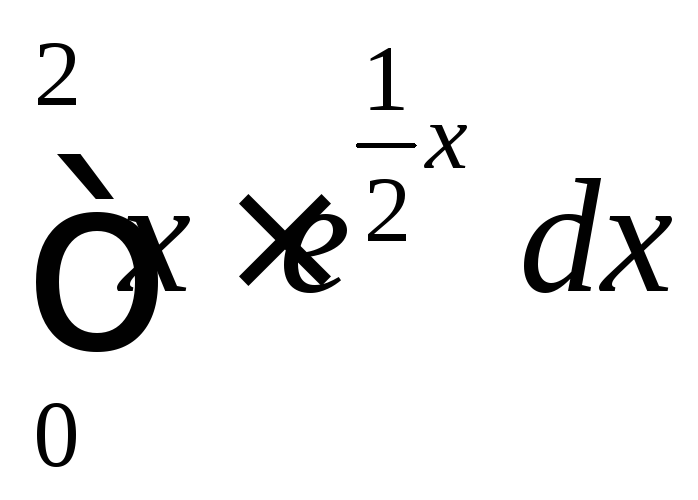
2.20
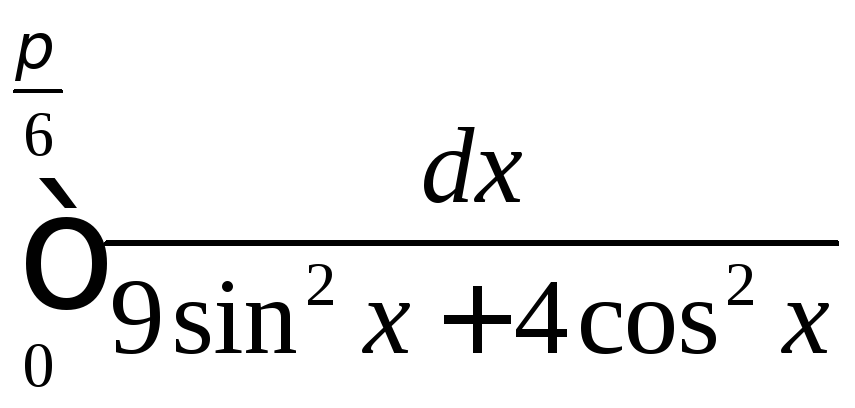 .
.
2.21
 .
.
2.22
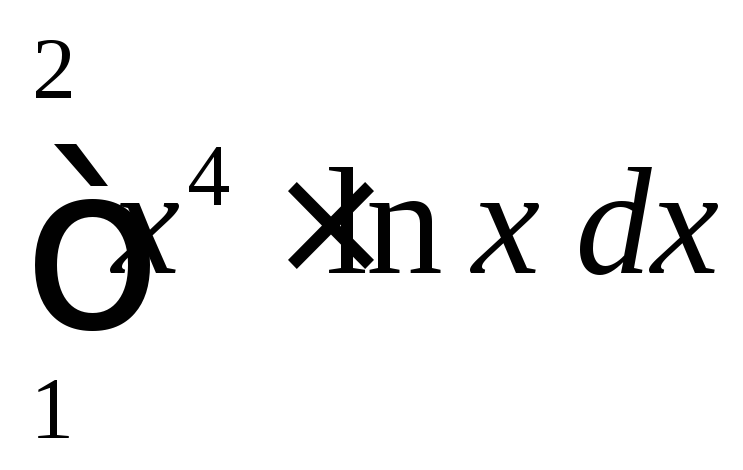 .
.
2.23
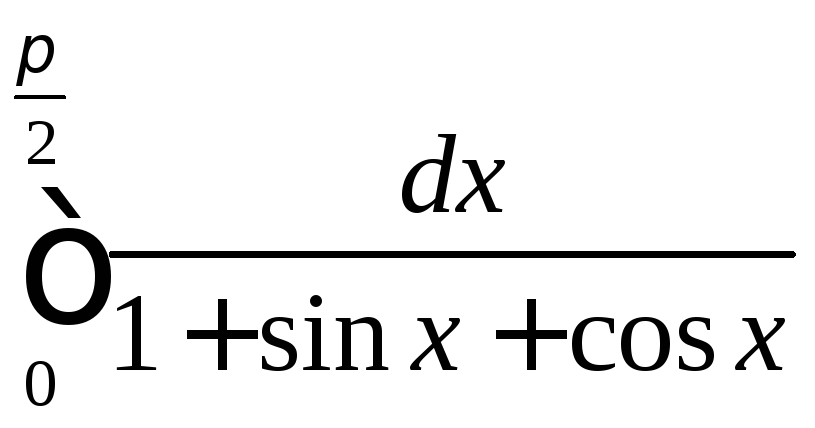 .
.
2.24
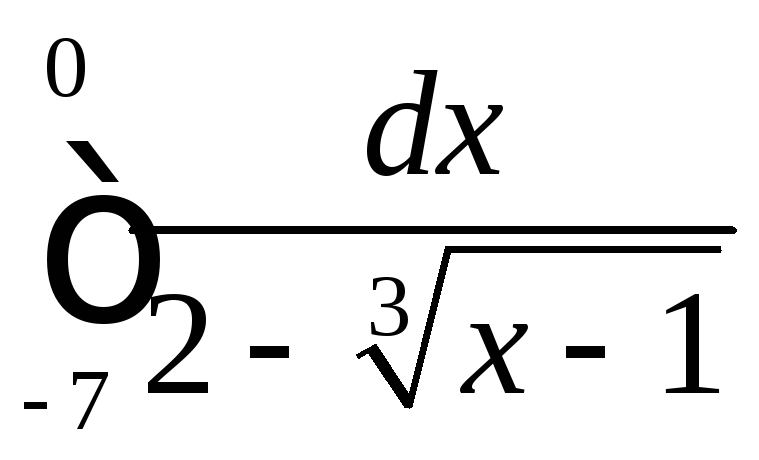 .
.
2.25
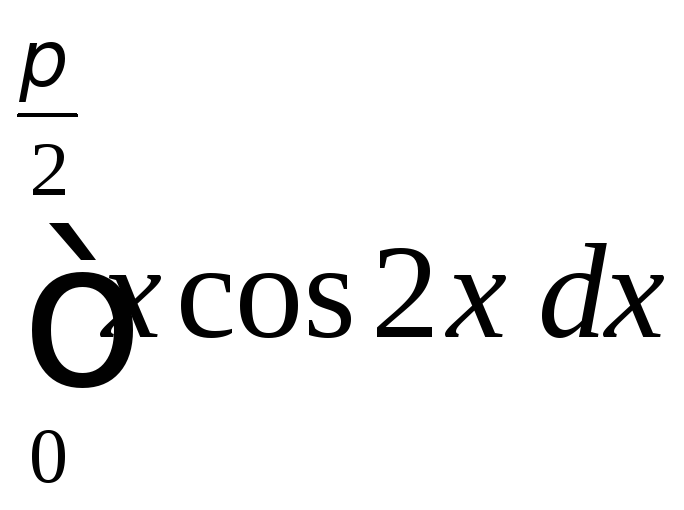 .
.
2.26
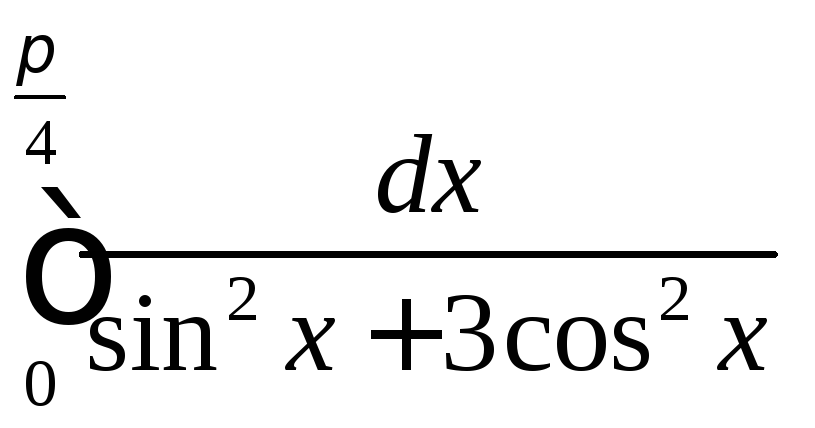 .
.
2.27
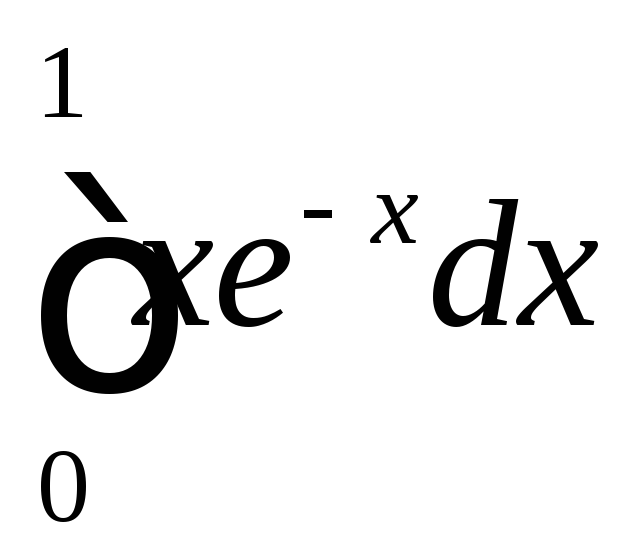 .
.
2.28
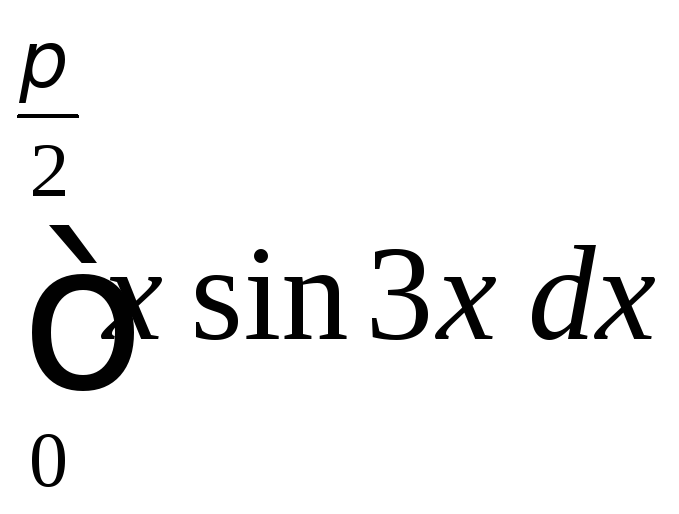 .
.
2.29
 .
.
2.30
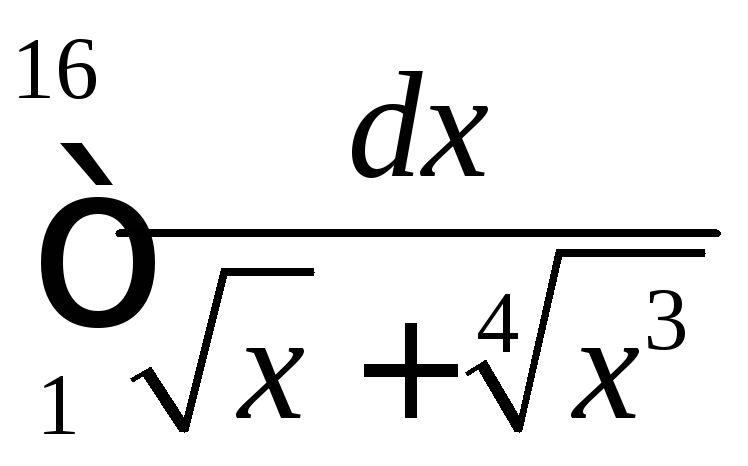 .
.
Задание 3. Вычислить площадь фигуры, ограниченной линиями.
3.1
![]() ,
,![]() .
.
3.2
![]() ,
,![]() .
.
3.3
![]() ,
,![]() .
.
3.4
![]() ,
,![]() .
.
3.5
![]() ,
,![]() .
.
3.6
![]() ,
,![]() .
.
3.7
![]() ,
,![]() .
.
3.8
![]() ,
,![]() .
.
3.9
![]() ,
,![]() ,
,![]() ,
,![]() .
.
3.10
![]() ,
,![]() .
.
3.11
![]() ,
,![]() .
.
3.12
![]() ,
,![]() .
.
3.13
![]() ,
,![]() .
.
3.14
![]() ,
,![]() .
.
3.15
![]() ,
,![]() .
.
3.16
![]() ,
,![]() .
.
3.17
![]() ,
,![]() .
.
3.18
![]() ,
,![]() .
.
3.18
![]() ,
,![]() .
.
3.19
![]() ,
,![]() .
.
3.20
![]() ,
,![]() .
.
3.21
![]() ,
,![]() .
.
3.22
![]() ,
,![]() .
.
3.23
![]() ,
,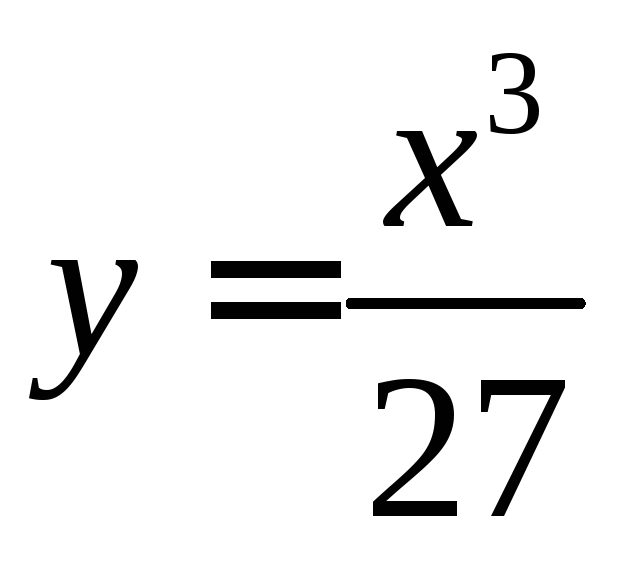 .
.
3.24
![]() ,
,![]() .
.
3.25
![]() ,
,![]() .
.
3.26
![]() ,
,![]() ,
,![]() .
.
3.27
![]() .
.
3.28
![]() ,
,![]() .
.
3.29
![]() ,
,![]() .
.
3.30
![]() ,
,![]() .
.
Задание 4. Вычислить несобственный интеграл или установить его расходимость.
4.1
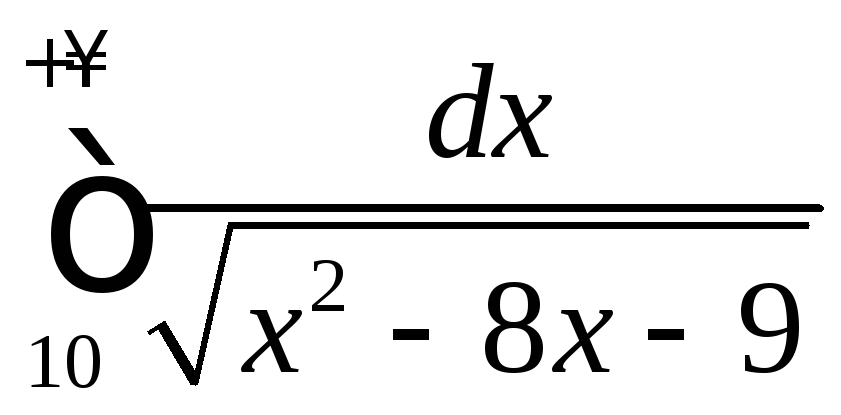 .
.
4.2
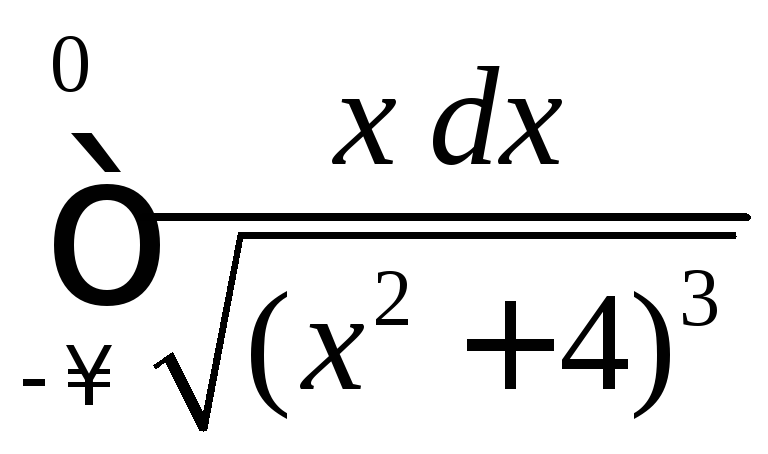 .
.
4.3
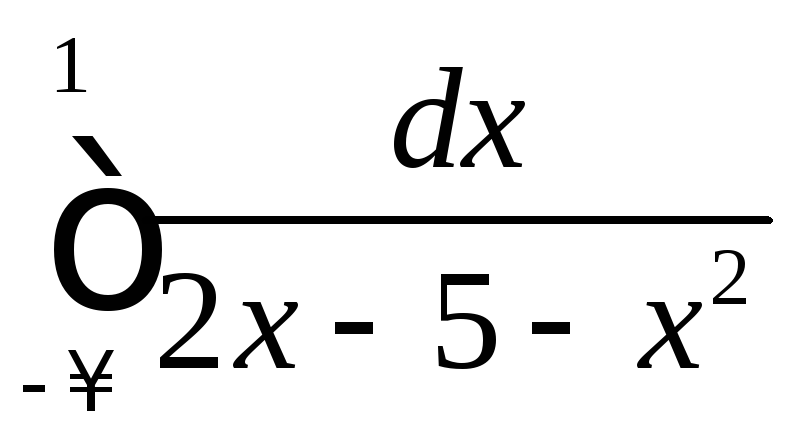 .
.
4.4
 .
.
4.5
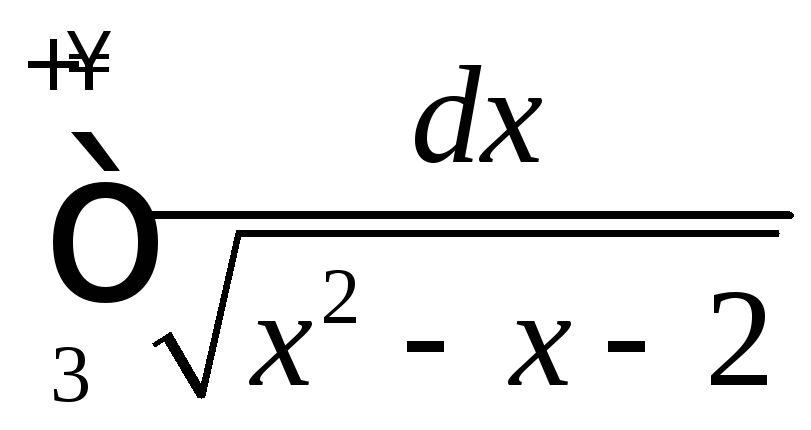 .
.
4.6
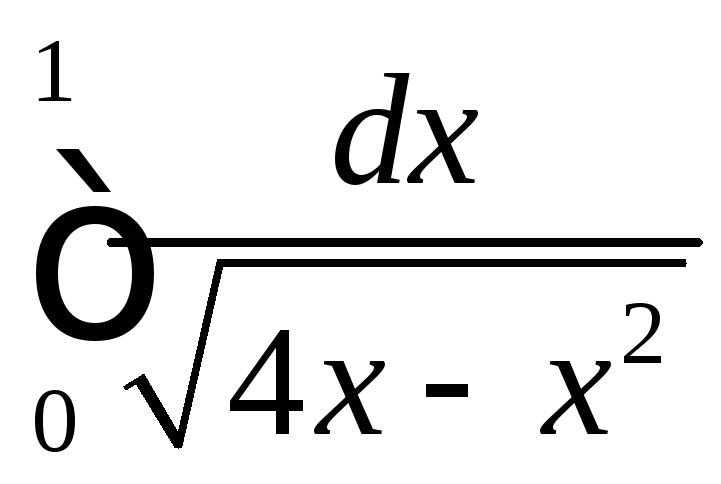 .
.
4.7
 .
.
4.8
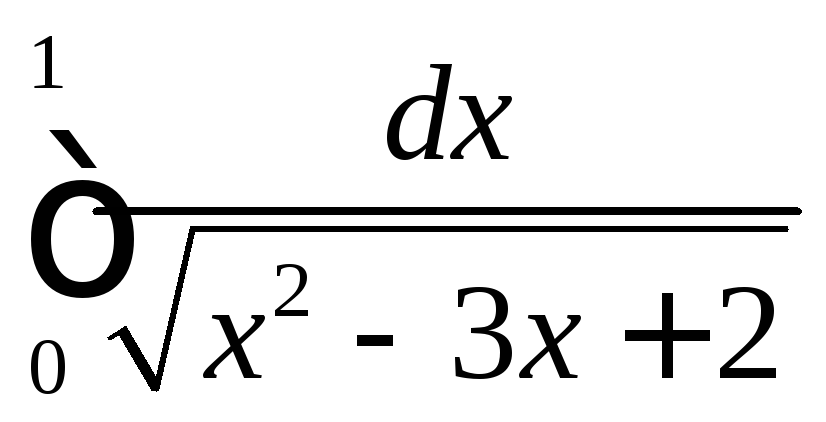 .
.
4.9
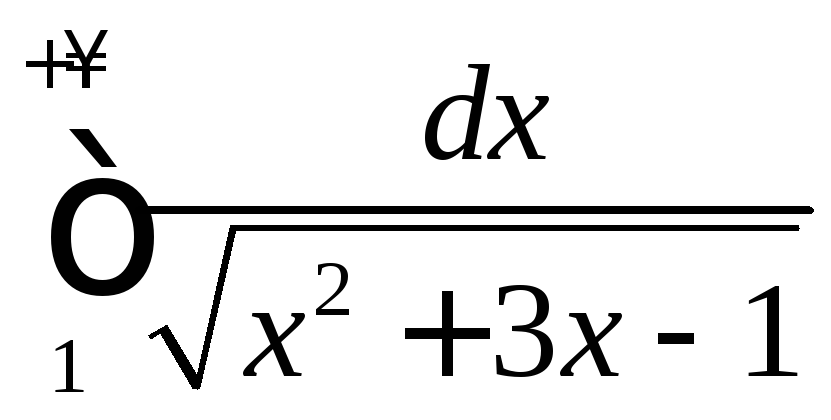 .
.
4.10
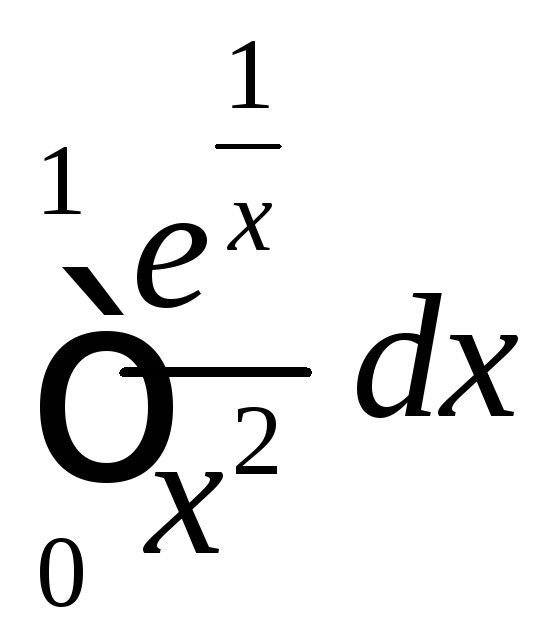 .
.
4.11
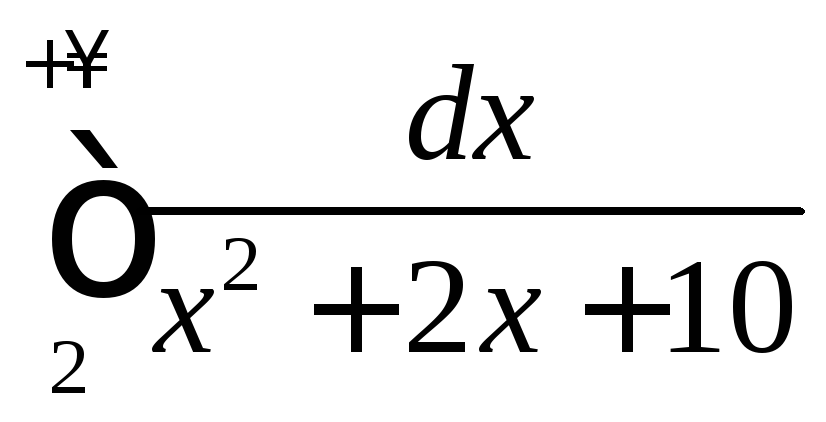 .
.
4.12
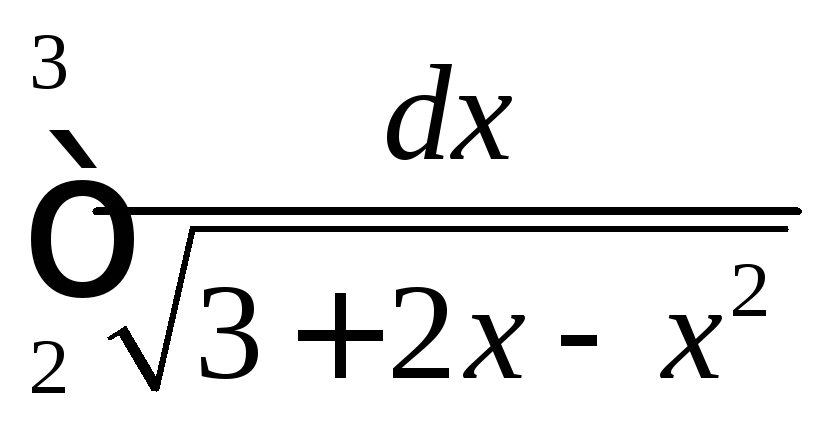 .
.
4.13
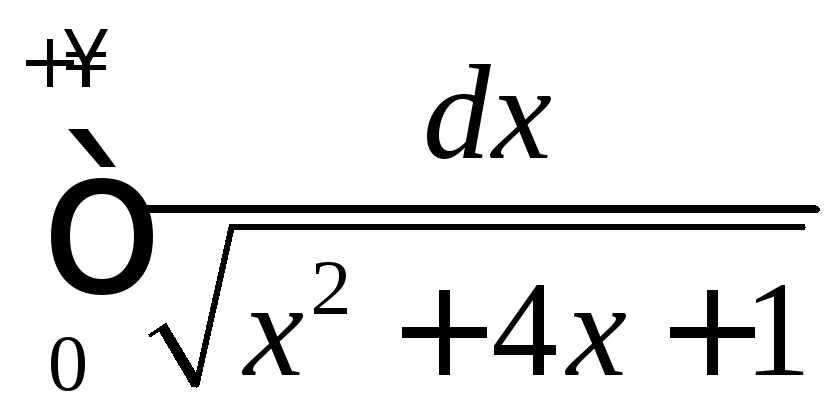 .
.
4.14
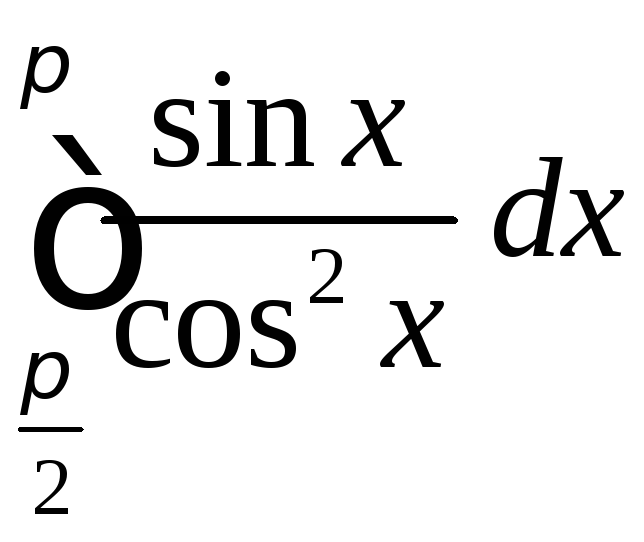 .
.
4.15
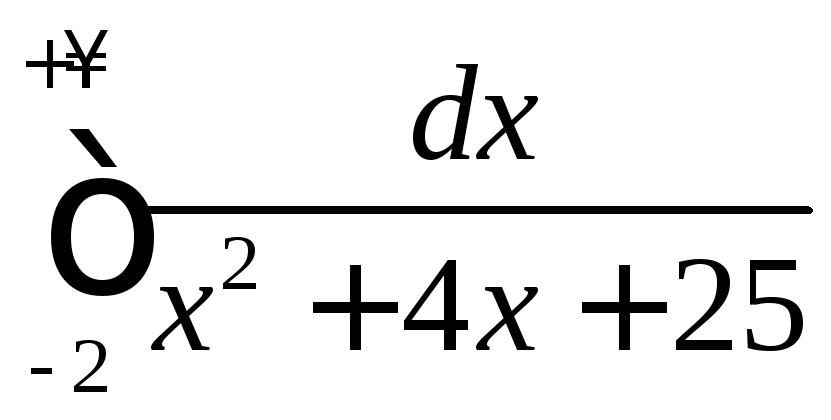 .
.
4.16
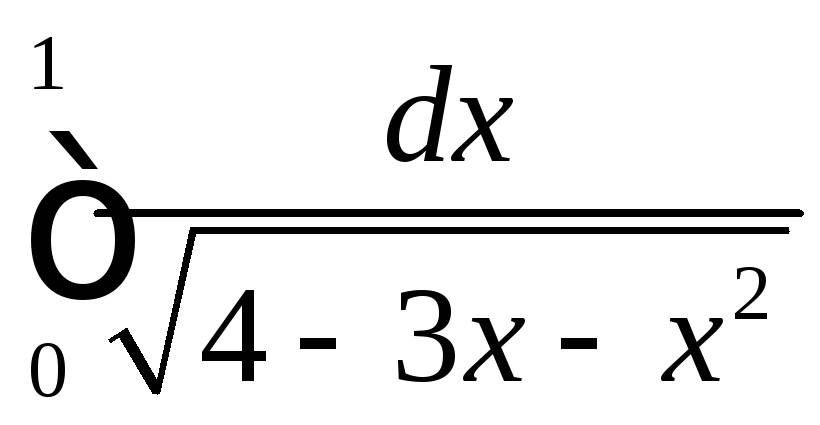 .
.
4.17
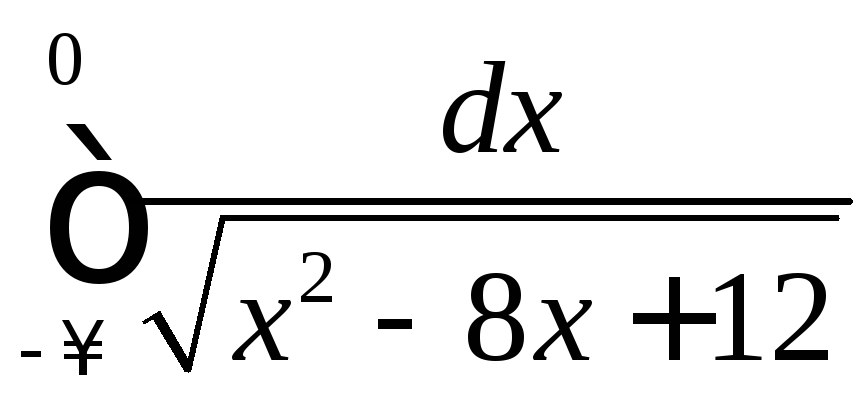 .
.
4.18
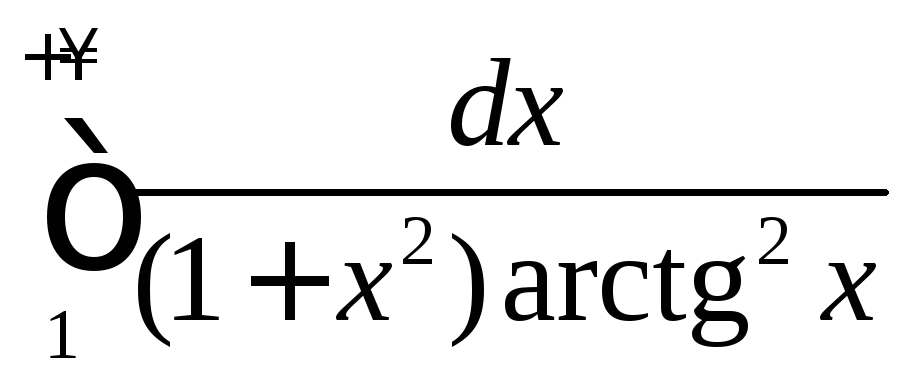 .
.
4.19
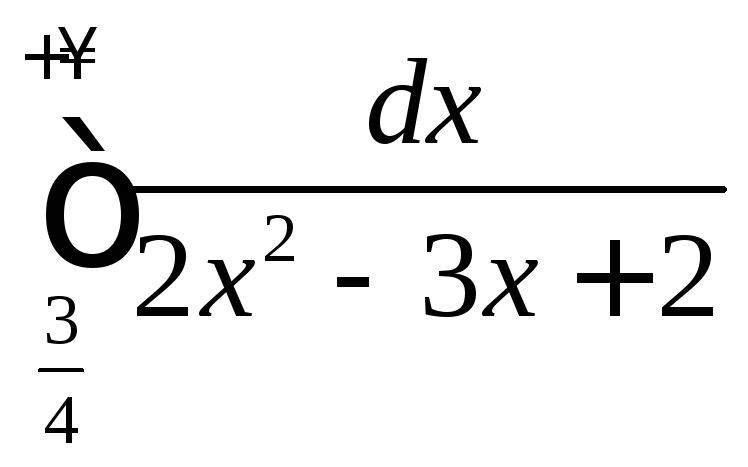 .
.
4.20
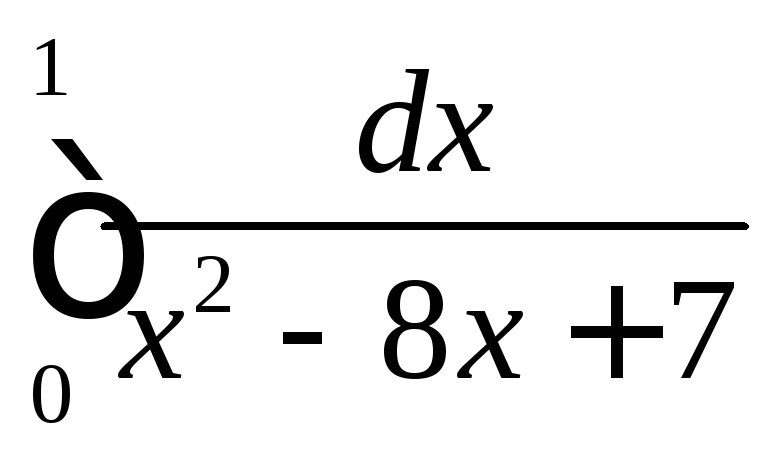 .
.
4.21
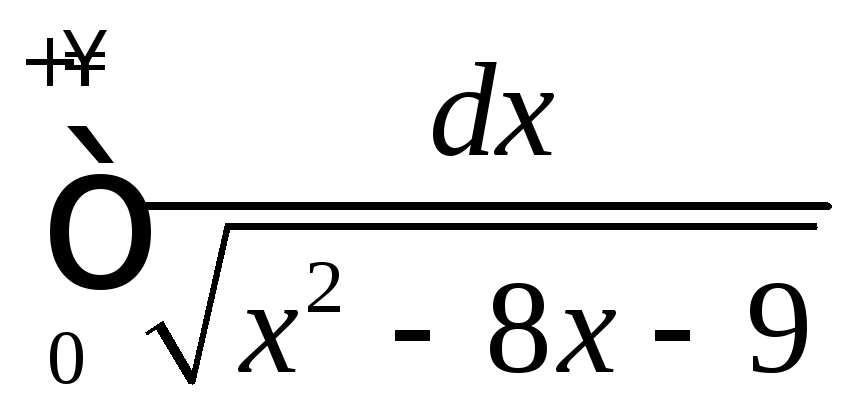 .
.
4.22
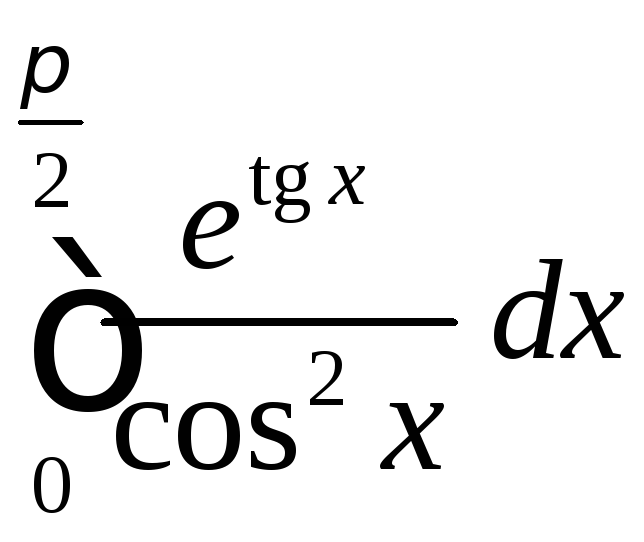 .
.
4.23
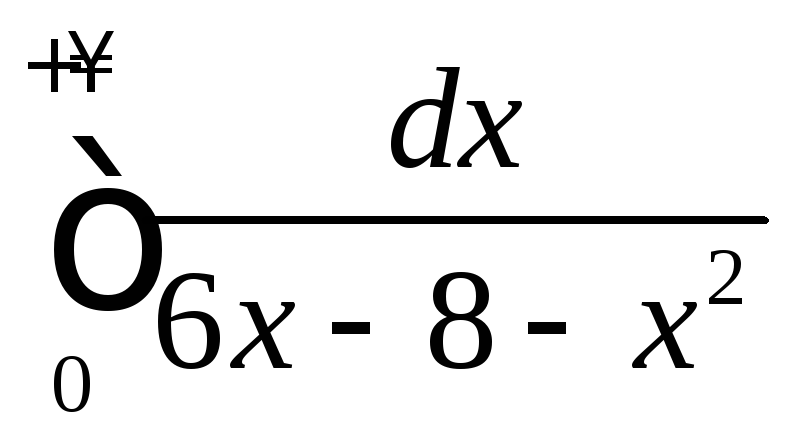 .
.
4.24
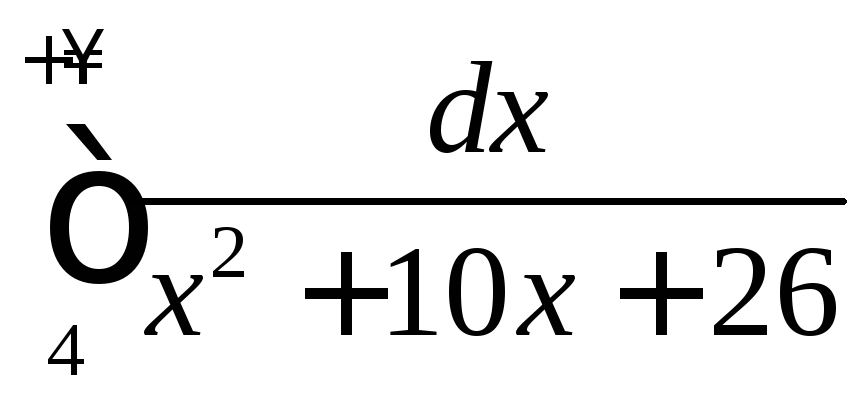 .
.
4.25
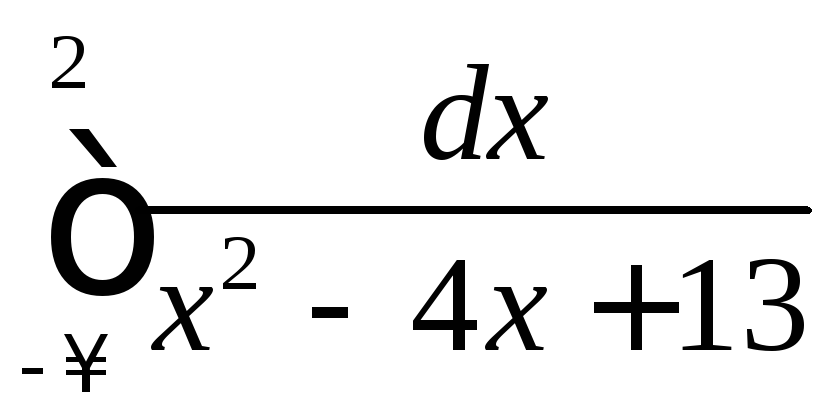 .
.
4.26
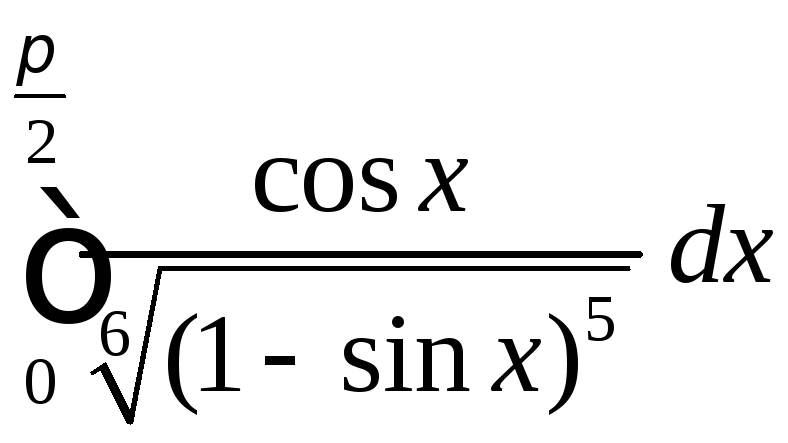 .
.
4.27
 .
.
4.28
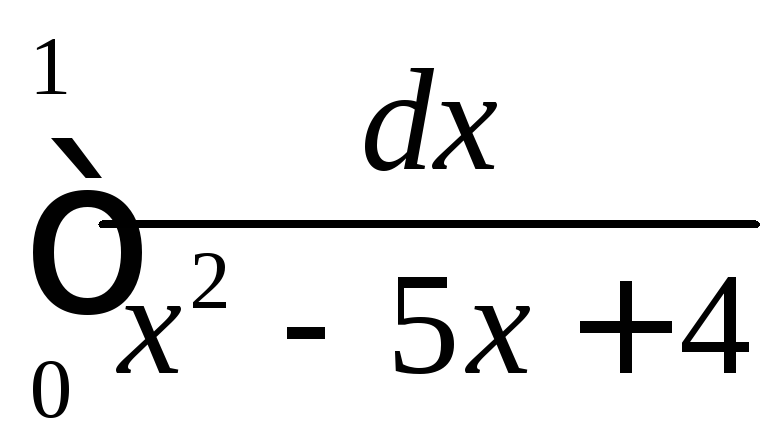 .
.
4.29
 .
.
4.30
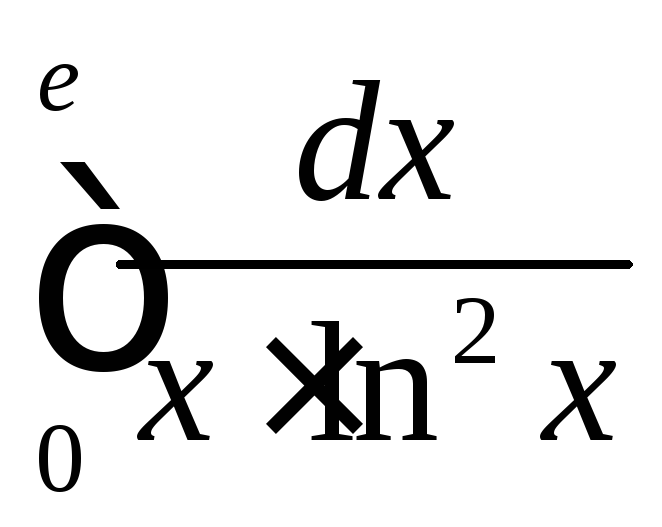 .
.
Задание 5. Найти частные производные и полный дифференциал первого порядка функции.
5.1
![]() .
.
5.2
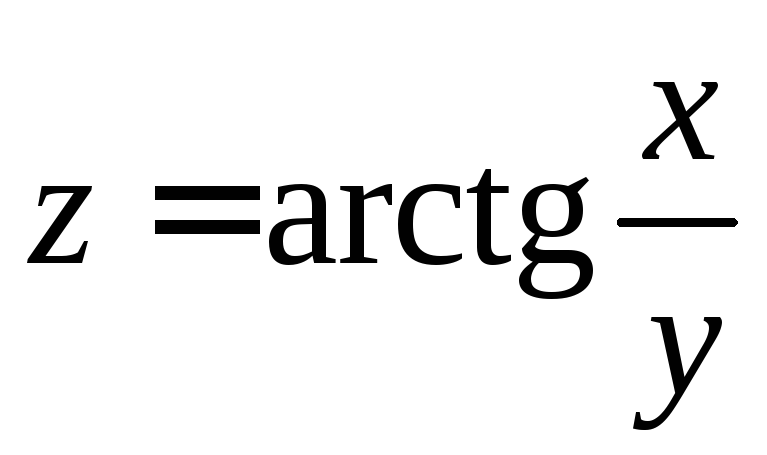 .
.
5.3
![]() .
.
5.4
![]() .
.
5.5
![]() .
.
5.6
![]() .
.
5.7
![]() .
.
5.8
![]() .
.
5.9
![]() .
.
5.10
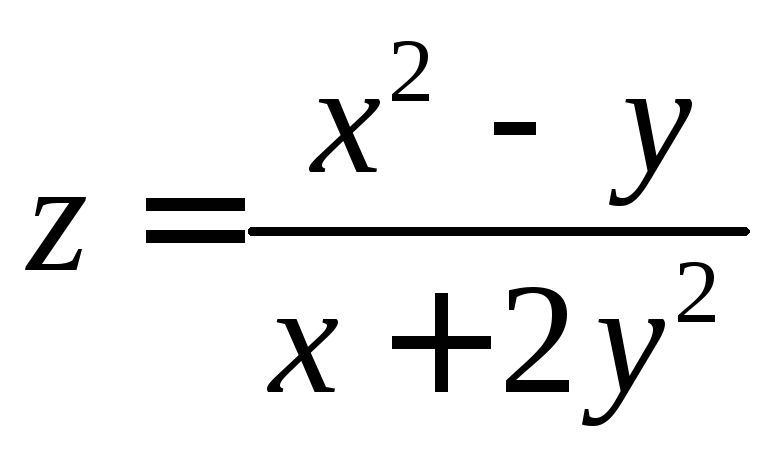 .
.
5.11
![]() .
.
5.12
![]() .
.
5.13
![]() .
.
5.14
![]() .
.
5.15
![]() .
.
5.16
![]() .
.
5.17
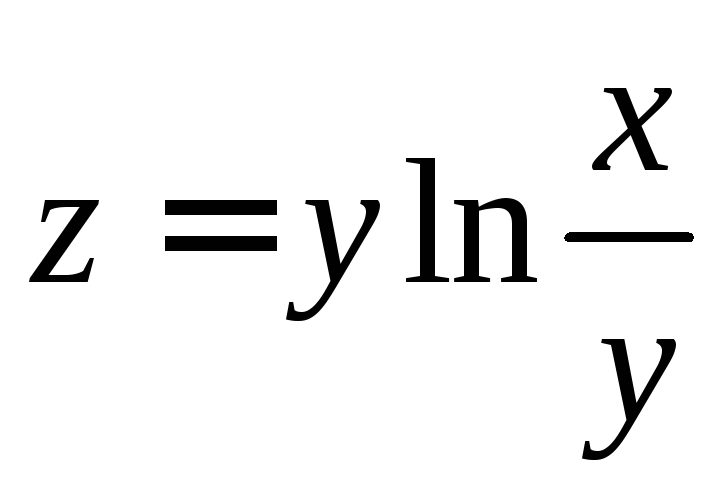 .
.
5.18
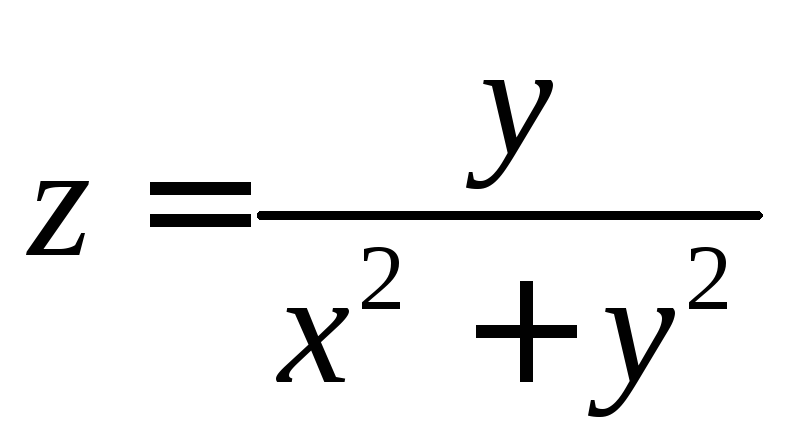 .
.
5.19
![]() .
.
5.20
![]() .
.
5.21
![]() .
.
5.22
![]() .
.
5.23
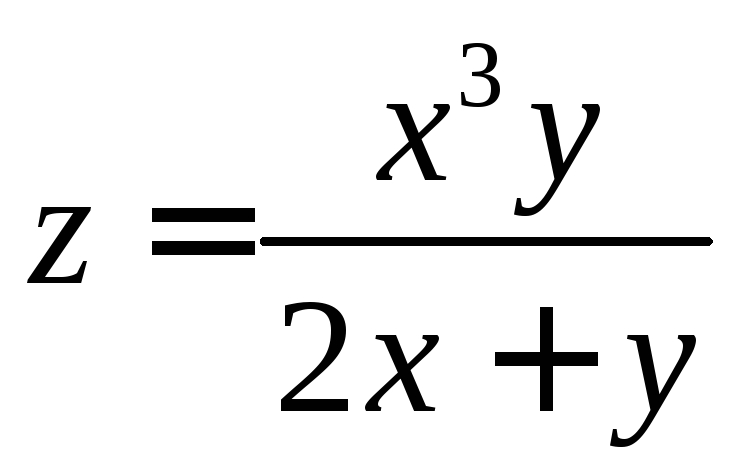 .
.
5.24
![]() .
.
5.25
![]() .
.
5.26
![]() .
.
5.27
![]() .
.
5.28
![]() .
.
5.29
![]() .
.
5.30
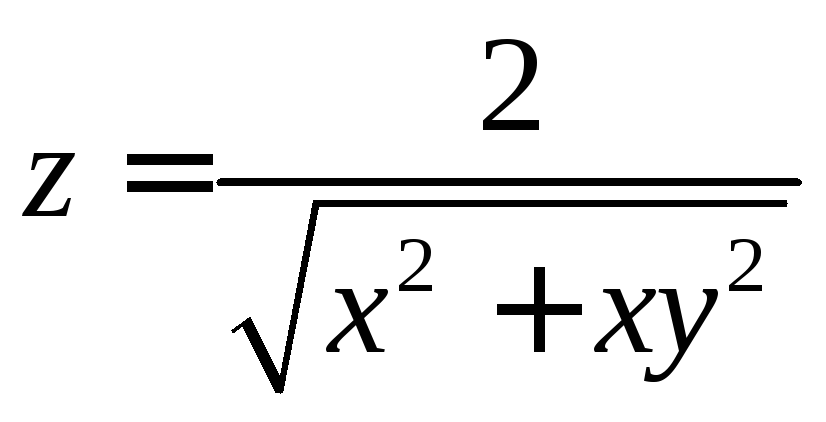 .
.
Задание 6. Исследовать на экстремумы функции.
6.1
![]() .
.
6.2
![]() .
.
6.3
![]() .
.
6.4
![]() .
.
6.5
![]() .
.
6.6
![]() .
.
6.7
![]() .
.
6.8
![]() .
.
6.9
![]() .
.
6.10
![]() .
.
6.11
![]() .
.
6.12
![]() .
.
6.13
![]() .
.
6.14
![]() .
.
6.15
![]() .
.
6.16
![]() .
.
6.17
![]() .
.
6.18
![]() .
.
6.19
![]() .
.
6.20
![]() .
.
6.21
![]() .
.
6.22
![]() .
.
6.23
![]() .
.
6.24
![]() .
.
6.25
![]() .
.
6.26
![]() .
.
6.27
![]() .
.
6.28
![]() .
.
6.29
![]() .
.
6.30
![]() .
.
Задание 7. Вычислить двойной интеграл по области D, ограниченной указанными линиями.
|
7.1 |
|
|
|
7.2 |
|
|
|
7.3 |
|
|
|
7.4 |
|
|
|
7.5 |
|
|
|
7.6 |
|
|
|
7.7 |
|
|
|
7.8 |
|
|
|
7.9 |
|
|
|
7.10 |
|
|
|
7.11 |
|
|
|
7.12 |
|
|
|
7.13 |
|
|
|
7.14 |
|
|
|
7.15 |
|
|
|
7.16 |
|
|
|
7.17 |
|
|
|
7.18 |
|
|
|
7.19 |
|
|
|
7.20 |
|
|
|
7.21 |
|
|
|
7.22 |
|
|
|
7.23 |
|
|
|
7.24 |
|
|
|
7.25 |
|
|
|
7.26 |
|
|
|
7.27 |
|
|
|
7.28 |
|
|
|
7.29 |
|
|
|
7.30 |
|
|
Задание
8. Вычислить
тройной интеграл по области
![]() ,
ограниченной указанными поверхностями,
перейдя к цилиндрическим координатам.
,
ограниченной указанными поверхностями,
перейдя к цилиндрическим координатам.
|
8.1 |
|
|
|
8.2 |
|
|
|
8.3 |
|
|
|
8.4 |
|
|
|
8.5 |
|
|
|
8.6 |
|
|
|
8.7 |
|
|
|
8.8 |
|
|
|
8.9 |
|
|
|
8.10 |
|
|
|
8.11 |
|
|
|
8.12 |
|
|
|
8.13 |
|
|
|
8.14 |
|
|
|
8.15 |
|
|
|
8.16 |
|
|
|
8.17 |
|
|
|
8.18 |
|
|
|
8.19 |
|
|
|
8.20 |
|
|
|
8.21 |
|
|
|
8.22 |
|
|
|
8.23 |
|
|
|
8.24 |
|
|
|
8.25 |
|
|
|
8.26 |
|
|
|
8.27 |
|
|
|
8.28 |
|
|
|
8.29 |
|
|
|
8.30 |
|
|
Задание 9. Приложения двойных интегралов к механике.
9.1 Найти координаты
центра масс плоской однородной пластинки,
ограниченной линиями:
![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ).
).
9.2 Вычислить
статический момент относительно оси
![]() однородной плоской фигуры, лежащей в
плоскости
однородной плоской фигуры, лежащей в
плоскости![]() и ограниченной линиями
и ограниченной линиями![]() .
.
9.3 Вычислить момент
инерции относительно начала координат
фигуры плотностью
![]() ,
ограниченной линиями
,
ограниченной линиями![]() .
.
9.4 Вычислить
координаты центра масс однородной
пластины, лежащей в плоскости
![]() и ограниченной линиями
и ограниченной линиями![]() .
.
9.5 Вычислить момент
инерции относительно точки пересечения
диагоналей прямоугольной пластинки
со сторонами 4 и 6, если ее плотность
![]() .
.
9.6 Вычислить момент
инерции относительно оси
![]() пластины плотностью
пластины плотностью![]() ,
лежащей в плоскости
,
лежащей в плоскости![]() и ограниченной линиями
и ограниченной линиями![]() .
.
9.7 Определить
массу фигуры, ограниченной линиями
![]() и
и![]() ,
если плотность распределения масс
,
если плотность распределения масс![]()
9.8 Определить
координаты центра масс области,
ограниченной линиями
![]()
![]() ,
если ее плотность
,
если ее плотность![]() .
.
9.9 Определить
координаты центра масс однородной
пластинки, ограниченной прямой
![]() =0
и одной полуволной синусоиды
=0
и одной полуволной синусоиды
![]() .
.
9.10 Найти статический
момент прямоугольника со сторонами
![]() и
и![]() относительно стороны
относительно стороны![]() если плотность распределения масс в
каждой точке равна произведению
координат этой точки.
если плотность распределения масс в
каждой точке равна произведению
координат этой точки.
9.11 Вычислить
момент инерции относительно начала
координат фигуры, ограниченной линией
![]() ,
если ее плотность
,
если ее плотность![]() .
.
9.12 Вычислить массу
пластинки, ограниченной линией
![]() ,
если поверхностная плотность в каждой
ее точке
,
если поверхностная плотность в каждой
ее точке![]() ,
,
9.13 Вычислить
статический момент однородной пластины,
ограниченной линиями
![]() ,
относительно оси
,
относительно оси![]() .
.
9.14 Определить
координаты центра масс однородной
пластины, ограниченной линиями
![]() .
.
9.15 Определить
статический момент относительно оси
![]() ,
плоской области, ограниченной линиями
,
плоской области, ограниченной линиями![]() если
известно, что плотность распределения
масс в каждой точке
если
известно, что плотность распределения
масс в каждой точке![]() .
.
9.16 Определить
массу плоской фигуры, ограниченной
линиями
![]() если
плотность распределения масс
если
плотность распределения масс![]() .
.
9.17 Вычислить
момент инерции круга, радиуса
![]() ,
относительно начала координат.
,
относительно начала координат.
9.18 Вычислить
момент инерции плоской фигуры,
ограниченной линиями
![]() ,
,![]() ,
,![]() относительно оси
относительно оси![]() ,
если поверхностная плотность в каждой
точке
,
если поверхностная плотность в каждой
точке![]() .
.
9.19 Определить
массу пластинки, имеющей форму круга
с радиусом
![]() ,
если плотность в любой точке обратно
пропорциональна расстоянию от этой
точки до центра круга.
,
если плотность в любой точке обратно
пропорциональна расстоянию от этой
точки до центра круга.
9.20 Найти статический
момент относительно оси
![]() однородной пластинки, ограниченной
линиями
однородной пластинки, ограниченной
линиями![]() ,
,![]() .
.
9.21 Найти момент
инерции однородного треугольника,
ограниченного прямыми
![]() ,
,![]() ,
,![]() относительно оси
относительно оси![]() .
.
9.22 Найти статический
момент относительно оси
![]() треугольника, ограниченного прямыми
треугольника, ограниченного прямыми![]() ,
,![]() ,
,![]() ,
если плотность его в каждой точке равна
ординате этой точки.
,
если плотность его в каждой точке равна
ординате этой точки.
9.23 Найти статический
момент относительно оси
![]() однородной фигуры, ограниченной линиями
однородной фигуры, ограниченной линиями![]() ,
,![]() .
.
9.24 Вычислить массу
пластинки, ограниченной линиями
![]() ,
если поверхностная плотность в каждой
ее точке
,
если поверхностная плотность в каждой
ее точке![]() .
.
9.25 Найти координаты
центра масс однородной пластинки,
ограниченной линиями
![]() .
.
9.26 Вычислить массу
пластинки, ограниченной линиями
![]() ,
если плотность ее в каждой точке равна
сумме координат этой точки.
,
если плотность ее в каждой точке равна
сумме координат этой точки.
9.27 Вычислить массу
пластинки, ограниченной линиями
![]() ,
если поверхностная плотность в каждой
ее точке
,
если поверхностная плотность в каждой
ее точке![]() .
.
9.28 Вычислить
момент инерции однородной пластинки,
ограниченной линиями
![]() относительно оси
относительно оси![]() .
.
9.29 Найти координаты
центра масс однородной пластинки,
ограниченной линиями
![]() .
.
9.30 Вычислить
момент инерции относительно оси
![]() однородной пластинки, ограниченной
линиями
однородной пластинки, ограниченной
линиями![]() .
.

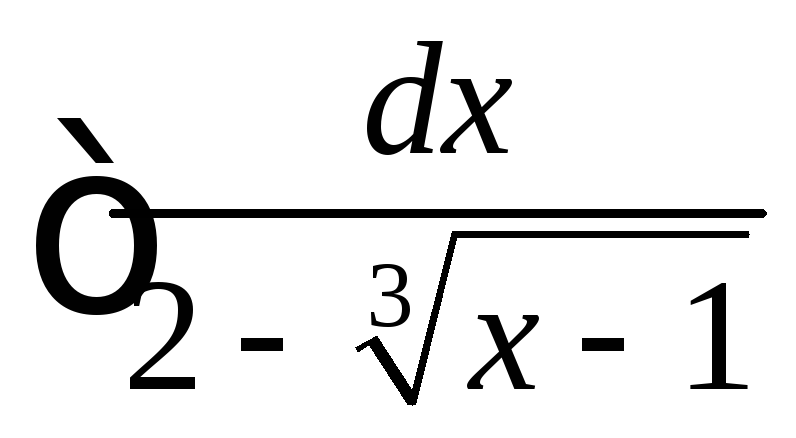 .
.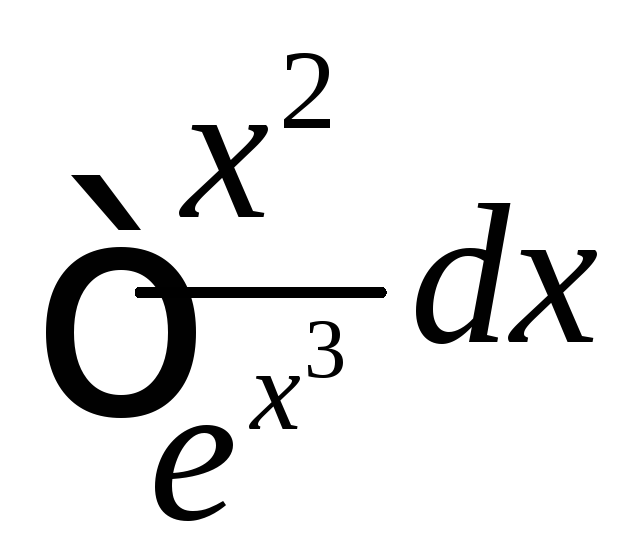 ,
,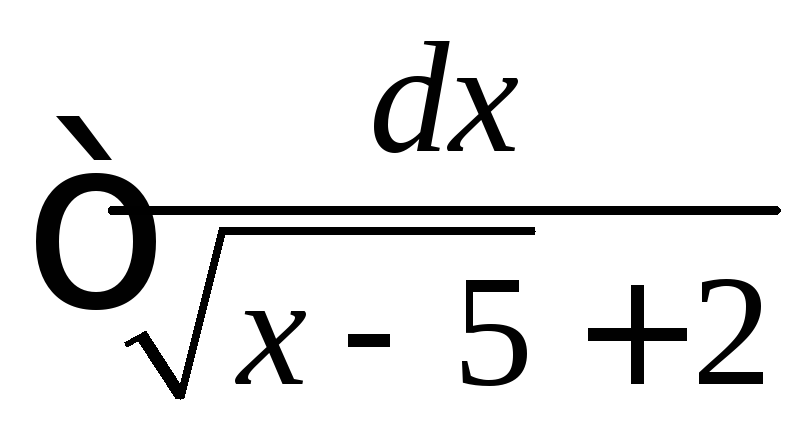 .
.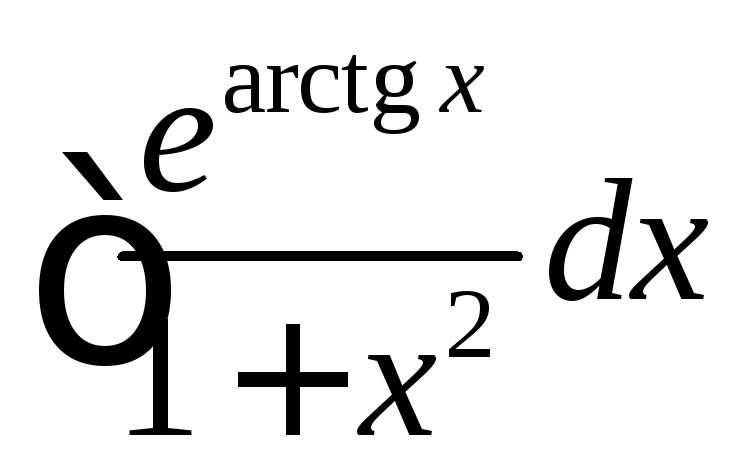 ,
,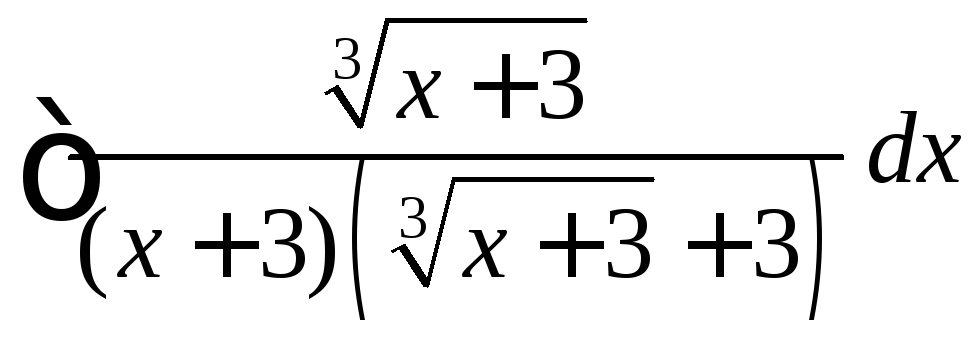 .
.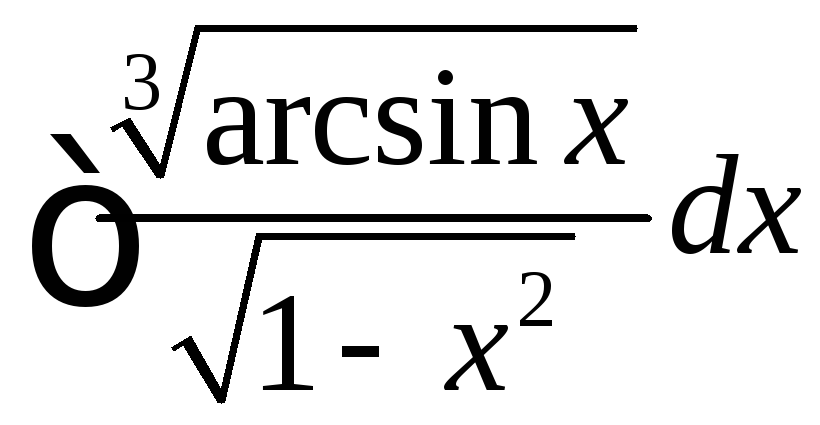 ,
,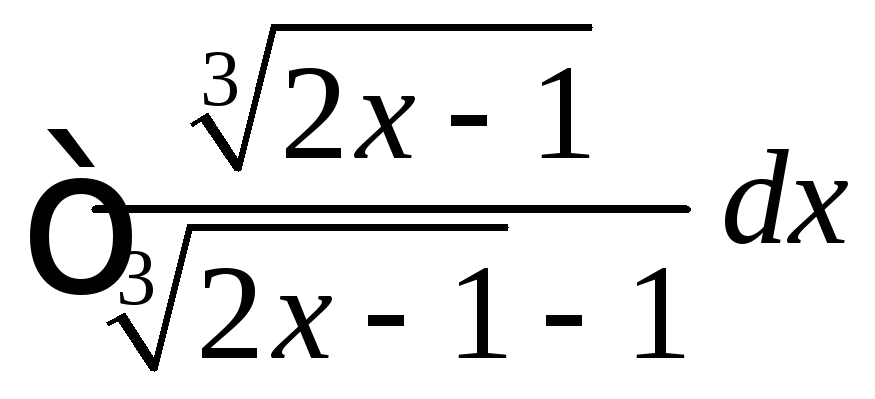 .
.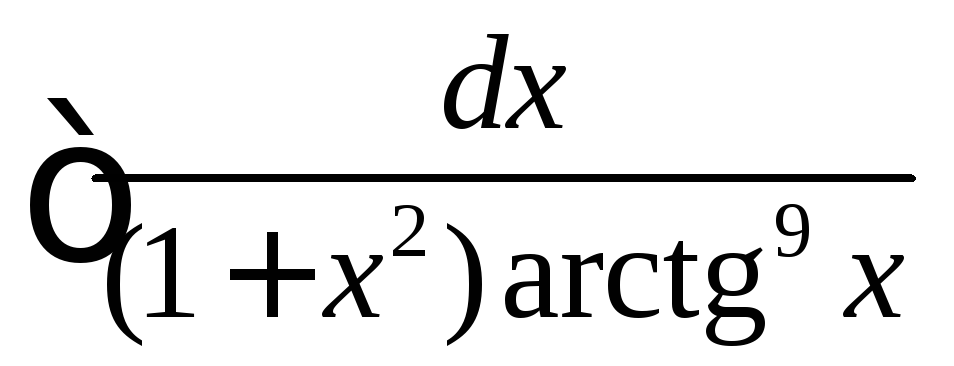 ,
,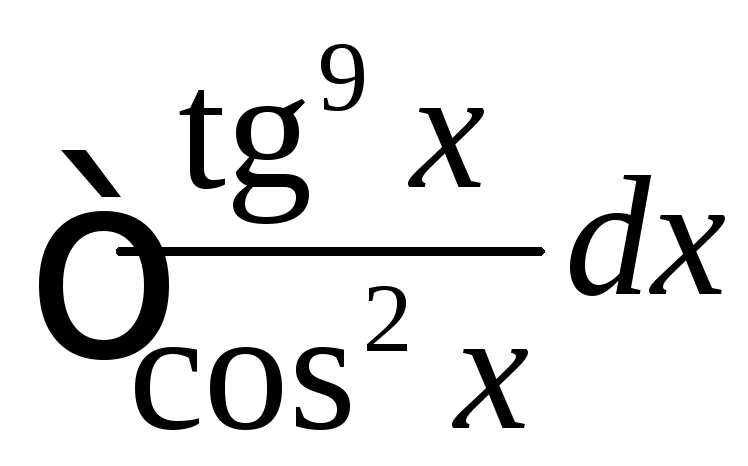 ,
,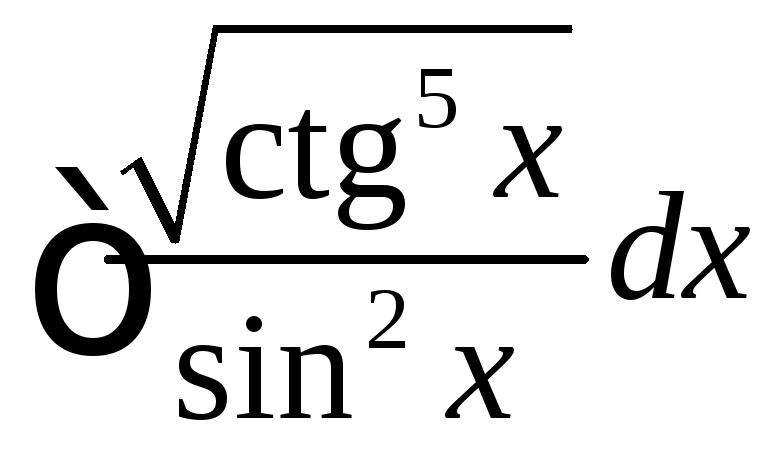 ,
,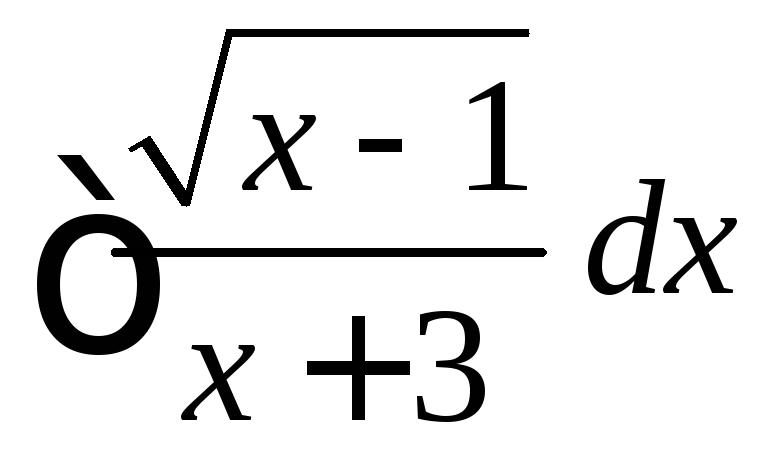 .
.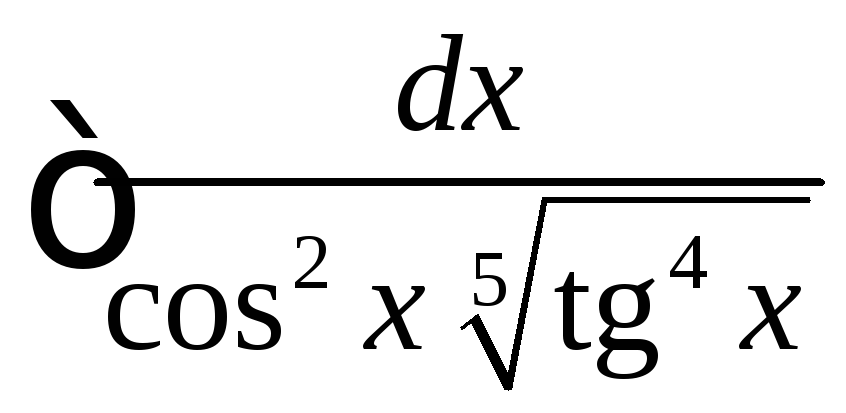 ,
,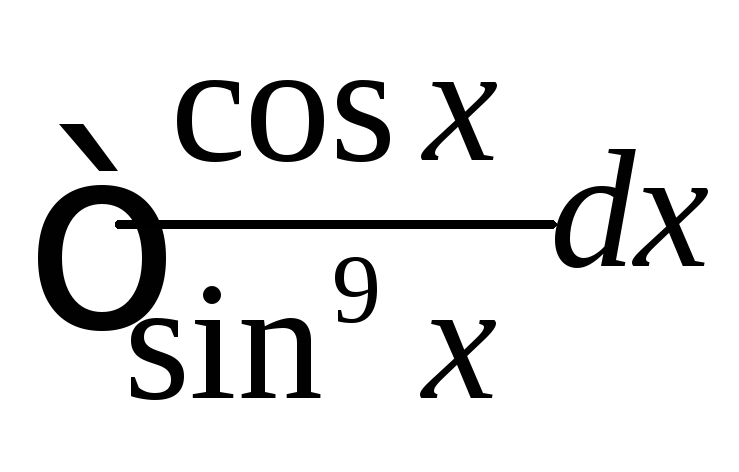 ,
,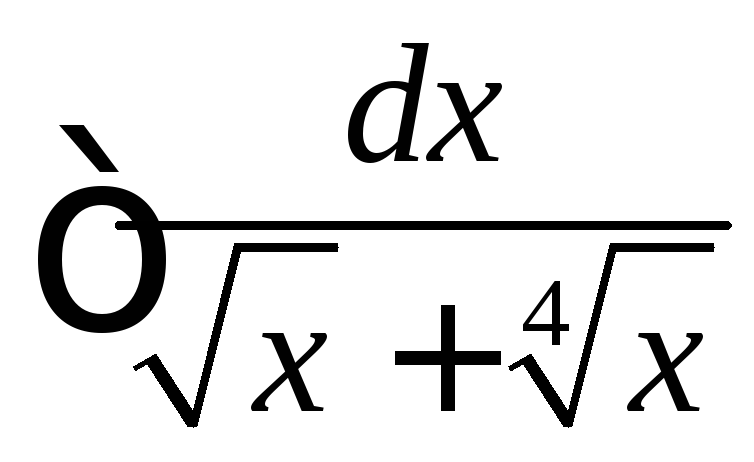 .
.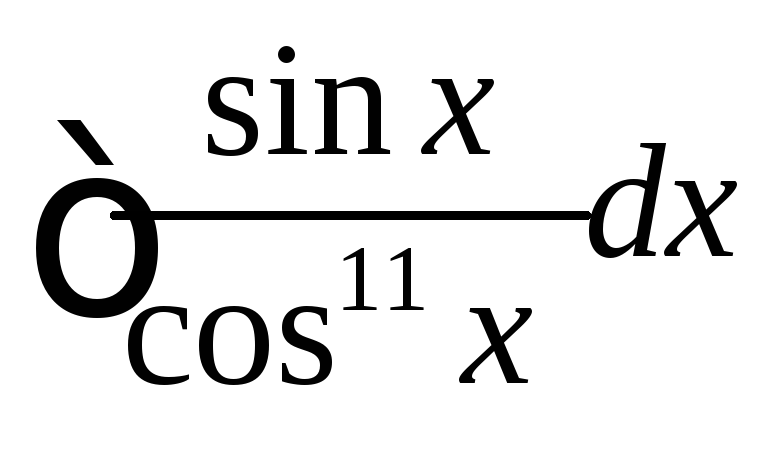 ,
,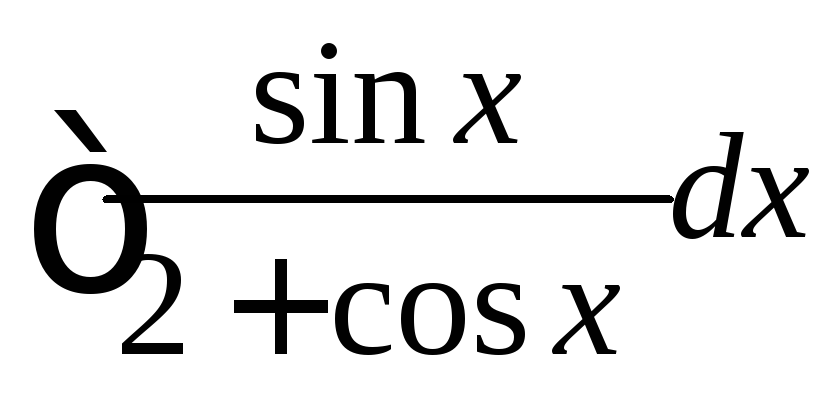 ,
,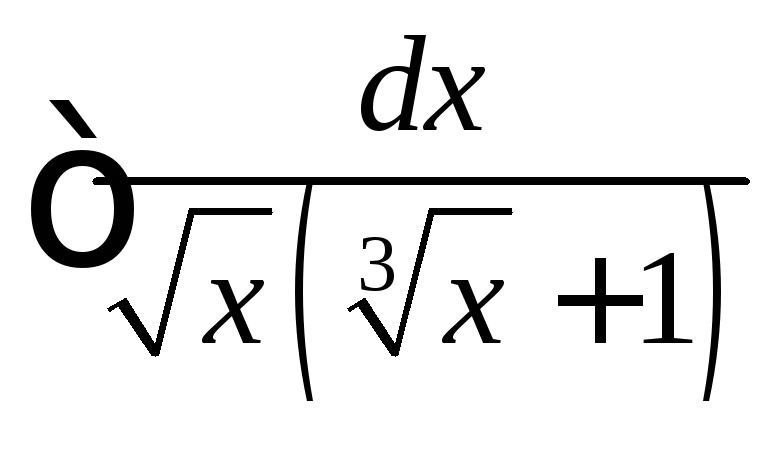 .
.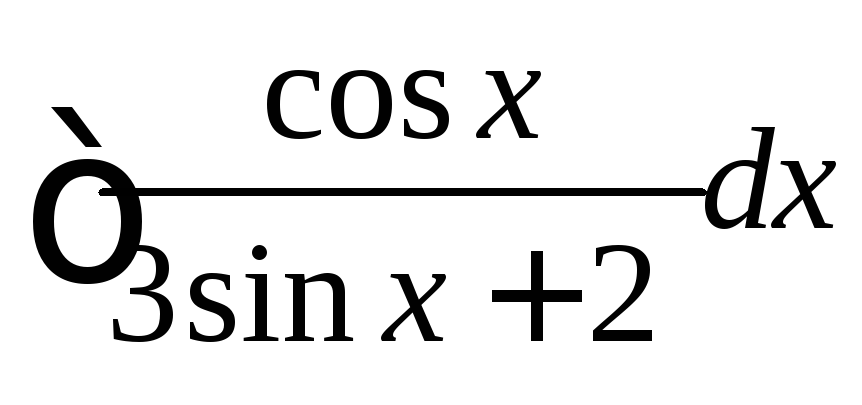 ,
,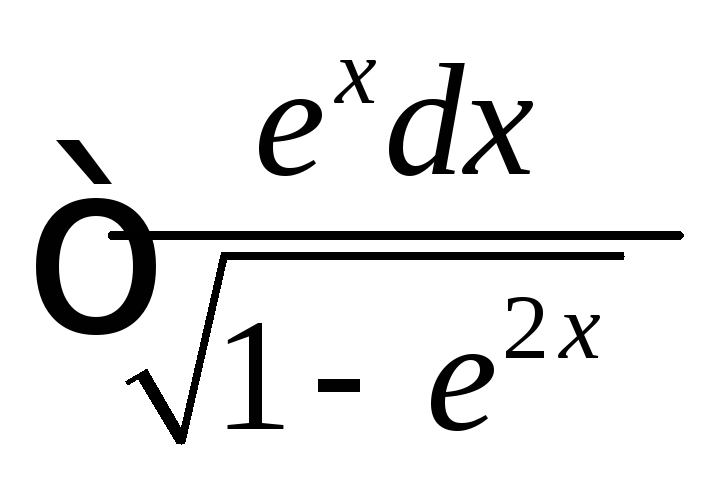 ,
,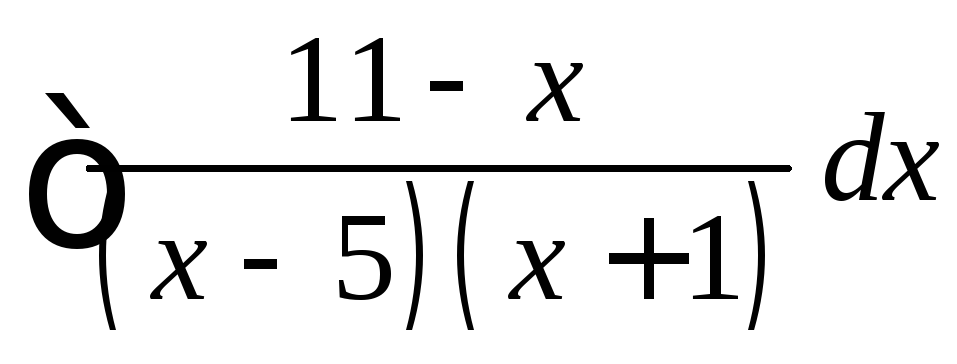 ,
,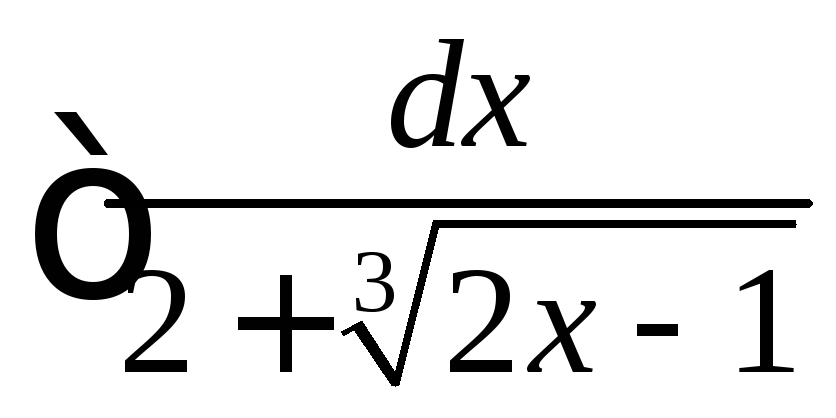 .
.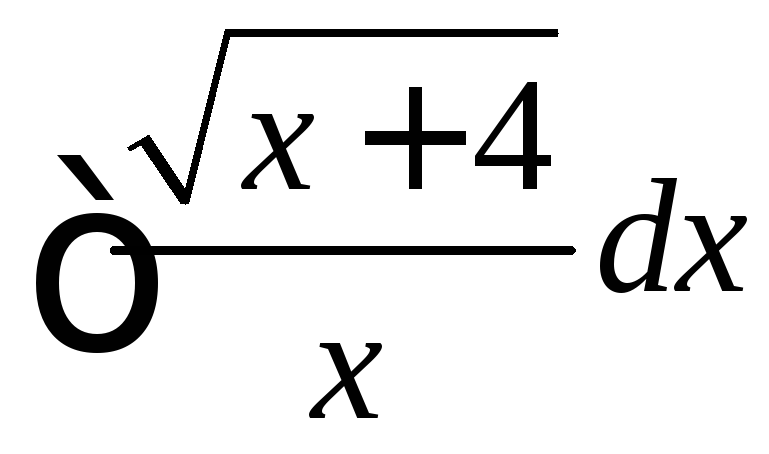 .
.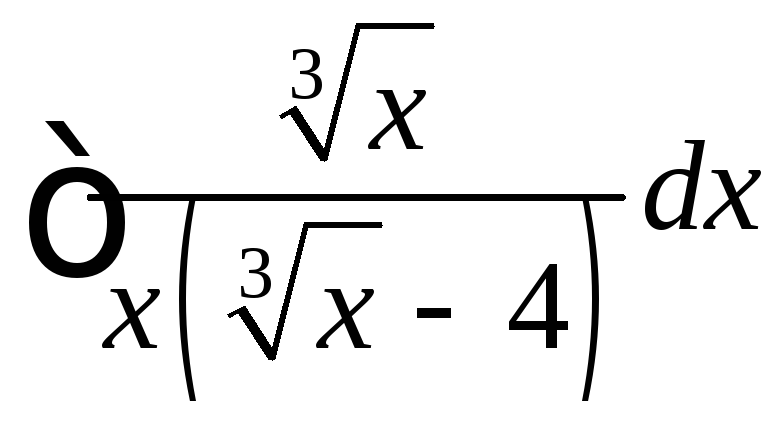 .
.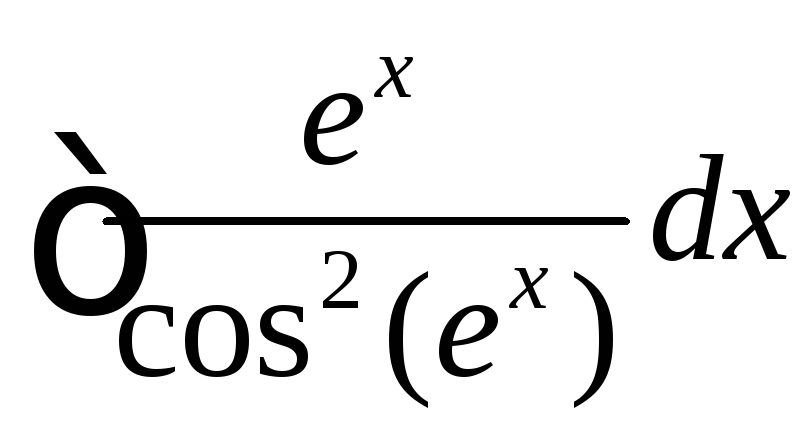 ,
,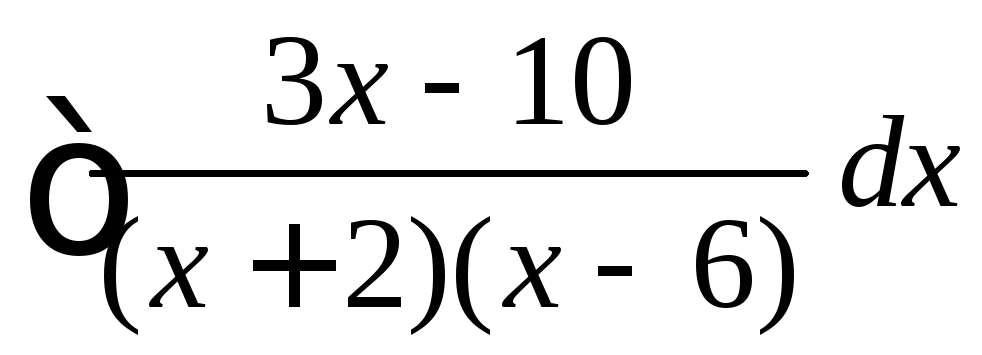 ,
,