
Лабораторная работа №3
.pdf
ЛАБОРАТОРНАЯ РАБОТА №5
Поиск оптимальных решений Краткий комментарий
Многие проблемы производства, проектирования, прогнозирования сводятся к широкому классу задач оптимизации, для решения которых применяются методы математического программирования. Математическую модель оптимизационной задачи (задачи математического программирования) можно представить в следующем виде:
Целевая функция: Z (x1, x2 ,..., xn ) ® max(min, const ) ,
Ограничения: gi (x) £ (³, =)bi
Граничные условия: d j £ x j £ Dj , i =1, m j =1, n
Целевая функция (ЦФ) – критерий оптимизации, показывает, в каком смысле решение должно быть оптимальным, т.е. наилучшим. При этом возможны три вида назначения целевой функции: максимизация, минимизация, назначение заданного значения.
Ограничения (ОГР) – устанавливают зависимости между
могут быть односторонними ( gi (x)£ bi ) или двусторонними: ( ai £ gi (x)£ bi ,
gi (x)³ ai и gi (x)£ bi ).
Граничные условия (ГРУ) – показывают, в каких пределах могут изменяться значения переменных.
Если целевая функция и ограничения линейны(являются многочленами первой степени относительно переменных), задача относится к области линейного программирования. Особое место в линейном программировании занимают конкретные задачи, среди которых особенно важными для приложений являются задачи транспортного типа. Для решения этих задач созданы специальные вычислительные методы, учитывающие специфическую структуру их ограничений. А также задачи целочисленного линейного программирования, в которых на переменные накладывается дополнительное требование целочисленности.
В MS Excel существует возможность с помощью надстройки Поиск решения найти решение, оптимальное в некотором смысле при нескольких входных значениях и наборе ограничений на решение. С помощью надстройки Поиск решения можно решать как линейные задачи (задачи линейного, целочисленного и стохастического программирования), так и нелинейные (задачи нелинейного программирования).
Задача линейной оптимизации
Постановка задачи
Минимизировать функцию Z=-x1+3x2+2x3 при ограничениях:
ì x |
+ x |
|
+ |
2x |
|
³ -5, |
|
|||||
ï |
1 |
|
|
2 |
|
|
|
3 |
|
|
|
|
í |
2x1 - 3x2 + x3 £ 3, |
|
||||||||||
ï2x |
|
- 5x |
2 |
+ 6x |
3 |
£ 5, |
|
|||||
î |
1 |
|
|
|
|
|
|
|
|
|||
x j |
£ 0 |
|
|
(j =1,2,3). |
|
|||||||
Математическая модель |
|
|||||||||||
ЦФ: |
|
|
Z=-x1+3x2+2x3→min |
|
||||||||
|
|
|
|
|
Корпоративные информационные системы Финансы и кредит |
1 |
||||||
ОГР:
ГРУ:
ìï x1 + x2 + 2 x3 ³ -5, í 2x1 - 3x2 + x3 £ 3,
ïî2x1 - 5x2 + 6x3 £ 5,
( j = 1,2,3).
Разработка и создание электронной модели
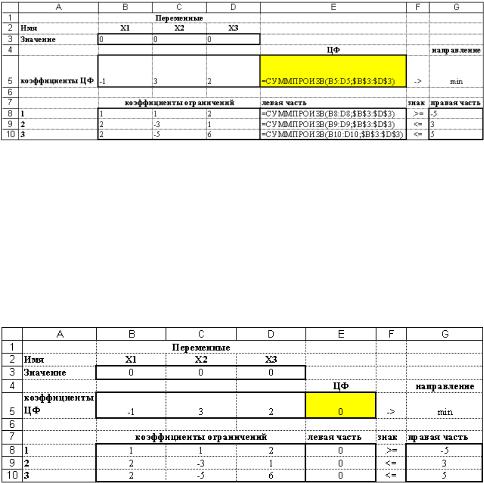
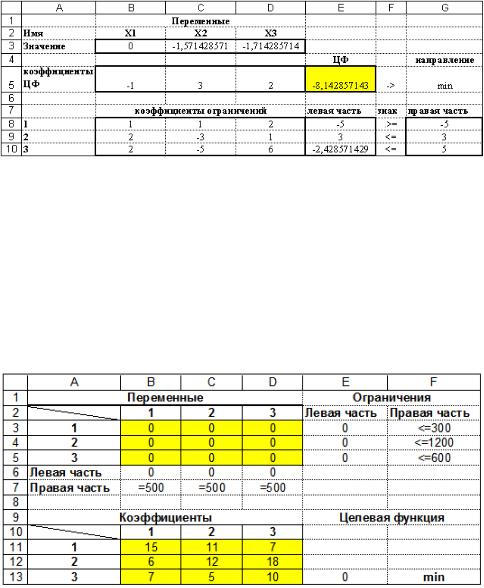
Электронная модель – это электронная таблица Microsoft Excel. Она является отражением математической модели и должна содержать все ее элементы: параметры модели (коэффициенты целевой функции, коэффициенты ограничений), переменные модели, целевую функцию и ограничения. Электронная модель рассматриваемой задачи, в режиме отображения формул, имеет следующий вид:
Поясним содержание некоторых ячеек таблицы.
В блоке B3:C3 находятся искомые значения x1, x2, x3, которые до выполнения поиска решения равны 0. Ячейки блока выполняют роль переменных целевой функции и ограничений. Блок ячеек B5:D5 содержит коэффициенты целевой функции. В блоках B8:D10 и G8:G10 находятся данные соответствующие коэффициентам ограничений и параметрам правой части ограничений. Формулы, реализующие целевую функцию, и левую часть ограничений расположены соответственно в ячейкеE5 и ячейках E8, E9, E10. Обратите внимание, что для ввода целевой функции и ограничений используется встроенная функция Microsoft Excel категории математические
– СУММПРОИЗВ(массив1;массив2), которая возвращает сумму произведений соответствующих элементов массивов или диапазонов.
Электронная таблица в режиме отображения значений имеет следующий вид:
Поиск оптимального решения
Для поиска оптимальных решений вMicrosoft Excel используется надстройка Поиск решения. Поскольку данным средством пользуются не все категории пользова-
Корпоративные информационные системы Финансы и кредит |
2 |
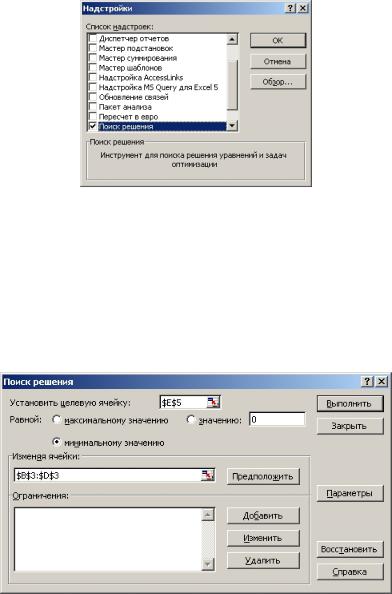
телей, она загружается по мере необходимости и выгружается после завершения работы с приложением. Для загрузки надстройки выполните команду менюСервисÞНадстройки, в диалоговом окне Надстройки установите флажокПоиск решения и нажмите кнопку <OK>.
Технология работы с надстройкой Поиск решения
1.Выполнить команду меню СервисÞПоиск решения.
2.В открывшемся окне диалога:
–в поле Установить целевую ячейку: установить ссылку на ячейку содержащую целевую функцию (Z) – E5.
–в группе Равной: установить переключатель в нужное положение, в зависимости от того, должно ли в результате оптимизации значение целевой ячейки быть максимальным, минимальным или же равняться определенному заданному значению, в нашем случае: минимальному значению.
–в поле Изменяя ячейки: указать диапазон ячеек содержащий неизвестные значения (x1, x2, x3): B3:D3.
– в списке Ограничения: нужно задать ограничения и граничные условия, для этого необходимо нажать кнопку <Добавить>. На экране будет отображено окно диалога для определения ограничения. В поле Ссылка на ячейку: указать ссылку
Корпоративные информационные системы Финансы и кредит |
3 |
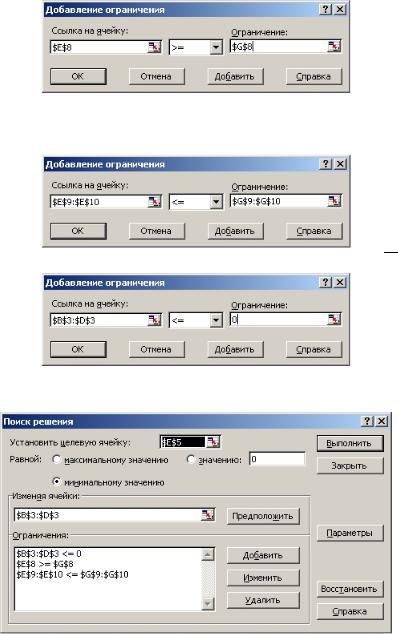
на ячейку (или диапазон), для которой должно действовать ограничение– левая часть. Выберите из списка нужный оператор: =, <=, >= или цел. Последний, выбирается в случае поиска только целочисленных решений. В поле Ограничение: укажите число или ссылку на ячейку(диапазон ячеек), содержащий значения ограничений – правая часть.
– cледующее ограничение можно ввести, нажав кнопку <Добавить.>. Ограничения удобно задавать поблочно. Поскольку между 2-ым и 3-им ограничениями одинаковый знак удобно было бы записать $E$9:$E$10<=$G$9:$G$10. Знак “<=“ относится к каждой ячейке обоих блоков.
последнее ограничение, это реализация граничных условий: x j £ 0, |
j = 1,3 |
– завершение ввода ограничений– кнопка <ОК>. Окно диалога Поиск решения после ввода ограничений выглядит следующим образом:
Корпоративные информационные системы Финансы и кредит |
4 |
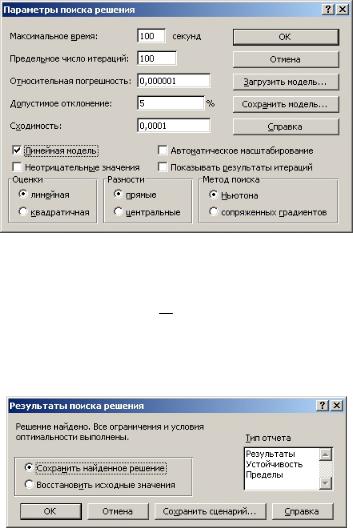
– кнопка <Параметры> позволяет получить доступ к диалоговому окну, в котором можно установить такие параметры, как предельное время выполнения задачи, максимальной число итераций, метод поиска и т.д.
Заметим, что при поиске оптимального решения смысл этих параметров знать -не обязательно, так как их значения, применяемые по умолчанию, обеспечивают нормальное решение практических задач. Однако параметры Линейная модель и Неотрицательные значения рекомендуется устанавливать. В рассматриваемой задаче параметр Неотрицательные значения не установлен, его используют для задания
граничных условий вида x j ³ 0, j =1,3 .
После ввода всех ограничений и установки параметров процедура поиска решений запускается нажатием кнопки <Выполнить>.
Если программа нашла решение, то оно будет отображено в окне диалогаРезуль-
таты поиска решения в виде сообщения.
В этом случае нужно нажать кнопку <OK>, т.е. сохранить найденное решение. Если сообщение другого содержания, нужно установить переключательВосстановить исходные значения, нажать кнопку <OK> и проверить правильность ввода формул в электронную таблицу, ввода параметров в окно диалогаПоиск решения, внести изменения при обнаружении ошибки и повторить операцию поиска оптимального решения.
Корпоративные информационные системы Финансы и кредит |
5 |
Результат поиска решения
Транспортная задача
Постановка задачи
Z (X ) = 15x11 +11x12 + 7x13 +
+6x21 +12x22 +18x23 +
+7x31 + 5x32 +10x33 ® min
ìx |
+ x |
+ x |
£ 300; |
ìx |
+ x |
+ x |
= 500; |
||
ï |
11 |
12 |
13 |
|
|
ï 11 |
21 |
31 |
= 500; |
íx21 + x22 + x23 £1200; |
íx12 |
+ x22 + x32 |
|||||||
ïx |
+ x |
+ x |
£ 600; |
ïx |
+ x |
+ x |
= 500; |
||
î |
31 |
32 |
33 |
|
|
î 13 |
23 |
33 |
|
xij |
³ 0, |
i, j = |
|
|
|
|
|
|
|
1,3. |
|
|
|
|
|||||
Электронная таблица в режиме отображения значений:
Корпоративные информационные системы Финансы и кредит |
6 |
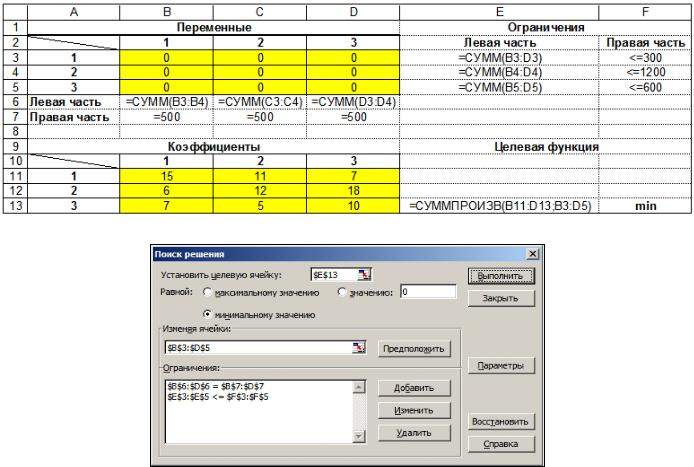
Электронная таблица в режиме отображения формул
Параметры поиска решения
7

Результат поиска решения
Задача нелинейного программирования
Постановка задачи
Z (x) = - 2x1 + x2 + 2 ® min, x1 + 3x2 + 4
ì- x1 + x2 £ 4,
í
î2x1 + x2 £10,
x1 , x2 ³ 0.
При решении задач нелинейной оптимизации, в рассматриваемом примере нелинейной является целевая функция, в диалоговом окне Параметры поиска решения не устанавливается флажок Линейная модель.
Корпоративные информационные системы Финансы и кредит |
8 |
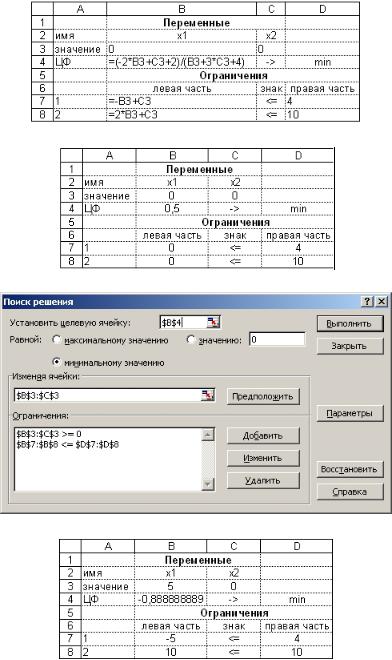
Электронная таблица в режиме отображения формул.
Электронная таблица в режиме отображения значений.
Параметры поиска решения.
Результат поиска решения.
Корпоративные информационные системы Финансы и кредит |
9 |

Самостоятельная работа
Найти оптимальное решение задачи.
Вариант 1
|
Задание 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
L(X) = 4x1 - 3x2 ® max (min) |
|
|
|
|
|
|
|
300x1 + 200x2 ® max |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
ì5x - 2x |
|
|
£ 20; |
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx |
|
£10; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ï |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
íx1 + 2x2 |
|
³10; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íx1 + 2x2 £16; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
ï |
|
+10x2 £ 80; |
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
î- 7x1 |
|
|
|
|
|
|
|
|
îx1 + x2 £12; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
x1 , x2 ³ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1, x2 |
³ 0, |
|
|
целые |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Задание 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
7x11 +11x12 + 7x13 + 4x21 +12x22 +18x23 ® min |
|
2x |
2 |
|
+ 3x |
2 + 4x x |
2 |
- |
6x |
|
- 3x |
2 |
® min |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|||||||
|
ìx + x |
|
|
+ x |
= 300; |
|
|
|
|
ìx11 + x21 £ 500; |
|
ìx |
|
+ x |
2 |
£ 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
£ 4; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
í |
11 |
12 |
|
|
13 |
|
|
|
|
|
|
íx12 + x22 £ 550; |
|
í2x |
+ |
3x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
îx21 + x22 |
|
+ x23 =1200; |
ïx |
|
+ x |
|
|
£ 550; |
î |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
23 |
|
x , x |
|
³ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î 13 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
xij |
³ 0, |
|
i =1,2, |
j = |
|
|
|
|
|
|
|
|
|
|
|
|
Ответ : x1 =1, x2 |
|
= 0, Z = -4. |
|
|
|
||||||||||||||||||||||||
|
|
1,3. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Вариант 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Задание 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
L(X) = 2x1 + 5x2 ® max (min) |
|
|
|
|
|
|
|
2x1 + 4x2 ® max |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
ì2x - x |
|
|
£ 6; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì3x + 4x |
|
|
£ 1700; |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
ï |
1 |
|
2 |
|
³ 5; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
í |
|
|
1 |
|
|
|
|
|
2 |
|
£ 9600. |
|
|
|
|
|
|
|
||||||||
|
ïx + 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12x + 30x |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
í |
1 |
|
2 |
|
£ 8; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î |
|
|
|
1 |
³ 0, |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
4x1 + x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x , x |
|
|
|
целые |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î- x1 + 2x2 ³ 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x1 , x2 ³ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Задание 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
4x11 + 6x12 + 2x13 + x21 + 9x22 + 7x23 |
|
® min |
|
x + |
2x |
2 |
|
- x |
2 ® max |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ìx + x |
|
|
+ x |
£ 150; |
|
|
|
|
ìx11 + x21 = 30; |
|
ì3x |
+ 2x |
2 |
£ 6; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
ï |
+ x22 |
= 90; |
|
íx |
|
1 |
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
í |
11 |
12 |
|
|
13 |
|
|
|
|
|
|
íx12 |
|
|
+ |
2 |
|
£ 4; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
îx21 + x22 |
|
+ x23 |
£ 100; |
|
|
|
|
ïx |
+ x |
|
|
=110; |
|
î |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
23 |
|
x |
, x |
|
³ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î 13 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xij |
³ 0, |
|
|
i = 1,2, |
j = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
2 |
|
|
|
4 |
|
||||||
|
|
|
1,3. |
|
|
|
|
|
|
|
|
Ответ : x1 |
|
=1 |
, |
x2 |
= |
, Z |
= |
2 |
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
3 |
9 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Корпоративные информационные системы Финансы и кредит |
10 |
