Reshenie-zadach-po-TOGI_2013

Министерство образования и науки Российской Федерации ФГБОУ ВПО Алтайский государственный технический университет им. И.И. Ползунова

Б.Ф. Азаров, И.В. Карелина

РЕШЕНИЕ ЗАДАЧ ПО ТЕОРИИ ОШИБОК

ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ

Методические указания для самостоятельной работы студентов, обучающихся по направлениям

270800 «Строительство» и 270100 «Архитектура»

Барнаул, 2013

1. ОСНОВНЫЕ ПРАВИЛА ГЕОДЕЗИЧЕСКИХ ВЫЧИСЛЕНИЙ. ВЫЧИСЛИТЕЛЬНЫЕ СРЕДСТВА

Вычисления – часть геодезических работ как при измерениях, так и при их обработке. Цель общих требований к вычислениям -

уменьшить вероятность совершения ошибки и получить результат наиболее простым способом. К таким требованиям относятся:

-Рациональная схема (алгоритм) вычислений - простота, нагляд-

ность, однотипность - для вычислений используют полевые журналы, специальные бланки, ведомости.

-Контроль вычислений:

а) текущий - проверяется правильность промежуточных вычислений;

б) заключительный - проверяется правильность окончательного результата.

- Независимые вычисления - «в две руки» (выполняются двумя вычислителями – каждым отдельно) и по контрольным формулам.

Требования к ведению записей:

вычисления размещают в таблицах или ведомостях;

написание цифр - аккуратное и четкое, исключающее неоднозначное прочтение;

записи чисел - столбиками разряд под разрядом;

количество десятичных знаков должно соответствовать правилам техники вычислений;

записи в таблицах и ведомостях не должны иметь исправлений;

в полевых журналах нельзя исправлять отсчеты «цифра по цифре»;

вычисления в журналах исправляют, зачеркивая неверные цифры и надписывая сверху верные;

все величины: приращения координат, превышения, невязки, углы наклона - пишут со своим знаком («+» или «-»).

Точные и приближенные числа.

Точные числа используют при счете отдельных предметов и понятий; например, масштабные коэффициенты или целые величины, условно присваиваемые границам физических интервалов.

Приближенные числа в геодезии получают, как правило, из измерений вместо точного.

3

Записанное приближенное число ошибочно не более, чем на половину единицы последнего разряда. Например: 4,785 - ошибочно на 0,0005; 4785 - ошибочно на 0,5 и т.д.

Вприближенных числах выделяют:

•десятичные знаки (все цифры числа, стоящие после запятой);

•значащие цифры (все цифры числа, кроме нулей слева);

•верные цифры (цифры, значение которых больше ошибки этого числа).

Примеры: 4,147 - 4 значащих цифры; 0,004147 - 4 значащих цифры; 40,00 - 4 значащих цифры;

217,35 м - 3 верных цифры при точности до метров (217). При вычислениях в числах удерживают такое количество знаков

и цифр, которое обеспечивает требуемую точность вычислений. Количество верных значащих цифр в результате операций сло-

жения, вычитания, умножения, деления, возведения в степень и извлечения корня определяется наименьшим количеством верных значащих цифр в исходных числах.

Правила округления:

•число значащих цифр промежуточных результатов берется больше числа верных цифр на 1-2 единицы последнего разряда,

•окончательный результат может содержать не более одной лишней значащей цифры.

Примеры: 3,4 0,4783 = 1,62622 ≈ 1,6;

98,763 - 45,8 + 0,7549 – 6,865 = 98,76 - 45,8 + 0,76 - 6,86 = 46,86 ≈ 46,9.

Округление приближенных чисел:

а) если первая отбрасываемая цифра больше 5, то последняя оставляемая цифра увеличивается на единицу: 2,46 ~ 2,5;

б) если первая отбрасываемая цифра меньше 5, то последняя оставляемая цифра не изменяется: 2,44 ~ 2,4;

в) если следующая после нечетной оставляемой цифры равна 5, то последняя оставляемая цифра округляется в большую сторону, если

Обработка результатов геодезических измерений требует достаточно больших объемов вычислений при сравнительно простых алго-

4

ритмах и высоким требованиям к оперативности и надежности получаемых результатов. Поэтому наиболее подходящими средствами для такого рода вычислений являются электронные микрокалькуляторы.

Электронные микрокалькуляторы подразделяются на программируемые и непрограммируемые, а по принципу выполнения вычислений – на микрокалькуляторы с алгебраической логикой вычислений

ис обратной бесскобочной логикой вычислений.

Вфункциональном отношении различия между разными видами микрокалькуляторов невелики. Ввод данных осуществляется цифровыми клавишами «0», «1», … «9» и клавишей десятичной точки «.». Микрокалькулятор может работать в нескольких режимах. Чаще всего используется основной режим и режим совмещенной функции. При работе калькулятора в основном режиме для обработки результатов геодезических измерений используют клавиши арифметических опе-

раций «+», «-», « », «÷», клавиши выполнения операций «=», смены знака числа «+/-», вычисления тригонометрических функций «sin», «cos», «tan», извлечения квадратного корня « 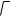», возведения в квад-

рат «х2», изменения представления аргумента тригонометрической функции «D R G» (соответственно, в градусах, радианах и градах), перевода угла, выраженного в ° ′ " в доли градуса «DEG», а также клавиши операций с памятью: «X→M» для записи в регистр памяти содержимого регистра индикации и «RM» или «М→Х» для вызова содержимого регистра памяти на табло, «М+» для алгебраического суммирования числа на табло с содержимым регистра памяти.

Перевод микрокалькулятора в режим совмещенной функции выполняется нажатием специальной клавиши («2ndF», «SHIFT» «F» и т.п.), при этом в верхнем левом углу табло (на индикаторе) воспроизводится соответствующий символ. Указанная клавиша обеспечивает выполнение функций, символы которых нанесены над клавишами функций основного режима работы микрокалькулятора. Для выполнения расчетов при обработке результатов геодезических вычислений чаще всего используются функция нахождения обратной величины «1/х», функция «π» ввода числа π, функция «DMS» перевода угла, выраженного в долях градуса, в ° ′ ", функции получения градусной меры угла по значениям функций sin, cos, tan, обозначенные символами «sin-1», «cos-1», «tan-1» над соответствующими клавишами тригонометрических функций. Фактически для обозначения функций arcsin, asccos, arctg использованы символы обратных тригонометрических функций, что некорректно с точки зрения математики.

5

2. ЗАДАЧИ ТЕОРИИ ОШИБОК. ВИДЫ ОШИБОК ИЗМЕРЕНИЙ

Измерения - важная часть геодезических работ; из них получают количественную информацию об объектах. В геодезии измеряют длины линий, горизонтальные и вертикальные углы, превышения.

Измерения бывают различного вида:

-непосредственные (прямые) измерения - когда мерный прибор, отображающий единицу измерения, непосредственно сравнивается с объектом измерения;

-посредственные (косвенные) измерения – когда искомая величина не измеряется, а получается вычислением по результатам измерений других величин.

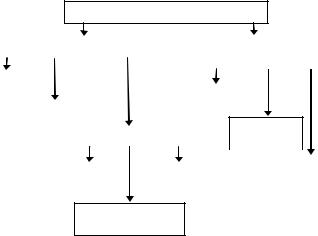
Результаты измерений (вычислений) содержат ошибки, величина которых зависит от прибора, применяемого при измерениях, способа измерения и вычислений конечных результатов. Классификация ошибок измерений приведена на рисунке 1.

ВИДЫ ОШИБОК ИЗМЕРЕНИЙ

ДЕЙСТВУЮЩИЕ

ПЕРИОДИЧЕСКИ

Рисунок 1 – Классификация ошибок измерений

Грубые ошибки – это результат промахов и просчетов. Их исключают при контроле измерений (например: линию на местности измеряют дважды – в прямом и обратном направлениях; горизонтальный угол измеряют при двух положениях вертикального круга – «круг лево» и «круг право» и т.п.).

6

Систематические ошибки возникают из-за неисправности приборов, одностороннего влияния условий внешней среды и т.п. Эти ошибки действуют по определенному математическому закону и могут быть вычислены до измерений.

Различают систематические ошибки:

•односторонне действующие, если у них знак постоянен, а величина меняется (например: поправка в отсчет за наклон нивелирной рейки);

•периодически действующие, если у них меняются и знак, и величина (например: поправка за эксцентриситет алидады горизонтального круга теодолита);

•постоянно действующие, если у них и знак, и величина постоянны (например: поправка за компарирование рулетки).

Систематические ошибки исключают из результатов измерений методикой измерений, введением поправок в результаты, исследованием и поверками приборов.

Случайные ошибки. Они неизбежно сопровождают измерения, причем их знак и величину до измерений точно предсказать невозможно. Случайные ошибки малы по величине и имеют разные знаки. Они зависят от:

•точности способа измерений,

•точности прибора,

•квалификации наблюдателя,

•внешних условий измерений.

Исключить случайные ошибки из результатов измерений нельзя, можно только их изучить, чем и занимается теория ошибок измере-

ний.

Теория ошибок геодезических измерений изучает:

•свойства ошибок и законы их распределения,

•методы обработки измерений с учетом их ошибок,

•способы получения числовых характеристик точности измерений.

Задачи теории ошибок, применительно к геодезии:

•нахождение наиболее надежного значения измеренной величины,

•оценка точности результатов измерений и их функций,

•установление допусков на использование результатов измерений.

3. СВОЙСТВА СЛУЧАЙНЫХ ОШИБОК ИЗМЕРЕНИЙ

Случайная истинная ошибка измерения - это разность между измеренным значением величины ℓ и ее истинным значением X, т.е.

7

= ℓ – X .

Свойства случайных ошибок:

1. Ограниченность: для данного вида и условий измерений абсолютные значения случайных ошибок не превосходят некоторого предела (допуска), т.е.

i ПРЕД . ,

где i = xi – X – абсолютное значение случайной ошибки; xi – результат измерений;

X – истинное значение измеряемой величины;ПРЕД. – предел (допуск).

2. Симметричность: при измерениях положительные и отрицательные случайные ошибки встречаются одинаково часто.

3. Плотность: малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.

4. Компенсированность: среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений, т.е.

lim 0 ,

n n

где [ ] - знак Гауссовой суммы; n – число измерений.

5. Рассеивание: предел отношения среднего арифметического из квадратов случайных ошибок не равен нулю, т.е.

lim 2 2 ,

n n

где σ – стандарт.

6. Пропорциональность: допуск пропорционален стандарту, т.е.

ПРЕД const .

8

Если ошибки ряда измерений обладают свойствами с 1 по 6, то их считают случайными.

4. ПОНЯТИЕ О КРИТЕРИЯХ ДЛЯ ОЦЕНКИ ТОЧНОСТИ ИЗМЕРЕНИЙ

Точность измерений – их качество, определяющее близость результатов измерений к точному значению измеряемой величины.

Точное значение измеряемой физической величины, если оно не определяется теоретически, неизвестно. В отдельных случаях за точное значение величины может быть принято ее измеренное значение, максимально близкое к истинному значению. В геодезии такие величины называют действительными или исходными.

Имея значения i истинных или случайных ошибок результатов измерений одной и той же величины, можно получить следующие ко-

личественные характеристики точности измерений:

• θ – средняя ошибка, т.е. среднее арифметическое из абсолютных значений ошибок

где i = 1, 2,…, n; n – число измерений.

• r - вероятная (срединная) ошибка – такая, которая находится в середине ряда ошибок, расположенных в порядке возрастания или убывания по абсолютному значению.

Кроме того, к критериям точности измерений относятся:

• σ – стандарт (основная мера точности результатов геодезических измерений):

а) σ определяет величину рассеивания (разброса) отдельных случайных ошибок относительно их среднего арифметического;

б) предельное значение случайной ошибки ПРЕД. пропорционально стандарту σ.

• m – средняя квадратическая ошибка (СКО).

В геодезии понятие СКО было введено Гауссом; он же разработал основные положения теории ошибок.

На практике при ограниченном числе измерений n СКО одного измерения m вычисляется по формуле Гаусса

9

где 2 21 22 23 2n .

Для характеристики точности измерений недостаточно указать СКО, также важно установить - по какому числу измерений получено ее значение, т.е. необходимо определить СКО самой СКО

mm m . 2n

Фактически величина mm позволяет количественно оценить точность замены стандарта на СКО.

считается надежной, если mm 0,25m. Это условие выполнимо при n 8. Минимальное число наблюдений для надежной оценки точности n = 8.

Между количественными характеристиками точности геодезических измерений существуют следующие зависимости, которые часто используют на практике:

1) Связь средней θ и вероятной (срединной) r ошибок со стан-

2) Связь средней квадратической ошибки m со средней θ и вероятной (срединной) r ошибками

Величина предельной ошибки зависит от степени ответственности измерений. В качестве служебного допуска принимают ПРЕД 2m, для теоретических расчетов ПРЕД 3m.

Относительная ошибка - это отношение абсолютной ошибки к измеренной величине X, т.е.

10