1 Детерминированный факторный анализ, область применения, типы моделей

Детерминированный фактор­ный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер.

С помо­щью детерминированных факторных моделей исследуется функ­циональная связь между результативным показателем (функцией) и факторами (аргументами).

При создании детерминированных факторных моделей необ­ходимо выполнять ряд требований:

1. факторы, включаемые в модель, должны реально существо­вать, а не быть надуманными абстрактными величинами или яв­лениями;

факторы, входящие в модель, должны находиться в причин­но-следственной связи с изучаемым показателем. Факторные мо дели, которые отражают причинно-следственные отношения меж­ду показателями, имеют значительно большее познавательное значение, чем модели, созданные при помощи приемов математи­ческой абстракции. Последнее можно проиллюстрировать следу­ющим образом. Возьмем две модели:

ВП = ЧР * ГВ;

Г В = ВП: ЧР,

где ВП — валовой выпуск продукции предприятия; ЧР— численность работников на предприятии; ГВ — среднегодовая выработка продукции одним работни­ком. В первой модели факторы находятся в причинной связи с ре­зультативным показателем, а во второй — в математическом соот­ношении. Значит, вторая модель, построенная на чисто математи­ческих зависимостях, имеет меньшую познавательную и практи­ческую ценность, чем первая;

3. все показатели факторной модели должны быть количе­ственно измеримыми, т.е. иметь единицу измерения и необходи­мую информационную базу;

4. факторная модель должна обеспечивать возможность изме­рения влияния отдельных факторов, т.е. в ней должна учитываться соразмерность изменений результативного и факторных показате­лей, а сумма влияния отдельных факторов должна равняться об­щему приросту результативного показателя.

В детерминированном анализе выделяют следующие типы наи­более часто встречающихся факторных моделей.

1. Аддитивные модели:

Y = =х_]+х₂ + ... + х_n

Они используются в тех случаях, когда результативный показа­тель представляет собой алгебраическую сумму нескольких фак­торных показателей.

2. Мультипликативные модели:

Этот тип моделей применяется в том случае, когда результатив­ный показатель представляет собой произведение нескольких фак­торных показателей.

3. Кратные модели:

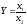
Они применяются в том случае, когда результативный показа­тель получают делением одного факторного показателя на величи­ну другого.

1. Смешанные (комбинированные) модели — сочетание в различ­ных комбинациях предыдущих моделей:

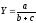
Y=(a+b)c и т.д.

2. Метод цепных подстановок, область применения, способы расчета

Наиболее универсальным является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах де­терминированных факторных моделей: аддитивных, мультипли­кативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме ре­зультативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и последующих факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изме­нения уровня определенного фактора позволяет элиминировать влияние всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.

Порядок применения этого способа рассмотрим на примере (табл. 5.1).

Как уже известно, объем выпуска продукции (ВП) зависит от двух основных факторов первого уровня: численности рабочих

Таблица 5.1

Данные для факторного анализа объема выпуска продукции

	Показатель	Услов­ное обозна­чение	Значение показателя		Изменение
			tо	ti	абсо­лютное	относи­тельное, %
	Выпуск продукции, млн руб.	ВП	400	600	+ 150	+50
	Среднесписочная численность рабочих, человек	ЧР	100	120	+20	+20
	Количество отработанных дней всеми рабочими за год	D	20 000	25 000	+5000	+25
	Количествоотработанныхчасов всеми рабочими за год	t	160 000	187 500	+27 500	+ 17,2
	Среднегодовая выработка про­дукции одним рабочим, млн руб.	ГВ	4	5	+ 1	+25
	Количество отработанных дней одним рабочим за год	Д	200	208,33	+8,33	+4,17
	Среднедневная выработка рабочего, тыс. руб.	ДВ	20	24	+4	+20
	Средняя продолжительность смены,ч	п	8	7,5	-0,5	-5
	Среднечасовая выработка про­дукции одним рабочим, тыс. руб.	чв	* 2,5	3,2	+0,7	+28

Примечание: t₀ — базисный уровень показателя, в качестве которого может быть прошлый период, план отчетного периода, другое предприятие и т.д.; t_] — текущий уровень показателя.

(ЧР) и среднегодовой выработки (ГВ). Имеем двухфакторную мультипликативную модель:

ВП=ЧР ГВ.

Алгоритм расчета способом цепной подстановки для этой мо­дели:

ВП₀=ЧР₀*ГВ₀=100*4=400 млн руб

ВП_усл=ЧР₁*ГВ₀=120*4=480 млн руб

ВП₁=ЧР₁*ГВ₁=120*5=600 млн руб

Как видим, второй показатель ВП отличается от первого тем, что при его расчете принята численность рабочих отчетного пери­ода вместо базисного. Среднегодовая выработка продукции одним рабочим в том и другом случае базисная. Значит, за счет роста численности рабочих выпуск продукции увеличился на 80 млн руб. (480-400).

Третий показатель ВП отличается от второго тем, что при рас­чете его величины выработка рабочих принята по уровню отчетно­го периода вместо базисного. Количество же работников в обоих случаях — отчетного периода. Отсюда за счет повышения произ­водительности труда объем выпуска продукции увеличился на 120 млн. руб. (600-480).

Таким образом, изменение объема выпуска продукции явилось результатом влияния следующих факторов:

а)увеличения численности рабочих + 80 млн. руб.

б)повышения уровня производительности труда + 120 млн. руб.

Итого + 200 млн. руб.

Алгебраическая сумма влияния факторов обязательно должна быть равна общему приросту результативного показателя:

АВП_чр + АВП_ГВ=АВП_о6щ.

Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах.

Для наглядности результаты анализа приведены в табл. 5.2.

Таблица 5.2

Результаты факторного анализа валового выпуска продукции

Показа­тель	Численность рабочих		Годовая выра­ботка рабоче­го, млн руб.			Выпуск продукции, млн руб.				Изменение объема выпуска продукции, млн руб.
	'о	ч	to	Ч	'о		уел".	ч	общее		В том числе за счет
											чис­лен­ности рабо­чих	годо­вой выра­ботки
Цех1	50	52	4,5	5,5	225		234	286	+61		+9	+52
Цех 2	35	40	3,8	4,8	133		152	192	+59		+ 19	+40
И Т.Д.
Всего	100	120	4,0	5,0	400		480	600	+200		+80	+ 120

Выпуск продукции при численности рабочих отчетного периода и годовой выработке базисного периода.

Если требуется определить влияние четырех факторов, то рас­считываются три условных показателя вместо одного; т.е. количество условных величин результативного показателя на единицу меньше числа факторов.

Проиллюстрируем это на четырехфакторной модели валового выпуска продукции:

ВП = ЧР*Д*П*ЧВ.

Исходные данные для решения задачи приведены в табл. 5.1:

ВП₀ =ЧР₀-Д₀-П₀-ЧВ₀= ,

= 100 • 200* 8 * 2,5 = 400 млн руб.; '

_ВПусл1 = ЧР₁* Д₀ *П₀ *ЧВ₀ =

= 120 * 200 * 8 * 2,5 = 480 млн руб.;

вп_усл2=чр_1*д_1*п_1*чв₀=

= 120 * 208,3 -8-2,5 = 500 млн руб.; =

ВП_усл3=ЧР₁*Д₁*П₁*ЧВ₀=

= 120 * 208,3 * 7,5 * 2,5 = 468,75 млн руб.;

ВП₁=ЧР₁*Д₁*П₁*ЧВ₁=

= 120 * 208,3 - 7,5 - 3,2 = 600 млн руб.

Выпуск продукции в целом увеличился на 200 млн руб. (600 - 400), в том числе за счет изменения:

а) количества рабочих:

ΔВП_ЧР= ВП_усл] - ВП₀ = 480 - 400 = +80 млн руб.;

б) количества отработанных дней одним рабочим за год:

ΔВП_Д = ВП_усл2 - ВП_усл1 = 500 - 480 = +20 млн руб.;

в) средней продолжительности рабочего дня:

ΔВП_П = ВП_усл3 - ВП_усл2 = 468,75 - 500 = -31,25 млн руб.;

г) среднечасовой выработки:

ΔВП_ЧВ = ВП₁ - ВП_ул3ъ = 600 - 468,75 = +131,25 млн руб.

Итого +200 млн руб.

^: Применяя способ цепной подстановки, необходимо знать пра­вила последовательности расчетов: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько качествен­ных показателей, то сначала следует изменить величину факторов первого уровня подчинения, а потом более низкого) В приведенном⁴ примере объем производства продукции зависит of четырех факто­ров: количества рабочих, количества отработанных дней одним рабочим, продолжительности рабочего дня и среднечасовой выра­ботки. Согласно рис. 3.5 количество рабочих по отношению к валовому выпуску продукции — фактор первого уровня, количество! отработанных дней — второго уровня, продолжительность рабочего дня и среднечасовая выработка — факторы третьего уровня/Это и обусловило последовательность размещения факторов в модели и, соответственно, очередность определения их влияния.

Таким образом, применение способа цепной подстановки тре­бует знания взаимосвязи факторов, их соподчиненное™, умения правильно их классифицировать и систематизировать.;

Мы рассмотрели пример расчета влияния факторов на прирост результативного показателя в мультипликативных моделях.

- В кратных моделях алгоритм расчета факторов на величину ис­следуемых показателей следующий:

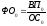
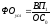
Общее изменение уровня фондоотдачи

Δфо_о6щ = фо₁-фо₀.

В том числе за счет:

• объема производства продукции:

ΔФО_вп = ФО_усл-ФО₀;

• суммы основных средств:

ΔФ0_ос = ФО₁ –ФО усл где ФО — фондоотдача;

ОС — среднегодовая стоимость основных средств производ­ства.

Методика расчета влияния факторов в смешанных моделях ад­дитивно-мультипликативного вида:

а)типа П= VРПo(Ц-С):

П₀=VРП₀-(Ц₀-С₀);

Пусл1=VРП1*(Ц0-С0)

Пусл2=VРП2*(Ц0-С0)

П1=VРП1*(Ц0-С0)

ΔП_общ=П₁-П₀

ΔП_VРП=П_усл1-П₀ ΔП_Ц=П_усл2-П_усл1 ΔП_С=П-П_усл2

где П — сумма прибыли от реализации продукции;

VРП— объем реализации продукции в натуральном измере­нии;

Ц — цена единицы продукции;С — себестоимость единицы продукции;

б) типа

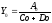
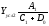
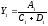
Аналогичным образом рассчитывают влияние факторов и по другим детерминированным моделям смешанного типа.

Отдельно необходимо остановиться на(методике определения влияния структурного фактора с помощью способа цепной подстановки) Методику этого расчета рассмотрим на примере выручки от реализации продукции (В), которая во многом зависит не только от цены (Ц) и количества проданной продукции {VJPJ1), но и от ее структуры (.Удi) Если возрастет доля продукции высшей категории качества, которая продается по более высоким ценам, то выручка за счет этого увеличится, и наоборот. Факторная модель этого показателя может быть записана так:

В=VРП_общ*Удi*Цi

В процессе анализа необходимо элиминироваться от воздей­ствия всех факторов, кроме структуры продукции. Для этого срав­ниваем следующие показатели выручки:

Вусл1=VРПобщ1*Удio*Цio

Разность между этими показателями учитывает изменение вы­ ручки только за счет изменения структуры или сортового состава продукции (табл. 5.3).

Таблица 5.3

Расчет влияния структурного фактора на изменение выручки от реализации продукции способом цепной подстановки

Сорт продукции	Цена 1т, тысруб.	Объем про­даж, т			Структура продаж			Объем продаж отчетного периода при базисной его структуре, т		Выручка в млн руб. за VPH] при структуре
				to		'			t		T1
1-й	2700	180 '	200	0,9		0,8	225		607,5		540
2-й	2300	20	50	0,1		0,2	25		57,5		115
Итого		200	f 250	1,0		1,0	250		665,0		655

Из таблицы видно, что с увеличением удельного веса продукции второго сорта в общем объеме ее реализации выручка уменьшилась на 10 млн. руб. (655 - 665). Это можно расценивать как неиспользованный резерв предприятия.